Расчет нестационарного температурного поля однослойной вертикальной ограждающей конструкции здания методом конечных разностей при граничных условиях третьего рода, страница 3

Рассмотрим наиболее простой случай ввода граничных условий I и III родов для полуограниченного тела, применительно к задаче, поставленной в данной работе.

Предположим, что на поверхности полуограниченного тела задана температура Т_п, одинаковая по всей площади и постоянная во времени. Начальные условия, т.е. температура рассматриваемого объема, в начальный момент времени задана одинаковой по всему объему (рис.2).

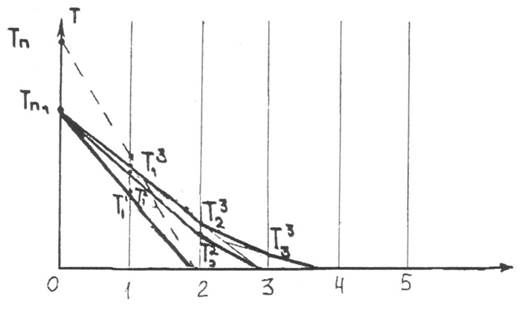
Рис.2. Ввод граничных условий I рода

Разобьем тело на n слоев ∆X (0,1,2,3,...). Следуя правилу графического определения температур в K+I момент времени для сечения I, соединим точку в сечении 0 с ординатой Т и в сечении 2 с ординатой Т₀. В месте пересечения прямой линии с ординатой сечения I найдем искомую температуру T₁^k+1. Сравнивая полученный результат с точным аналитическим решением этой задачи, например, по выражению (7), можно убедиться, что значение величины при точном решении находится на 1/3 ниже полученной нами точки, т.е. для получения более правильного решения задачи в начальный момент времени, целесообразно производить графическое построение при нахождении температур в сечении I, используя точку T_n1, расположенную в сечении - О и имеющую ординату .

Несколько иначе производится ввод граничных условий III рода. Разобьем, как и ранее, фрагмент полуограниченного тела на слои толщиной ∆Х, а также введем эквивалентный слой, расположенный за пределами тела в сторону окружающей среды. Эквивалентный слой вводится для замены переноса энергии путем конвективного теплообмена перекосом энергии за счет теплопроводности. Толщина эквивалентного слоя определяется из условия равенства его термического сопротивления теплопроводности заданному сопротивлению конвективного теплообмена на поверхности тела, по выражению:

Отсюда , где  - толщина эквивалентного слоя.

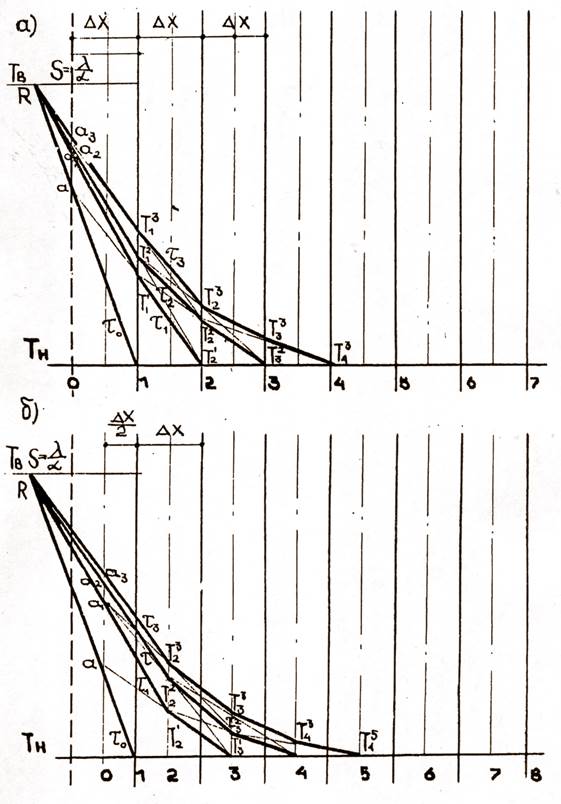
Температура среды в этом случае задается как температура на границе эквивалентного слоя (точка R), т.е. на его поверхности при граничных условиях1-го рода (рис.3, а). При этом следует помнить, что эквивалентный слой не имеет массы и теплоемкости, т.е. Сρ=0.

Построение начинаем с нахождения температурной кривой в момент времени τ=0. (рис.3а). Для этого соединим точки R с точкой I, полученная ломаная R,1,2,3,4... и определяет начальные температурные условия. Границу слоя, который откладываем на расстоянии Δх от поверхности тела, используем для нахождения температур в момент времени τ+1 в сечении О.

Точки пересечения прямых линий, соединяющих точку R с точками, определяющими величины температур в сечении О, будем обозначать как а₁,а₂,а₃… Тогда ломаная R, а_т, 1,2,3... даст нам картину распределения температур в момент времени τ+1.

Сравнение полученного результата с точным аналитическим решением убеждает нас в том, что используемый метод ввода граничных, условий дает погрешность в определении температурного поля в первый промежуток времени. Более точно температурное поле можно определить, если находить значения температур по сечениям тела не для границ слоев, а для их осей. В этом случае ломаные линии температур имеют вид (рис.3, б).

Точность построения температурного поля может быть проверена при определении теплового баланса прихода и расхода тепла ограждающей конструкции в любой К-тый момент времени τ.

                                                     (9)

где q_в^к — удельный поток тепла, переданный поверхности ограждения от внутреннего воздуха, Вт/м²;

q_а^к— удельный поток тепла, аккумулированный ограждающей конструкцией, Вт/м²;

q_н^к— удельный поток тепла, отданного поверхностью ограждения наружному воздуху, Вт/м².

3.Методические указания

1.  На  основании условия  задания     сформулировать   задачу  работы, в   которой  должны  быть   отражены  следующие  вопросы:

а)           Рассчитывается  процесс  нагрева  или  охлаждения.