Определение разности давлений в точках нефтяных резервуаров, составление уравнения равновесия относительно плоскости равного давления

Министерство образования Республики Беларусь

Белорусский Национальный Технический Университет

Кафедра «Гидралика»

Расчётно-графическая работа

                                             Выполнила: 

      студентка гр.

                                           

                                           Проверил:

                                                                    

Минск-2010

ЗАДАЧА № 1.12

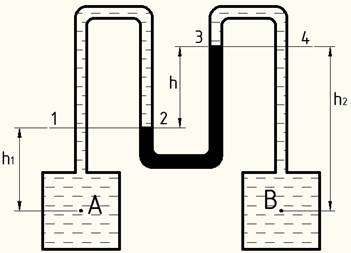
К двум резервуарам А и В, заполненным нефтью, присоединён дифференциальный ртутный манометр. Определить  разность давлений в точках А и В, составив уравнение равновесия относительно плоскости равного давления. Разность показаний дифманометра h=0,25 м.

Данные из справочников:

ρ_н = 800 кг/м³

ρ_рт = 13600 кг/м³

Решение

Жидкость в дифманометре находится в равновесии, поэтому давление в точке 1 равно давлению в точке 2 (как давления в точках однородной жидкости, расположенных в горизонтальной плоскости), т.е.             р₁ = р₂  (аналогично рассуждая р₃ = р₄).

Из рисунка видно: р_А = р₁ + ρ_н·g·h₁ ; р_В = р₄ + ρ_н·g·h₂ ; р₁ = р₄ + ρ_рт·g·h, где ρ_рт – плотность ртути,

ρ_н – плотность нефти.

Разность давлений в точках А и В, р_А - р_В = р₁ + ρ_н·g·h₁ - р₄ - ρ_н·g·h₂ = (р₁ - р₄) - ρ_н·g·( h₂ - h₁) =

= (р₁ - р₄) - ρ_н·g·h = (р₄ + ρ_рт·g·h - р₄) - ρ_н·g·h = g·h·(ρ_рт - ρ_н), р_А - р_В = 0,25·9,81·(13600 - 800) = 31392 Па = 0,32 атм.

Ответ:р_А - р_В = 0,032 атм.

ЗАДАЧА № 2.12

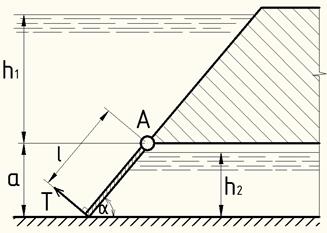Определить начальное подъемное усилие T, необходимое для открытия прямоугольного затвора АВ  при линейных размерах:

a=1,6 м; b=2 м; h₁=2,8 м; h₂=1,4 м, если масса затвора М=120 кг и его угол наклона к горизонту α=50°. Трением в шарнире пренебречь. Расчет выполнить аналитическим и графоаналитическим способами. Плотность жидкости ρ=10³ кг/м³.

Аналитическое решение

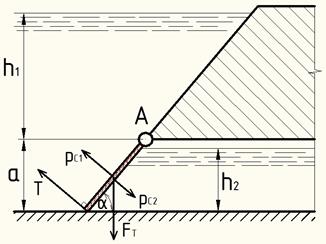
Сила полного гидростатического давления, действующая на затвор слева:       р₁ = р_с1·S₁  , где р_с1 – гидростатич. давление столба жидкости слева затвора; 

S₁ – площадь, на которую действует давление р_с1.

р₁ = ρg(h₁ +) ·b·  = 1000·9,81·(2,8+1,6/2) ·2·1,6/ = 147525,64 Н

Справа затвора: р₂ = р_с2·S₂ = ρg(h₂/2) ·b·  = 1000·9,81·(1,4/2) ·2· = 25099,85 Н

Сила тяжести затвора: F_T = Mg = 120·9,81 = 1177,2 Н

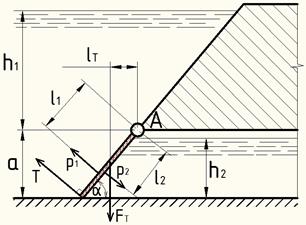Найдём расстояние от шарнира А до центров приложения сил давления и силы тяжести соответственно:

₁ = =  = 1,39 м    [1, с.39]

₂ =  +  =  +  = 1,48 м

 =  =  = 0,67 м

Составим уравнение моментов всех сил относительно шарнира А:

М_А = – р₁·₁ + р₂·₂ - F_T · + T · = 0,  где   =  =  = 2,09 м

Т =  =  = 80,72 кН

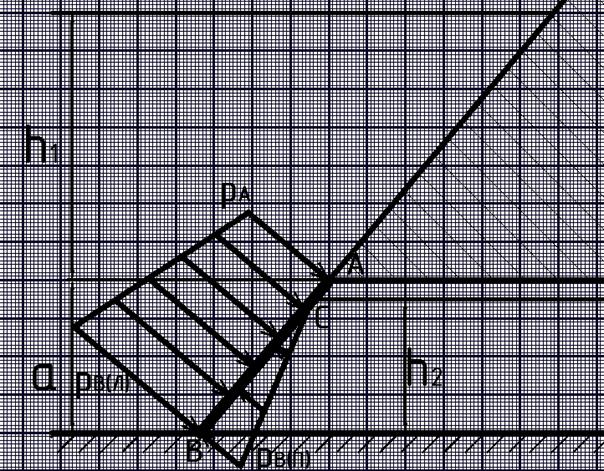Графическое решение

Давления слева затвора по эпюре:

р_А = ρgh₁ = 1000·9,81·2,8 = 27468 Па р_B(Л) = ρg·(h₁ + 𝑎 ) = 1000·9,81·(2,8 + 1,6) = 43164 Па

Давления справа затвора по эпюре:

р_С = 0

р_B(П) = ρgh₂ = 1000·9,81·1,4 = 13734 Па

Сила давления слева:

р₁= · (р_А + р_B(Л))··b =  ·(р_А + р_B(Л))· · b =

=   · (27468 + 43164)· ·2 = 147525,64 Н

Сила давления справа:

р₂= · р_B(П) ·  · b =   · 13734· ·2 = 25099,85Н

Ответ: Т = 80,72 кН

ЗАДАЧА № 3.12

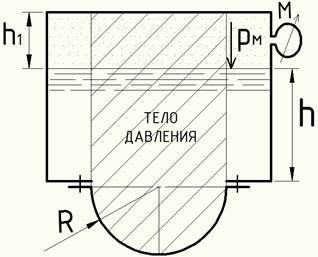
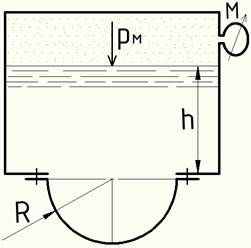Определить растягивающее усилие, воспринимаемое болтами полусферической, крышки бензорезервуара, если показание манометра р_м=39,24 кПа, радиус крышки R=4,8 м  и плотность бензина ρ₀ = 700 кг/м³. Высота уровня бензина h=3,4 м.

Решение

Из рисунка выше находим растягивающее усилие крышки бензорезервуара:

P = ρ₀gW  ,  W = πR²· (h + h₁) + πR³ ,  h₁ =   , где W – объём тела давления.

P = ρ₀g·[ πR²· (h +   ) + πR³ ]

P = 700·9,81·[π·4,8²·(3,4+ ) + ·π·4,8³] = 6,12 МПа = 62,4 атм

Ответ: P = 62,4 атм

ЗАДАЧА № 4.12

Определить минимальное значение силы F₁ приложенной к штоку, под действием которой начнется движение поршня диаметром D=100 мм, если сила пружины, прижимающая клапан к седлу, равна F_п=135 Н, а давление жидкости за клапаном р₂=0,16 МПа. Диаметр входного отверстия (седла) клапана d₁ = 10 мм. Диаметр штока d=50 мм, давление жидкости в штоковой полости гидроцилиндра р₁=1,4 МПа.

Силами трения пренебречь.

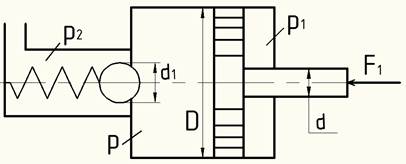
Решение

Рассмотрим силы, действующие на неподвижный клапан:

р₂· + F_п = p·, где  и  – площадь седла и поршня соответственно.

Рассмотрим силы, действующие на неподвижный поршень:

p· = F₁ + p₁· , где  – площадь поршня в штоковой полости гидроцилиндра, на которую действует давление р₁.

Приравнивая левую правую части выражений выше, получаем:

р₂· + F_п = F₁ + p₁·

F₁ = р₂· + F_п – p₁·

F₁ = 0,16·10⁶ ·  + 135 – 1,4·10⁶· = –2601 Н

Ответ:F₁ = – 2601 Н

ЗАДАЧА № 5.12

Заполнение бака бензином происходит через воронку диаметром

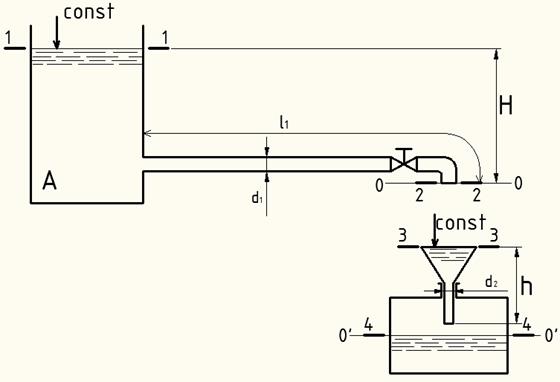d₂ = 50 мм, высотой h = 400 мм  с   коэффициентом  сопротивления ζ_в = 0,25. Определить, какой наибольший напор Н можно иметь в резервуаре А, чтобы воронка не переполнялась, и каков при этом расход бензина, поступающего в бак. Трубы стальные новые диаметром d₁ = 40 мм и длиной  ₁ = 40 м, угол открытия крана α = 30°, температура бензина 20°С.

Данные из справочников:

ζ_кр = 5,47 [5, c.94];    ρ_Б = 710 кг/м³;   ∆ = 0,06 мм [2, c.56]

ν_Б = 0,88·10^-6 м²/с [2, c.226]

Решение

Уравнение Бернулли для сечений 3 и 4 относительно плоскости 0’:

z₃ +    +  = z₄ +    +  + Σh_тр2

z₃ = h            = р_атм V₃ = 0

z₄ = 0            = р_атм V₄ = V’     Пусть α = 1 (турбулентное движение)

h =  + Σh_тр2 =  + ζ_в·  + λ₂ · ;

h =  · (1+ ζ_в + λ₂ );

Пусть λ₂ = 0,11·()^0,25 = 0,11· ()^0,25 = 0,02

V’ = 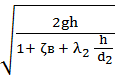 =  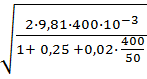= 2,36 м/с

Проверка допущений: Re =  =  = 134091

20  < 134091 < 500  (переходный режим течения)

Значит, λ₂ = 0,11·()^0,25 = 0,11· ()^0,25 = 0,022

V’ = 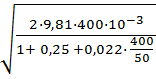 = 2,35 м/с

Re =  =  = 133523

20  < 133523 < 500  (переходный режим течения) →  α = 1

Q = V’· ω₂ = V’·  = 2,35· = 0,0046 м³/с = 4,6 л/с

Уравнение наразрывности: Q = Q₁

Q = V·ω₁;  V = =  = 3,66 м/с

---------------------------------------------------------------------------------Уравнение Бернулли для сечений 1 и 2 относительно плоскости 0:

z₁ +    +  = z₂ +    +  + Σh_тр1

z₁ = H            = р_атм         V₁ = 0

z₂ = 0            = р_атм         V₂ = V     Пусть α = 1 (турбулентное движение)

H =  + Σh_тр1 =  + ζ_кр·  + λ₁ ·  =  · (1+ ζ_кр + λ₁ );

Re =  =  = 166364

20  < 166364 < 500  (переходный режим течения) →  α = 1

λ₁ = 0,11·()^0,25 = 0,11· ()^0,25 = 0,023

H= · (1+ 5,47 + 0,023·) = 20,12 м.

Ответ: Q = 4,6 л/с ;  H = 20,12 м.

ЗАДАЧА № 6.12

Определить время опорожнения составного цилиндрического резервуара с водой размерами D₁ = 1м, D₂ = 2 м, H₁ = 3,2 м, H₂ = 4м через вертикальную трубу высотой h = 3 м и диаметром d = 0,0175 м  при открытом вентиле с коэффициентом сопротивления ζ = 5. Коэффициент сопротивления трения в трубе принять равным  λ = 0,03.

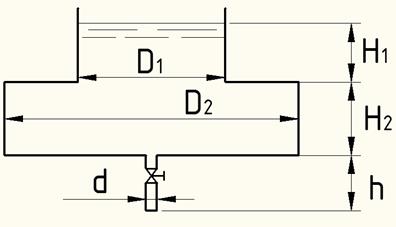Решение

Время истечения при переменном напоре:  

t = =  [2, с.152], где σ – площадь горизонтального сечения резервуара;

ω – площадь отверстия;

μ – коэффициент расхода отверстия;

W – объём жидк. над выходным сечением;

H – напор над центром тяжести выходного отверстия.

H=H₁+H₂+h=3,2+4+3=10,2 м

W=  · ( · H₁ +  · H₂) =  · (1² · 3,2 + 2² · 4) = 15,08 м³

μ = 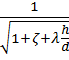 =  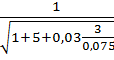 = 0,373 [2, с.151],

ω =  =  = 0,0044 м²

t =  = 1299 с

Ответ:t= 1299 с

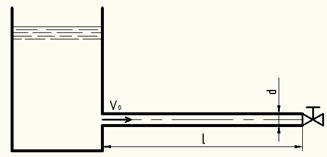
ЗАДАЧА № 7.12

В результате закрытия задвижки за время t_з=6 c на конце трубопровода диаметром d=125 мм и длиной=1200 м произошло повышение давления на ∆р=196,2 кПа. Определить начальную скорость V0 движения воды в трубопроводе, если толщина его стенок δ=10 мм. Материал трубопровода – чугун. 

 Данные из справочников:

Е = 2·10⁹ Па [2, c.6]

Е_чуг = 11,5·10¹⁰ Па [2,c.230, прил.10]

ρ = 10³ кг/м³

Решение

Скорость распространения ударной волны в трубопроводе:                                              

𝑎 = ·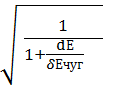, где

Е – модуль упругости жидкости, Па;

Е_чуг – модуль упругости материала стенки трубы, Па;

ρ – плотность жидкости (воды), кг/м³;

d – диаметр трубы, м;

δ – толщина стенки трубы, м.

𝑎 =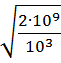 ·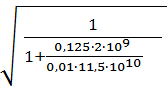= 1281,74 м/с.

Время, в течение которого возникшая у задвижки ударная волна достигнет резервуара и, отразившись от него, снова пойдёт к задвижке:

== 1,87 с.

Т.к. < t_з, то давление не достигает максимальной величины, потому что частично погашается отражённой волной, поэтому гидравлический удар является непрямым. В этом случае повышение давления рассчитывается по формуле Мишо: ∆р = 2ρV0 /  t_з .

V0 = t_з·∆р / (2ρ= 6·196,2·10³/(2·10³·1200) = 0,49 м/с.

Ответ:V0 =0,49 м/с.

ЗАДАЧА № 8.12

Определить отметку уровня воды в водонапорной башне s^А, необходимую для пропуска по трубопроводу  с параллельным и последовательным соединением труб расходов Q_п1 = 6 л/с, Q_B = 9 л/с, Q_C = 8 л/с, Q_D = 5 л/с,  при их размерах

 ₁ = 210 м,  ₂ = 160 м,  ₃ = 240,  ₄ = 210, d₁ = 150 мм, d₂ = 125 мм, d₃ = 100 мм, d₄ = 100 мм, если трубы новые чугунные, отметка трубопровода в точке D равна s^D = 6 м.

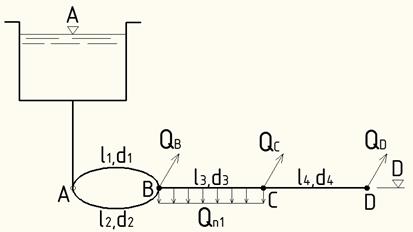Решение

h = 𝜃₂·,

где 𝜃₂ – поправочный коэффициент (из справочника)

k² – расходная характеристика (из справочника по диаметру