6.11. Расчет режима сетей с равномерно распределенной нагрузкой
В некоторых электрических сетях, например, например, в сетях уличного освещения, участков цехов с одинаковым оборудованием и равномерно расположенным по длине цеха , можно выделить часть сети с равномерно распределенной нагрузкой (рис.6.17).
Рассмотрим расчет режима,
например кабельной линии с равномерно распределенной по всей длине нагрузкой
(рис.6.17,а), в которой можно пренебречь индуктивным сопротивлением. При
отсутствии его на потерю напряжения в линии не влияет реактивная мощность
нагрузки. Расчету потери напряжения в такой линии эквивалентен расчет воздушной
линии с равномерно распределенной чисто активной нагрузкой. В обоих этих
случаях реактивная составляющая потери напряжения ![]() равна нулю либо из-за неучета индуктивного сопротивления,
либо из-за отсутствия реактивной мощности
равна нулю либо из-за неучета индуктивного сопротивления,
либо из-за отсутствия реактивной мощности
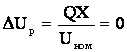 .
.
Таким образом для данных случаев расчетная схема может быть представлена только активной нагрузкой и активным сопротивлением линии.
Обозначим через р удельную активную мощность нагрузки единицы длины линии. Тогда суммарная для элемента длины dl мощность нагрузки равна pdl, а суммарная активная мощность Р всей линии длиной L будет равна
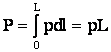 .
(6.82)
.
(6.82)
Суммарная мощность Р течет
в самом начале линии. Чем дальше от начала линии, тем меньше протекающая по ней
мощность. Потеря напряжения, вызываемая мощностью pdl, проходящей по участку длиной l с сопротивлением ![]() будет равна
будет равна
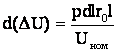 ,
,
где ![]() - удельное активное сопротивление
линии.
- удельное активное сопротивление
линии.
Потеря напряжения, вызываемая всей равномерно распределенной нагрузкой на длине L
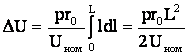 .
.
С учетом формулы (6.82) имеем
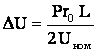 . (6.83)
. (6.83)
Известно, что для линии длиной L с сосредоточенной активной нагрузкой Р в конце ее
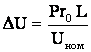 .
.
Сравнивая эту формулу с выражением (6.83) видим, что при определении потери напряжения в линии с равномерно распределенной активной нагрузкой р, ее можно заменить суммарной сосредоточенной нагрузкой Р , приложенной в середине рассматриваемой линии L/2.
На основе аналогичных рассуждений и выкладок можно получить формулу расчета потери напряжения в линии с равномерно распределенной чисто реактивной нагрузкой
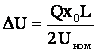 , (6.84)
, (6.84)
где Q - суммарная сосредоточенная реактивная мощность, вычисленная по удельной реактивной мощности q (Q=qL);
![]() - удельное реактивное сопротивление линии.
- удельное реактивное сопротивление линии.
И, наконец, используя выражение (6.83) и (6.84) можно получить формулу расчета потери напряжения для общего случая линии с равномерно распределенной активной и реактивной нагрузкой
 . (6.85)
. (6.85)
Для линии с равномерно распределенной нагрузкой на части длины линии (рис. 6.17,б) формулы расчета потери напряжения (6.83) и (6.85) получают соответственно следующий вид
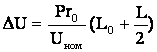 ; (6.86)
; (6.86)
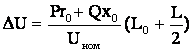 . (6.87)
. (6.87)
Потери мощности в элементе длины dl линии, расположенном на расстоянии l от начала линии равны
![]()
Проинтегрировав это выражение от 0 до L, получим потери мощности во всей линии:
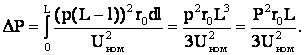
Для линий длиной L с сосредоточенной активной нагрузкой Р, приложенной в ее конце, потери мощности
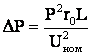 .
.
Таким образом, при расчете потерь мощности линию с равномерно распределенной нагрузкой p можно заменить суммарной сосредоточенной нагрузкой Р, приложенной на расстоянии 1/3 от начала линии.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.