Включение цепи RL на постоянное напряжение

Включение цепи RL на постоянное напряжение

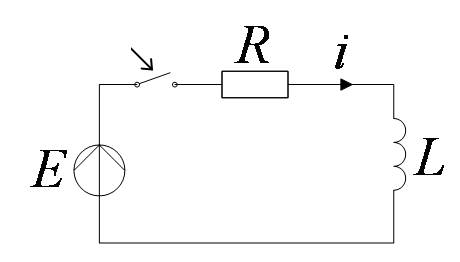
Для момента времени 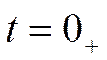 уравнение по 2-му закону Кирхгофа

u_R+u_L=E

или в интегрально-дифференциальной форме

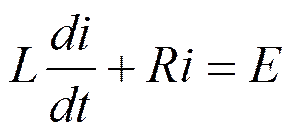
Решение однородного уравнения

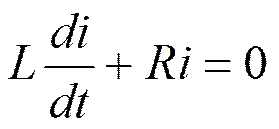
Мы знаем:

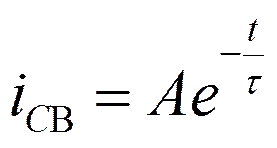, где

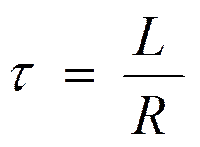
Частное решение:

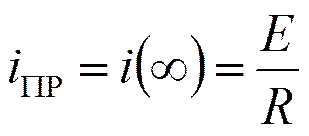
- принуждённая составляющая тока.

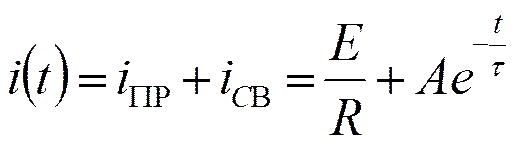
i(t)- полное решение.

Постоянную А найдём, используя ННУ.

 :       

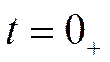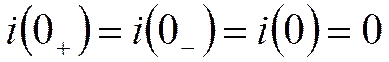
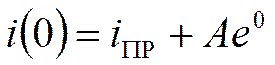
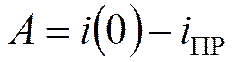
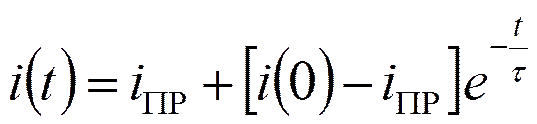
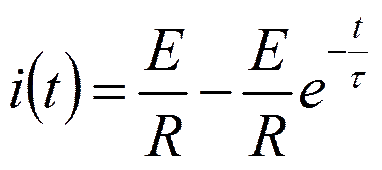
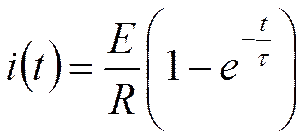
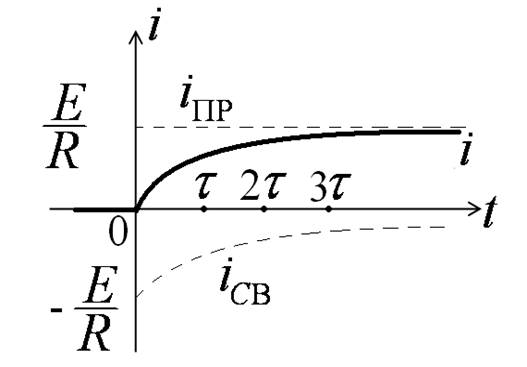
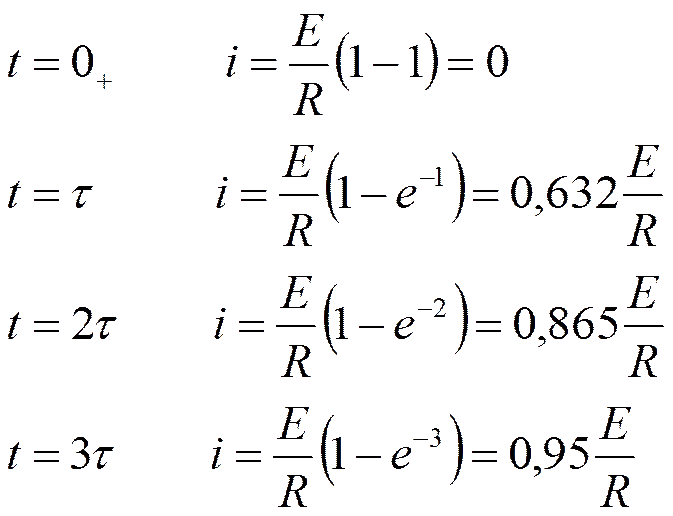
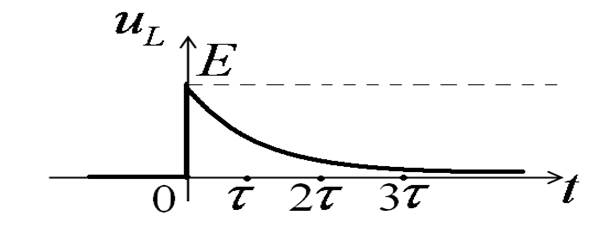
Принято считать, что переходный процесс заканчивается за время   t_пп » 3t.

Напряжение u_L(t):

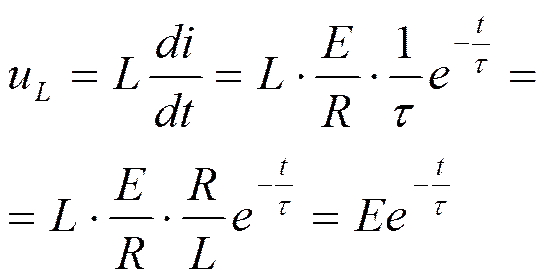
Включение цепи RL на синусоидальное напряжение

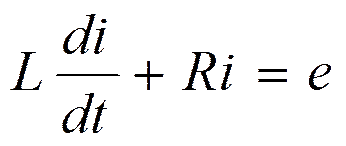
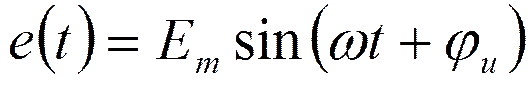
Решение однородного уравнения:

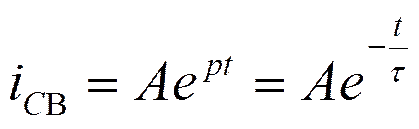
Частное решение:

;      

 :      

 

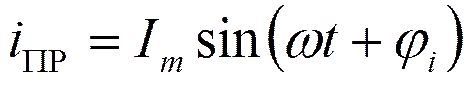
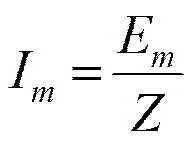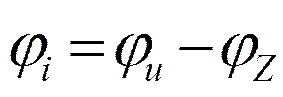
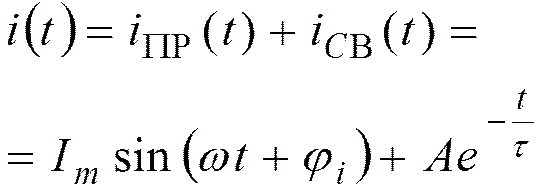
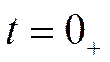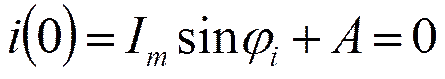
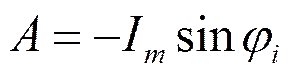
Переходный ток:

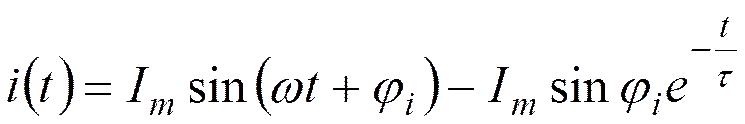
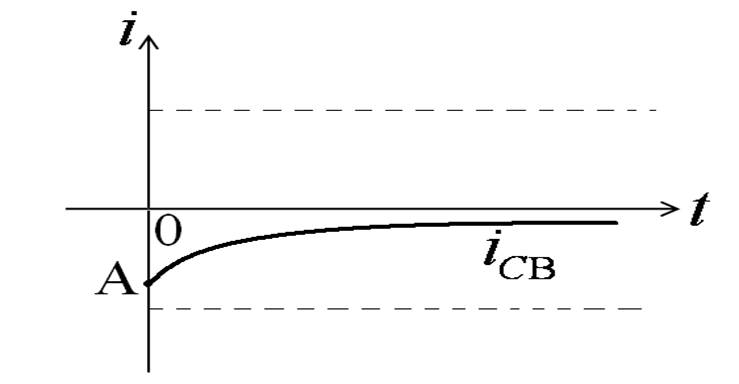
Переходный ток:

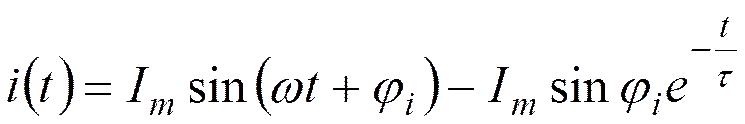
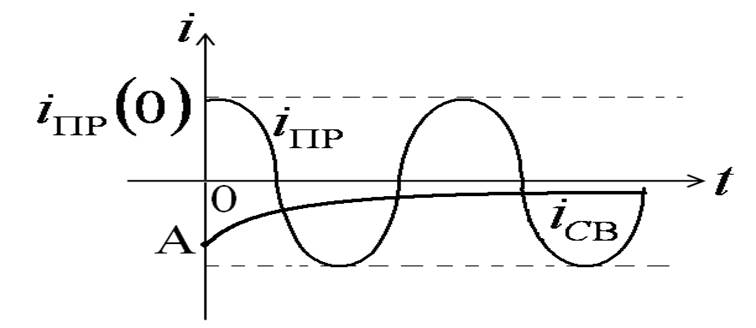
Переходный ток:

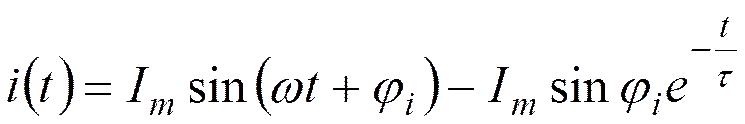
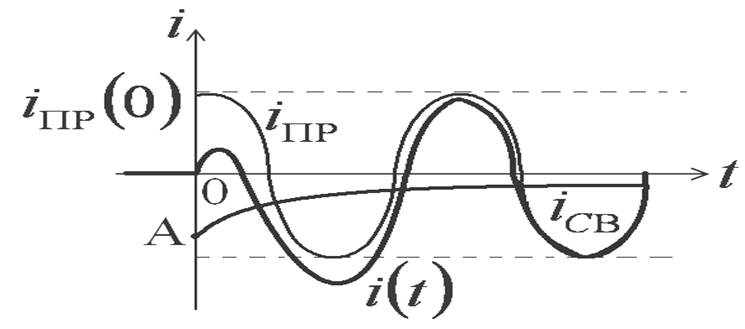
Короткое замыкание RC цепи

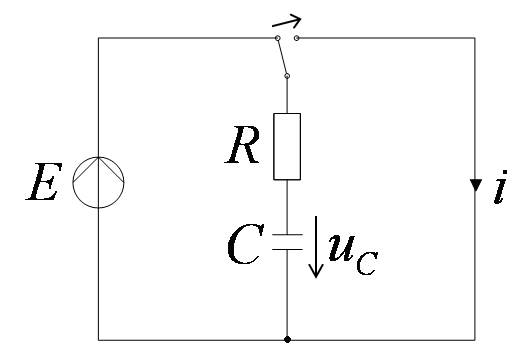
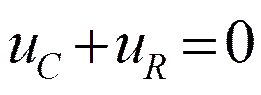          или

        

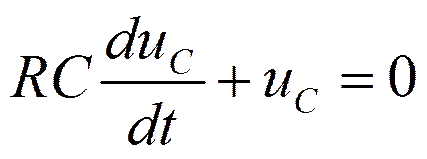
Откуда

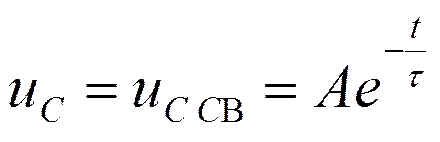, т.к.        u_{C пр}=0             

Свободная составляющая

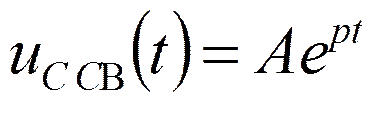, где р – корень характеристического уравнения

 ;      

 :       

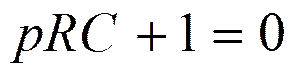
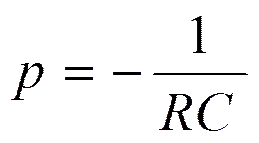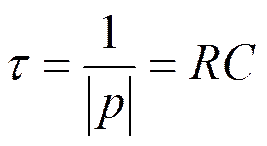
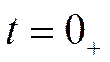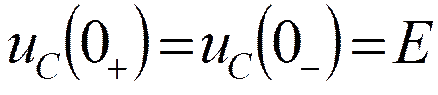
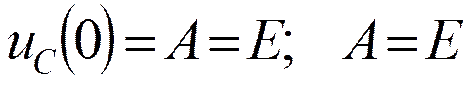
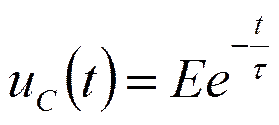
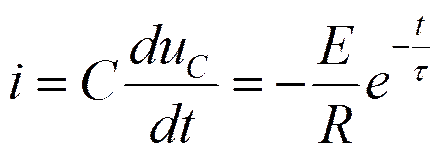
Включение цепи RC на постоянное напряжение

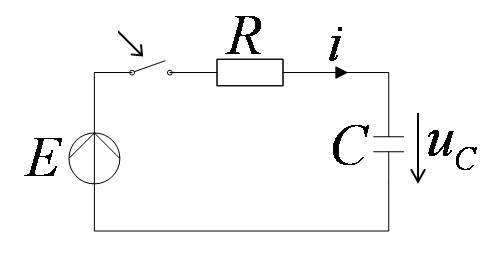
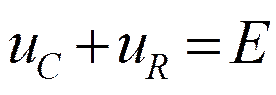
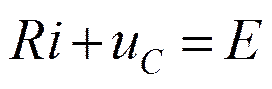
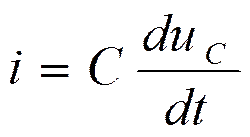
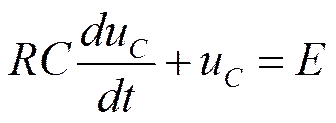
Свободная составляющая

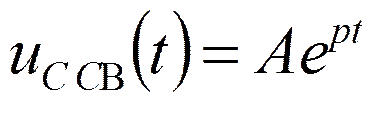, где р – корень характеристического уравнения

 ;      

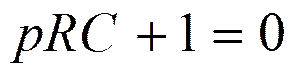
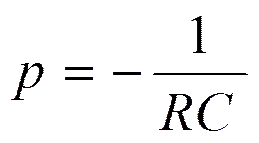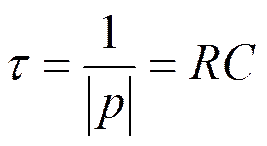
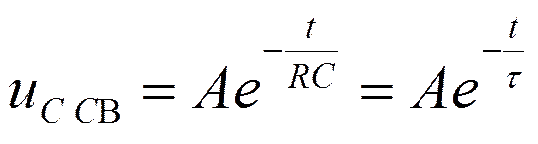
Принуждённая составляющая

 :       

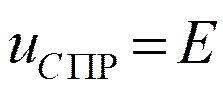
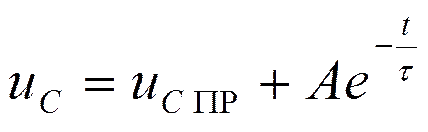
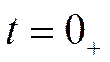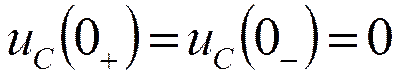
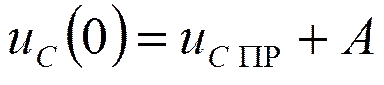
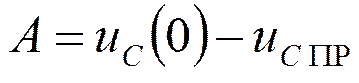
Откуда

 ;          

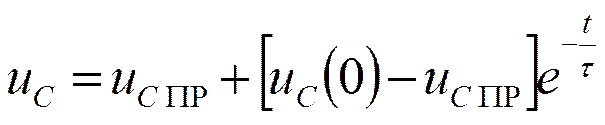
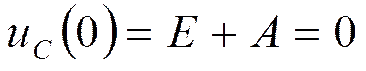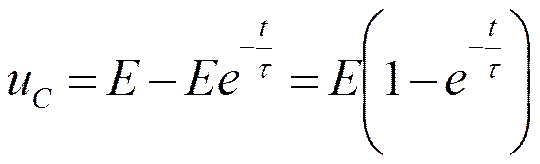
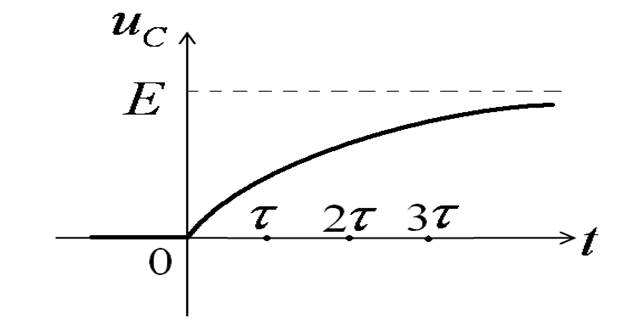
Ток в цепи

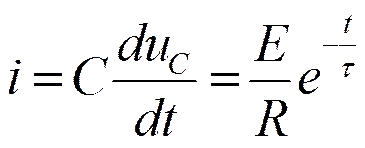
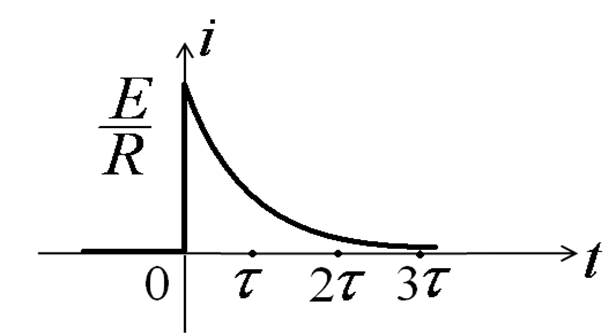
Включение RC цепи на синусоидальное напряжение

САМОСТОЯТЕЛЬНО!!!

Порядок расчёта сложных цепей с одним реактивным элементом

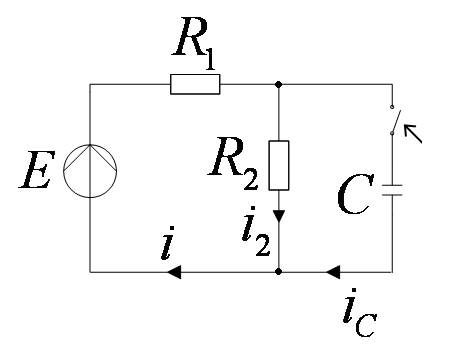
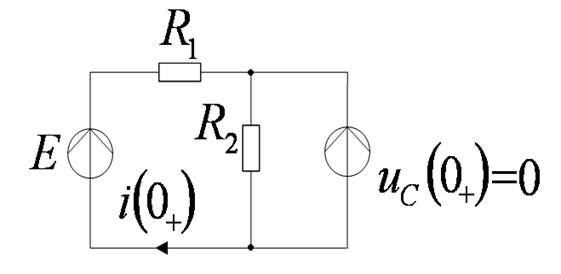
Найти ток i.

1.  По законам Кирхгофа составить интегро-дифференциальные уравнения

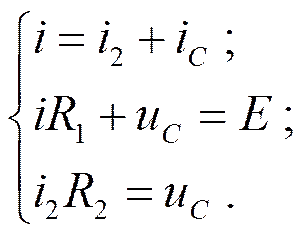
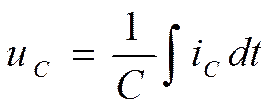
2.  Преобразовать их в дифференциальное уравнение 1-го порядка относительно тока i

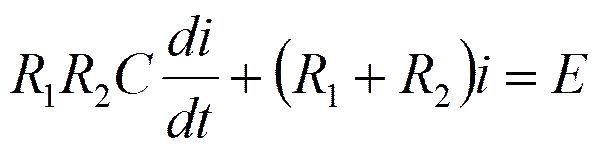
3.  Записать выражение для свободной составляющей

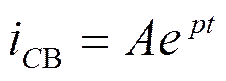  , где

 - корень уравнения

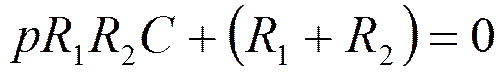
Откуда

;  

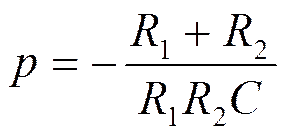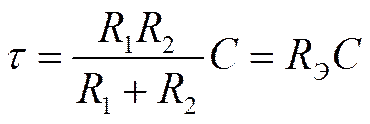
4.  Найти принуждённую составляющую

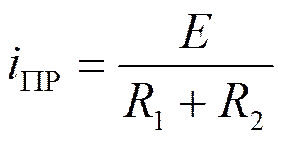
5.  Определить А.

 :       

;    

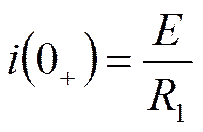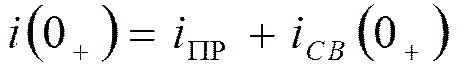     или

   ,

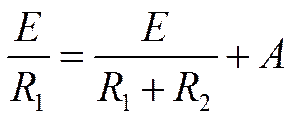Откуда

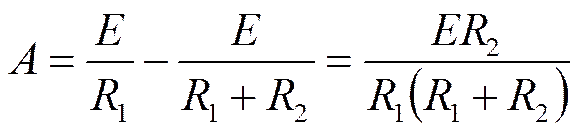
6.  Записать выражение для тока и построить график

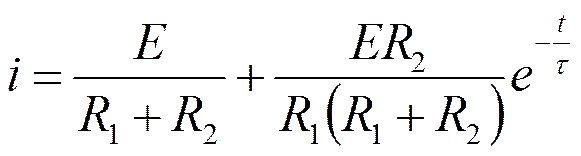
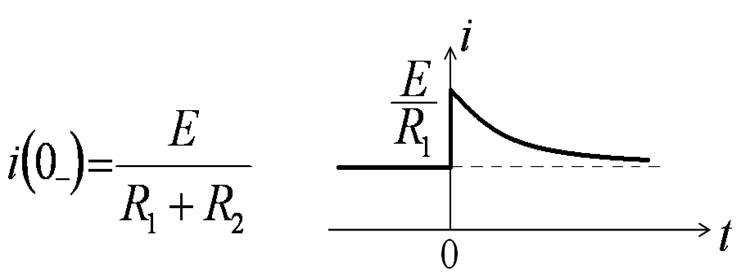
Внимание!!!

При расчёте этапы 1-3 можно опустить:

 Для цепей первого порядка можно сразу же записать решение в виде

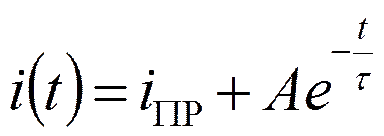
или

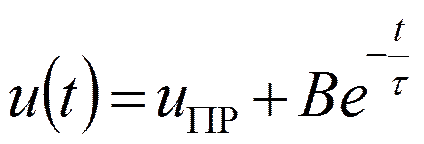
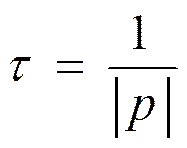
Корень характеристического уравнения можно найти, не составляя уравнения рассмотренным ранее способом

Достаточно найти сопротивление Z цепи,разорвав

её в любом месте, где протекает ток, и заменив 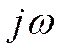 на p.

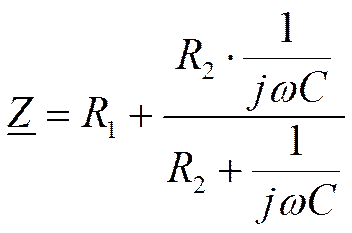
Заменим

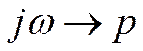
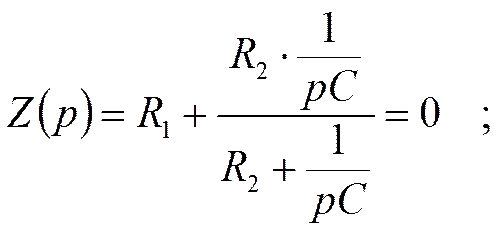
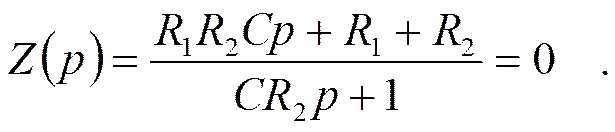
Откуда:

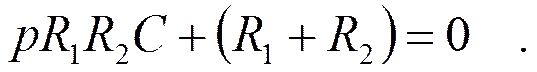
Для цепей первого порядка постоянная времени  равна:

· для  RL цепи

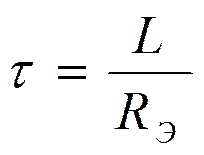
· для RC цепи

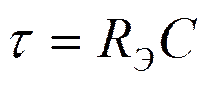
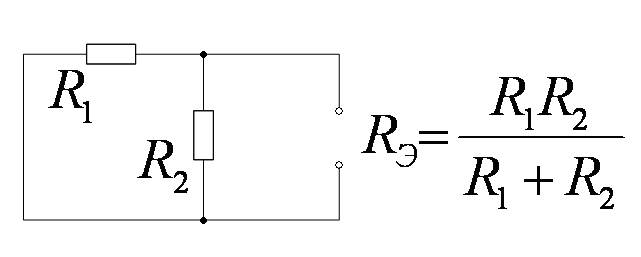
где R_э - внутреннее сопротивление эквивалентного генератора, образованного цепью относительно реактивного элемента.