2.6 Метод наложения
применяют для линейной цепи, содержащей несколько источников
Принцип наложения
Реакция линейной электрической цепи на сумму воздействий равна сумме реакций от каждого воздействия
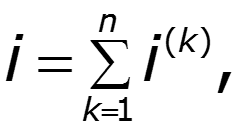
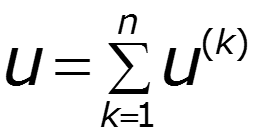
- число источников
![]()
Алгоритм расчета
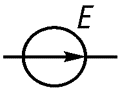
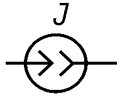
а) составить комплект частичных схем, число которых равно числу источников. В каждой из схем оставить один источник, остальные заменить их внутренними сопротивлениями.
![]()
![]()
![]()
![]()
![]()
![]()
4. Определить токи в исходной схеме как алгебраическую сумму частичных токов.
Пример
![]()
![]()
![]()
![]()
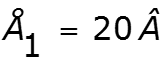
![]()
![]()
Частичная схема 1
![]()
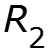
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
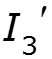
![]()
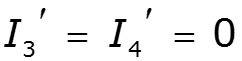
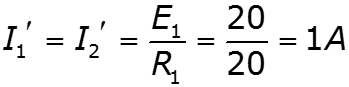
Частичная схема 2
![]()
![]()
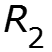
![]()
![]()
![]()
![]()
![]()
![]()
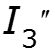
![]()
![]()
![]()
![]()
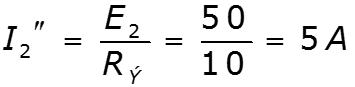
![]()
![]()
![]()
![]()
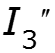
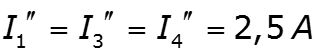
Частичная схема 3
![]()
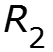
![]()
![]()
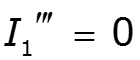
![]()
![]()
![]()
![]()
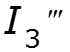
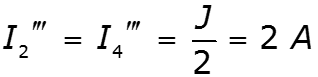
![]()
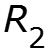
![]()
![]()
![]()
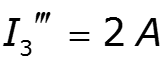
![]()
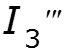
Найдем результирующие токи
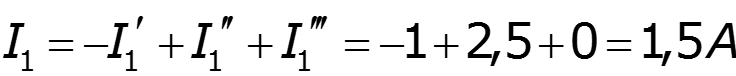
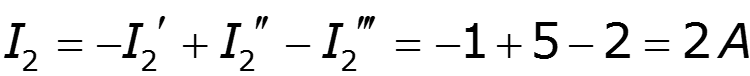
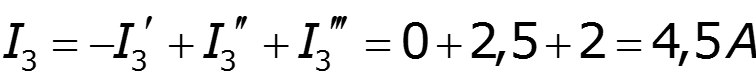
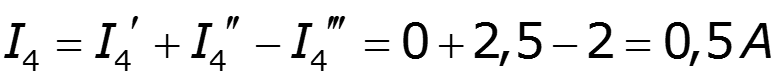
2.7 Баланс мощности выражает закон сохранения энергии в электрической цепи и позволяет проверить правильность произведенных расчетов.
Сумма мощностей, отдаваемых независимыми источниками, равна сумме мощностей, потребляемых остальными элементами электрической цепи.
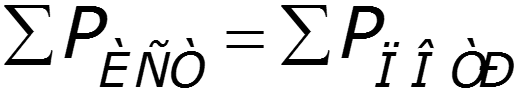
Алгоритм расчета
1.Рассчитать схему любым методом. 2.Определить мощность каждого из источников: а) , если направления и совпадают
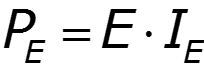
![]()
![]()
![]()
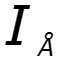
б) , если и направлены противоположно в) Напряжение на источнике определяют, используя второй закон Кирхгофа.
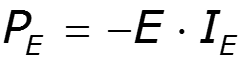
![]()
![]()
![]()
![]()
![]()
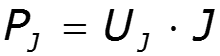
![]()
![]()
3. Определить мощность, потребляемую каждым из резисторов. 4.Проверить баланс. Погрешность при расчете баланса не должна превышать 5%
![]()
![]()
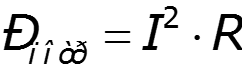
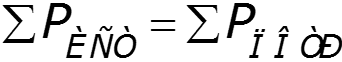
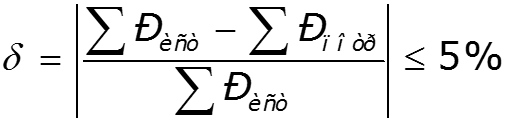
Пример
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
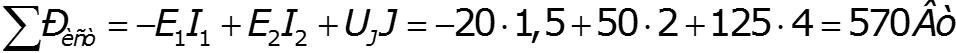
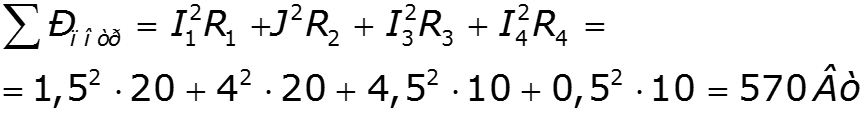
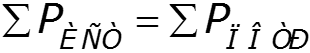
Пример
![]()
![]()
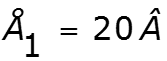
![]()
![]()
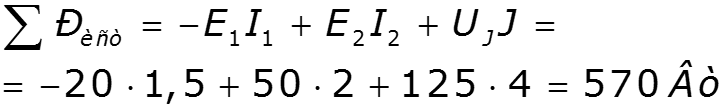
2.8 Расчет электрических цепей методом законов Кирхгофа.
Метод без преобразования схемы
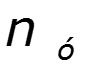
- число узлов - число ветвей - число источников тока
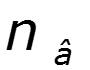
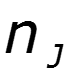
Алгоритм расчета
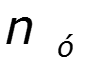
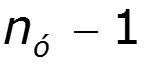
4. Выбрать направление обхода независимых контуров. (Независимый контур – контур, содержащий хотя бы одну ветвь, не входящую в другие контуры). Контур не должен содержать ветвь с источником тока. 5. Составить уравнения по ЗНК. Число уравнений 6. Решить систему уравнений. (Число уравнений системы равно числу неизвестных).
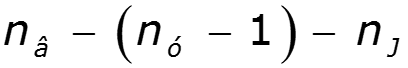
Пример
2
1
![]()
![]()
I
II
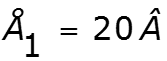
![]()
![]()
3
![]()
1
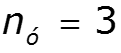
![]()
2
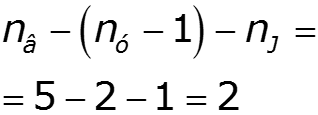
![]()
I
![]()
II
2.9 Метод контурных токов
Метод без преобразования схемы
Основная задача – уменьшить число независимых уравнений Определение контурных токов – на основании уравнений по ЗНК Определение токов в ветвях – на основании уравнений по ЗТК Метод удобен для схем с большим числом узлов и малым числом независимых контуров.
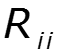
- собственное сопротивление контура – сумма сопротивлений ветвей, входящих в данный контур - взаимное сопротивление контуров и - сумма сопротивлений ветвей, входящих одновременно в оба контура - собственная ЭДС контура - алгебраическая сумма ЭДС, действующих в данном контуре
![]()
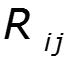
![]()
![]()
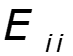
![]()
Алгоритм расчета
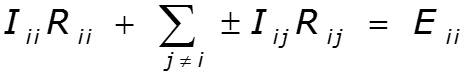
Пример
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
I
II
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
III
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Особенности метода для схем, содержащих источник тока
Пример
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
I
![]()
II
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
III
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2. 10 Метод узловых потенциалов
Метод без преобразования схемы
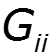
- собственная проводимость узла - сумма проводимостей ветвей, подходящих к данному узлу - взаимная проводимость узлов и - сумма проводимостей ветвей, соединяющих узлы и - узловой ток – алгебраическая сумма источников тока, подключенных к узлу базисный узел –узел, значение потенциала которого принимается равным нулю.
![]()
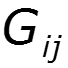
![]()
![]()
![]()
![]()
![]()
![]()
Алгоритм расчета
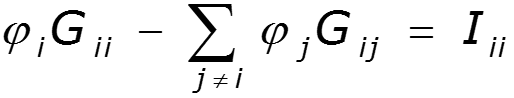
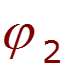
Пример
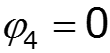
![]()
![]()
![]()
![]()
![]()
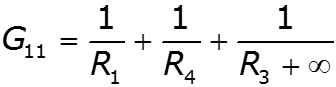
![]()
![]()
![]()
![]()
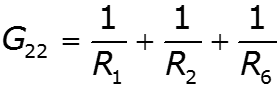
![]()
![]()
![]()
![]()
![]()
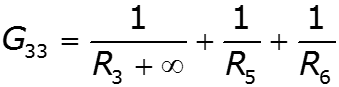
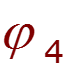
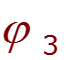
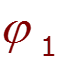
![]()
![]()
![]()
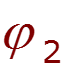
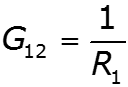
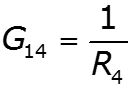
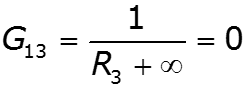
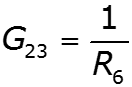
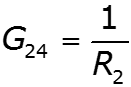
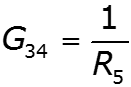
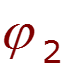
![]()
![]()
![]()
![]()
![]()
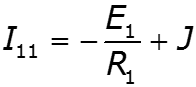
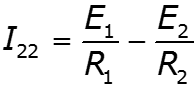
![]()
![]()
![]()
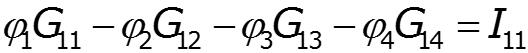
![]()
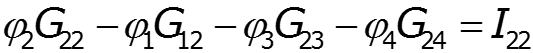
![]()
![]()
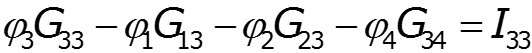
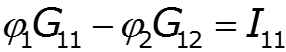
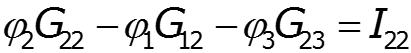
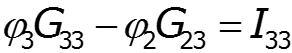
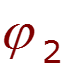
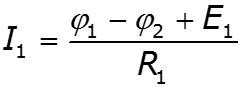
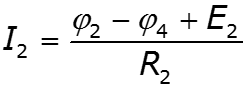
![]()
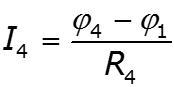
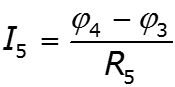
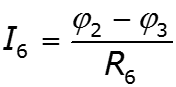
Особенности метода для схем, содержащих идеальный источник ЭДС
![]()
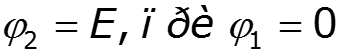
![]()
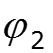
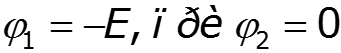
Пример
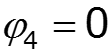
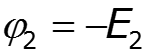
![]()
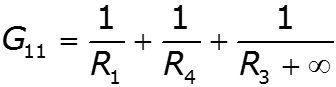
![]()
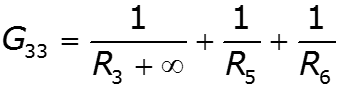
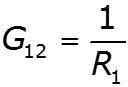
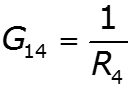
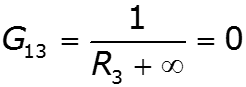
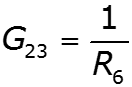
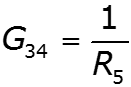
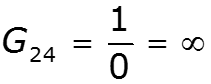
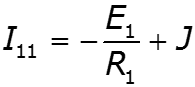
![]()
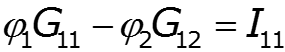
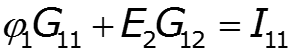
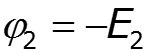
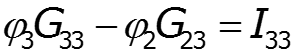
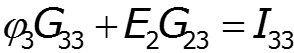
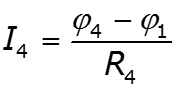
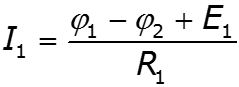
![]()
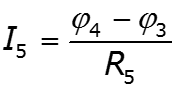
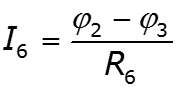
![]()
Метод двух узлов
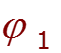
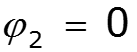
![]()
![]()
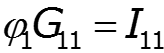
![]()
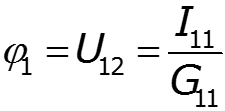
![]()
![]()
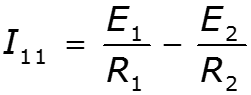
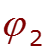
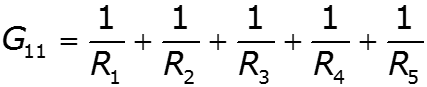
2.11 Метод эквивалентного генератора
Теорема об активном источнике напряжения (Тевенина)
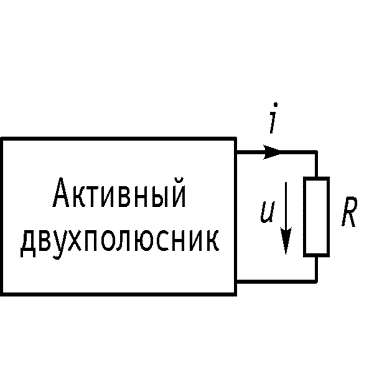
Ток в любой ветви линейной электрической цепи не изменится, если активный двухполюсник, к которому подключена данная ветвь, заменить эквивалентным источником напряжения, с задающим напряжением, равным напряжению холостого хода на зажимах исходной цепи, и внутренним сопротивлением, равным эквивалентному входному сопротивлению пассивного двухполюсника со стороны разомкнутой ветви.
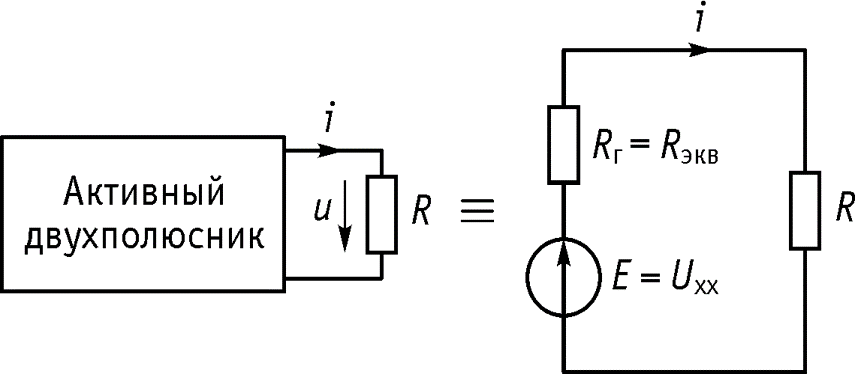
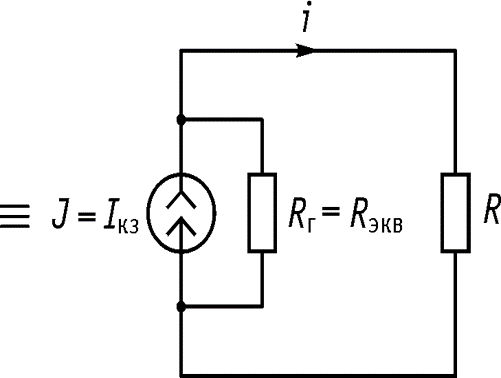
Теорема об активном источнике тока (Нортона)
Ток в любой ветви линейной электрической цепи не изменяется, если активный двухполюсник, к которому подключена данная ветвь, заменить эквивалентным источником тока с задающим током, равным току короткого замыкания этой ветви, и внутренней проводимостью, равной эквивалентной входной проводимости со стороны разомкнутой ветви.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.