Треугольники сопротивлений, напряжений, мощностей.
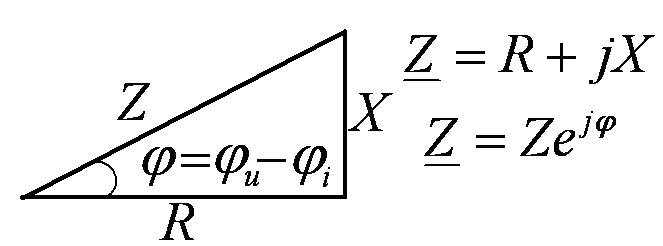
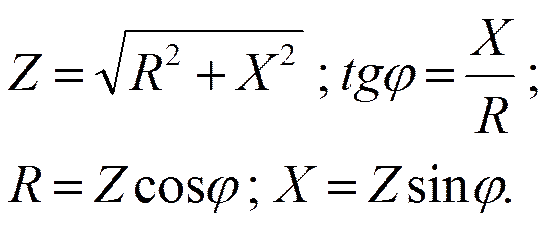
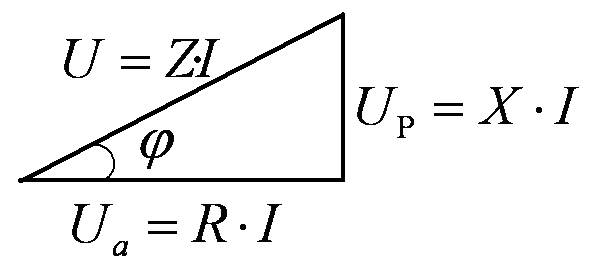
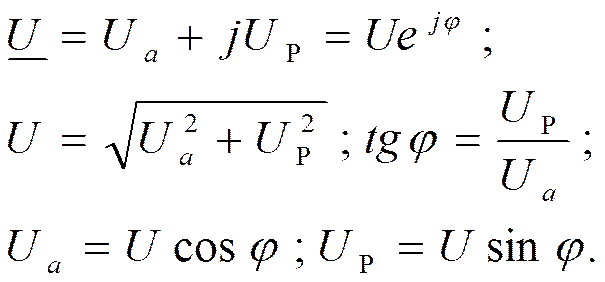
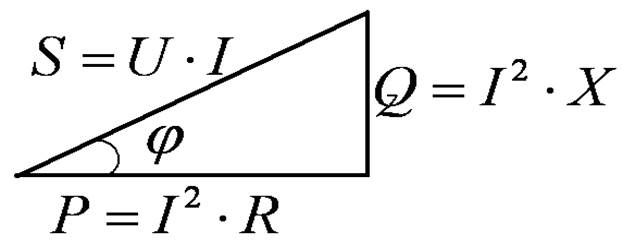
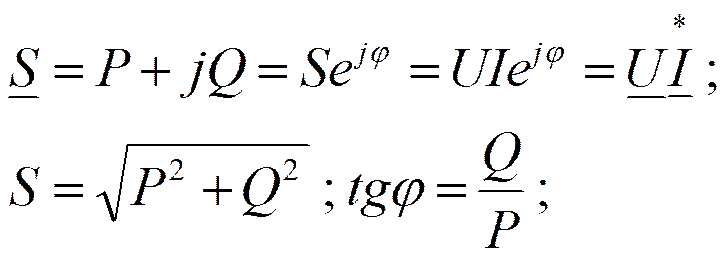
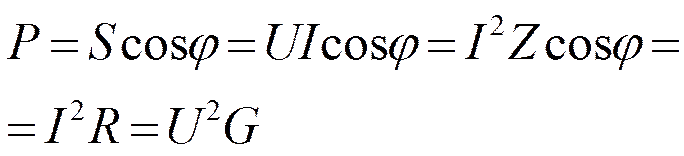
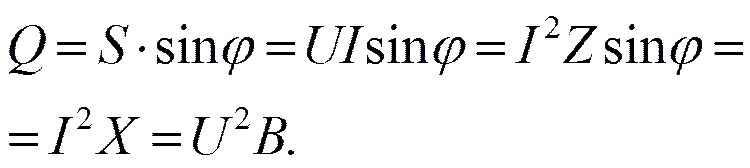

2.3. Законы Ома и Кирхгофа в комплексной форме
 |
Закон Ома

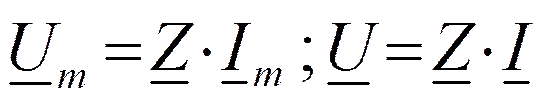
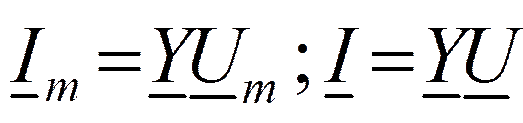
Законы Кирхгофа

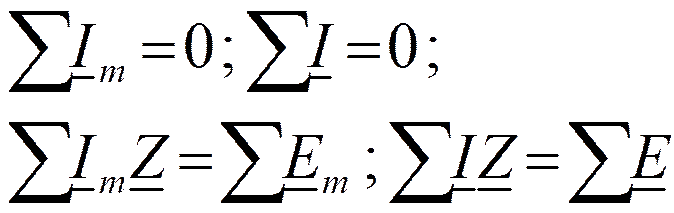

2.4. Расчёт цепей символическим методом
 |
Расчёт цепи состоит в определении токов в ветвях и напряжений на элементах схемы.
Расчёт цепи с одним источником
![]()
![]()
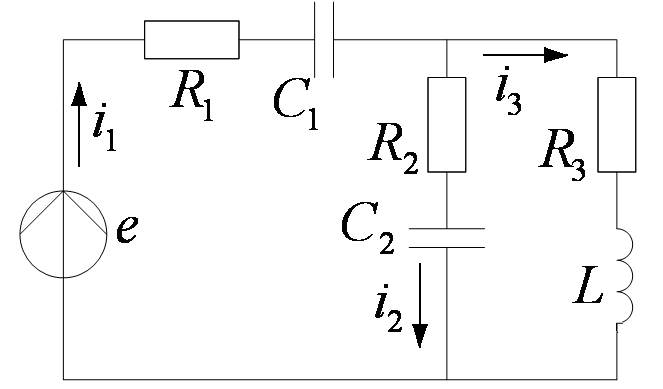
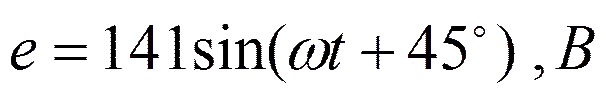
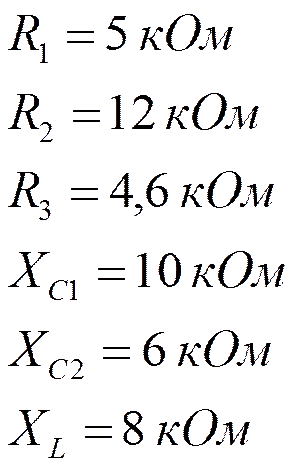
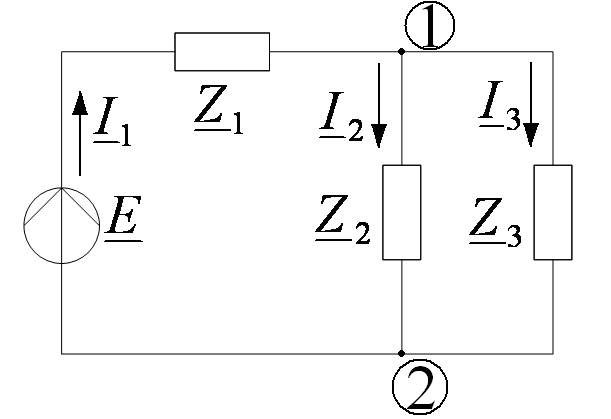
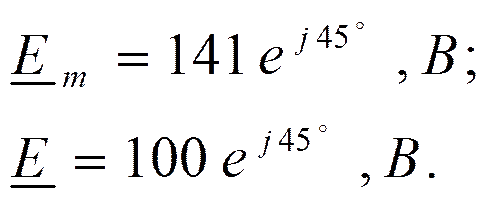
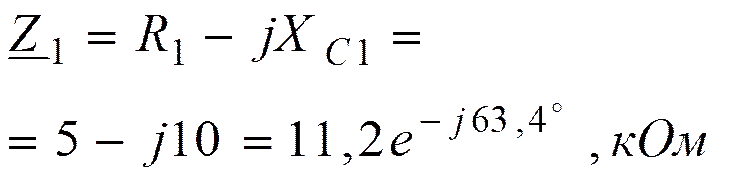
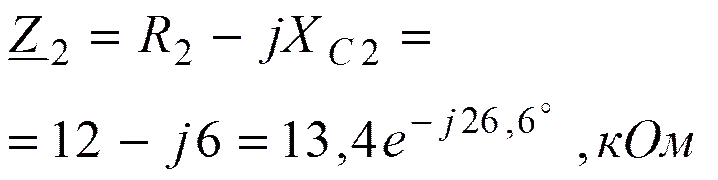
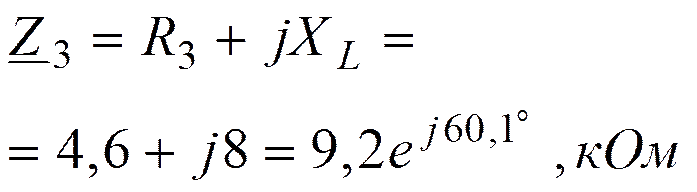
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
||
Это расчётные формулы, основанные на законах Ома и Кирхгофа.
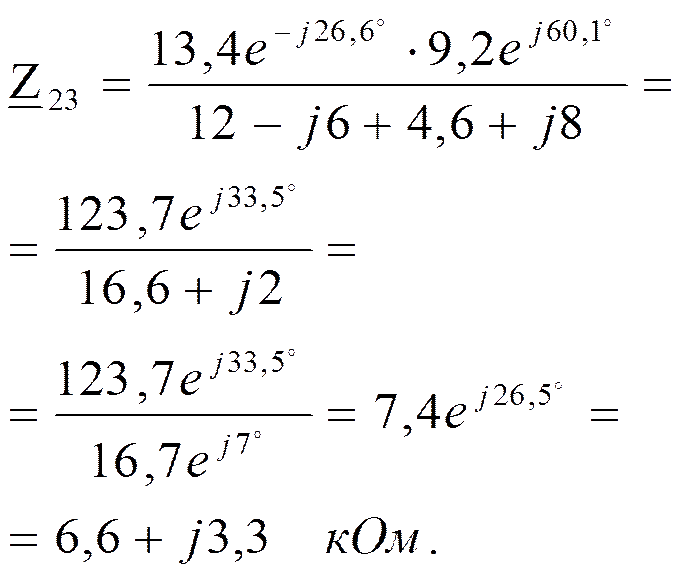
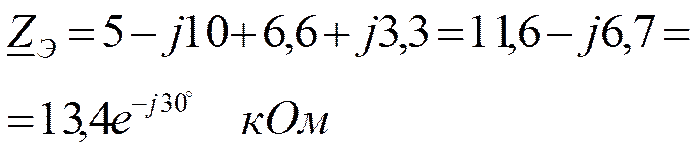
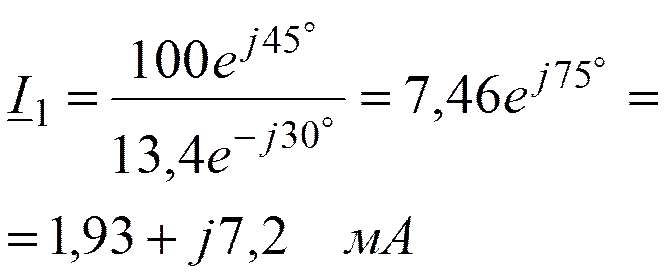
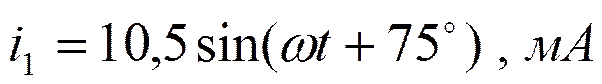
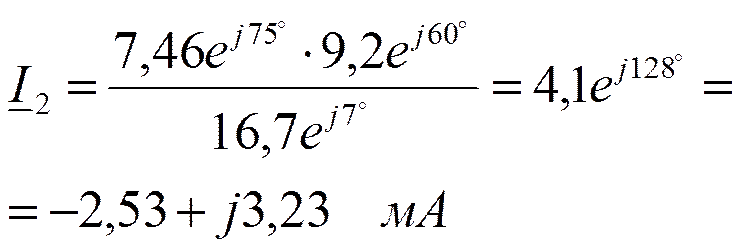
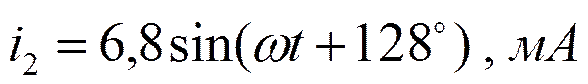
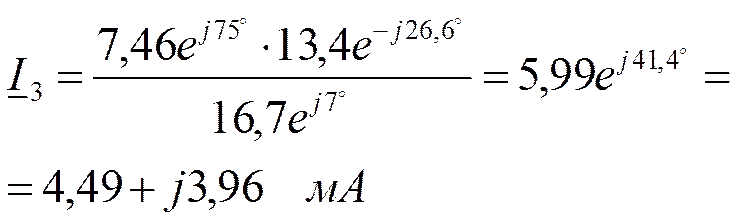
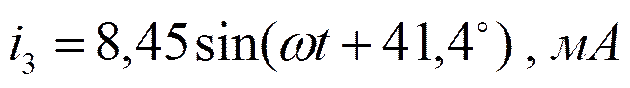
Построим векторные диаграммы токов.
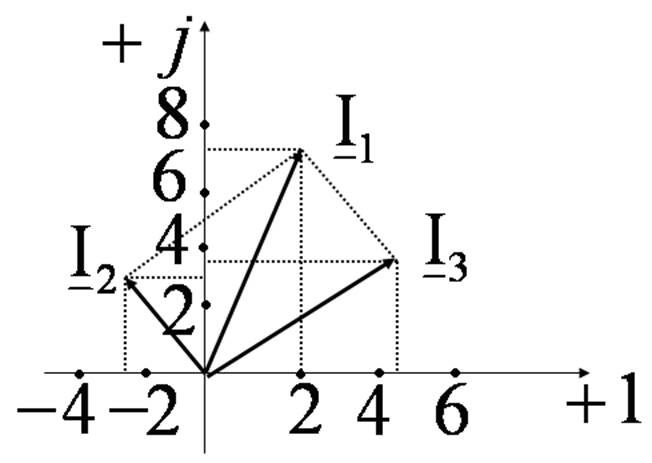
Расчёт цепи с несколькими источниками
а) Метод наложения.
б) Метод законов Кирхгофа.
в) Метод узловых напряжений (потенциалов).
г) Метод контурных токов.
а) Метод наложения.
Порядок расчёта:
1. Выбрать и указать на исходной схеме направление токов ветвей.
2. Составить частичные схемы. В каждой схеме оставить только один источник, остальные заменить их внутренним сопротивлением (ЭДС - короткое замыкание, источник тока – разрыв).
3. Рассчитать частичные токи в ветвях каждой из схем.
4. Ток в любой ветви исходной схемы определяется как алгебраическая сумма соответствующих частичных токов.
Пример:
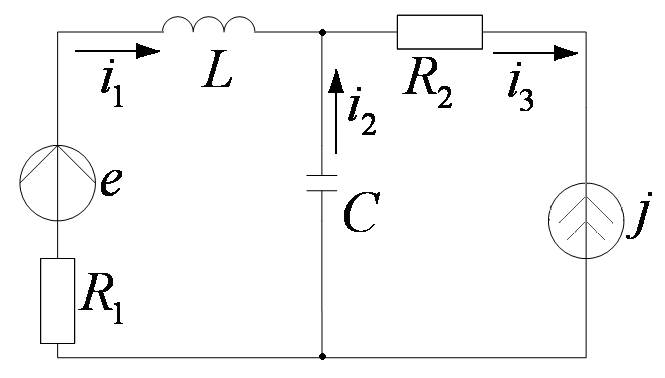
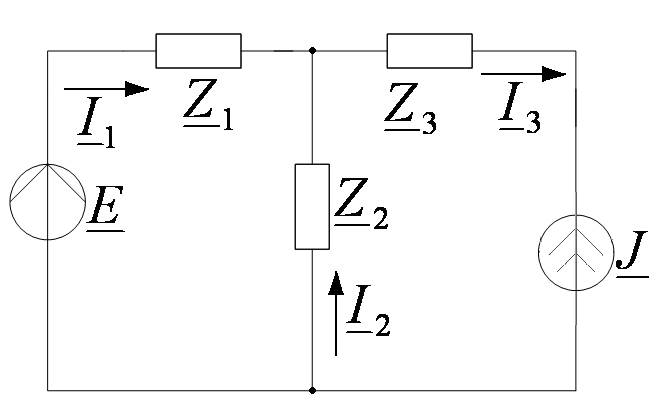
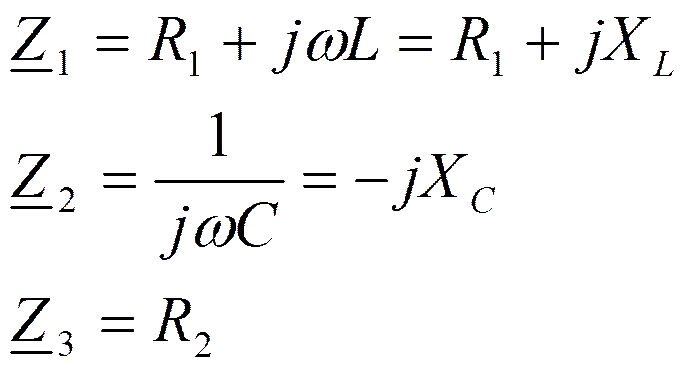
Первая частичная схема:
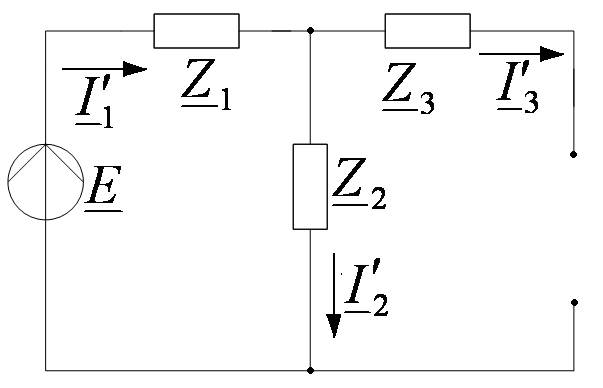
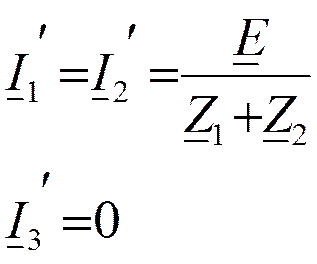
Вторая частичная схема:
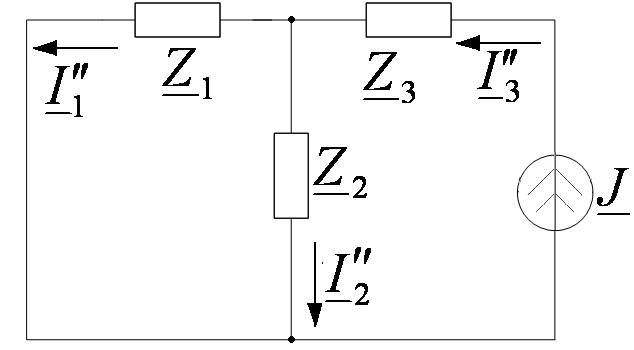
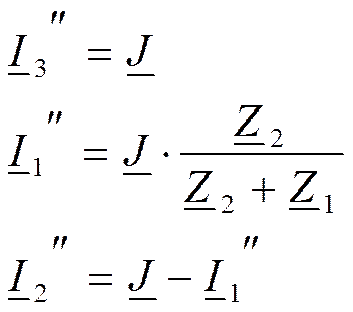
Токи в ветвях:
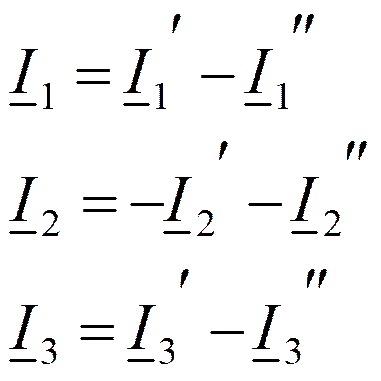
б) Метод законов Кирхгофа.
САМОСТОЯТЕЛЬНО
в) Метод узловых напряжений
- Выбрать произвольно направления токов в ветвях.
- Пронумеровать узлы.
- Заземлить один из узлов.
- Составить уравнения состояния.
- Найти из системы потенциалы узлов.
- Вычислить токи в ветвях.
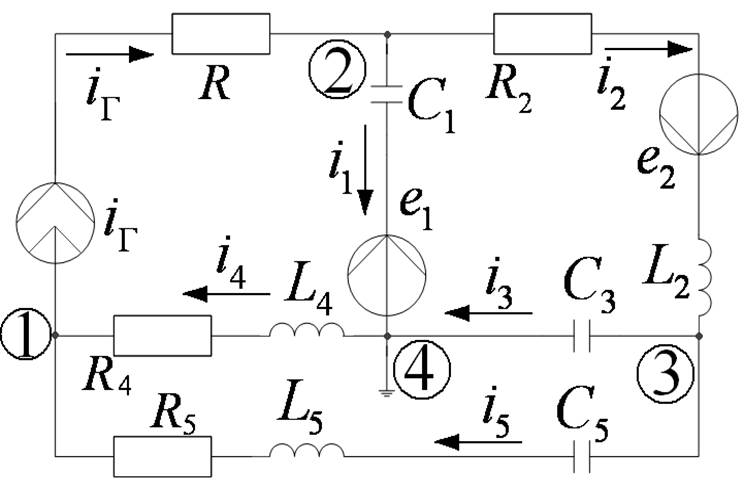
Токи в ветвях:
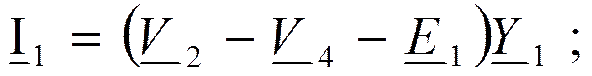
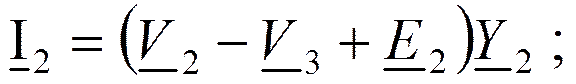

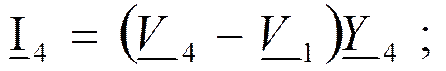
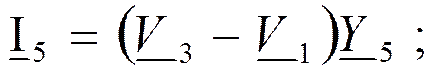
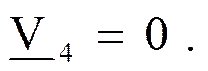
Проводимости ветвей:
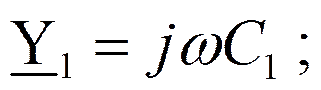

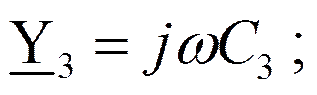
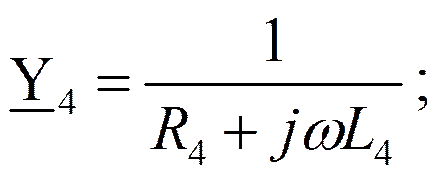
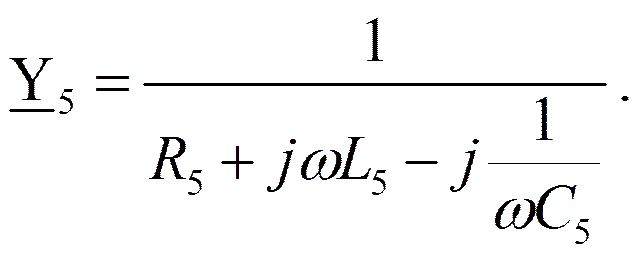
Собственные проводимости узлов:
Узел 1
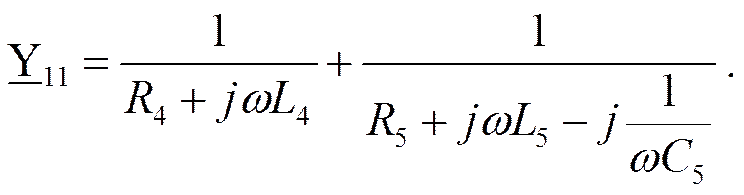
|

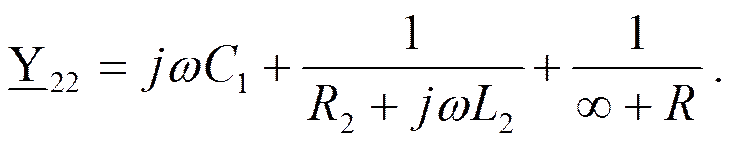
Узел 3
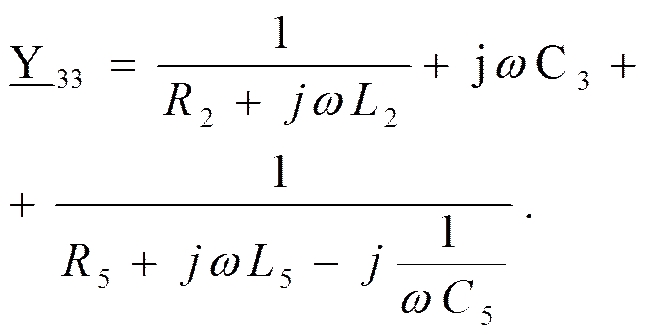
Взаимные проводимости узлов:
Узлы 1 и 2
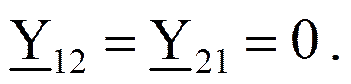
Узлы 2 и 3
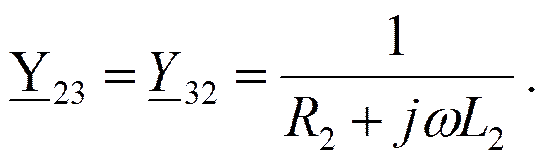
Узлы 1 и 3
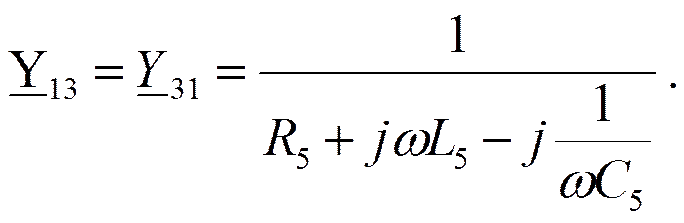
Система уравнений:
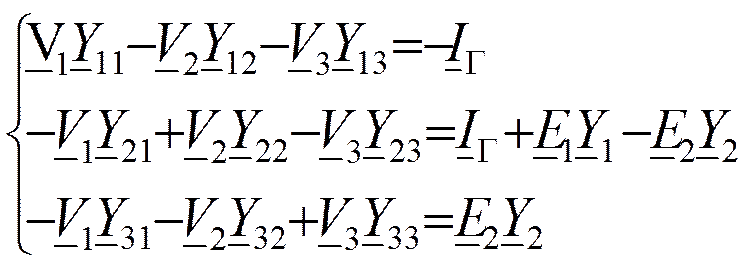
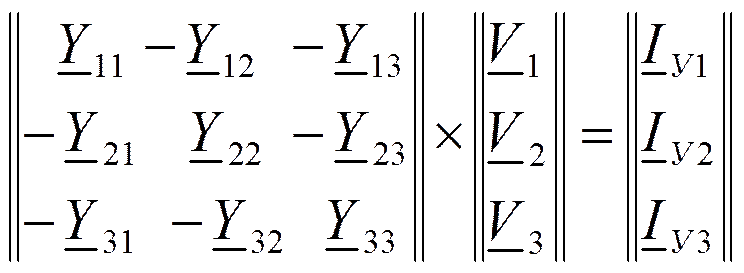
Iу - узловой ток, равный алгебраической сумме токов генераторов, втекающихв данный узел или вытекающих из него.
 |
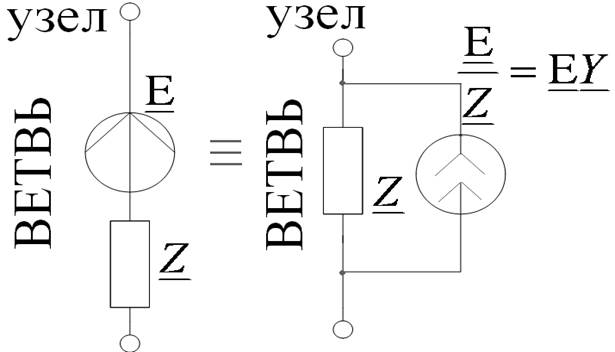
Правило знаков:
![]()
Собственные проводимости входят в уравнения со знаком «+», а взаимные проводимости – со знаком «-».
![]()
Узловые токи (т.е. токи генераторов) входят в правые части уравнений со знаком «+», если они втекают в узел, и со знаком «-», если вытекают из узла.
![]()
Особенность расчета МУН
Если в схеме есть ветвь, содержащая идеальный источник напряжения, то заземлять нужно один из узлов, к которому подключен этот источник. Тогда потенциал другого узла равен +Е или –Е.
|
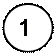
 если
если
![]()
![]()
![]()
![]()
![]()
 V1=0, то
V1=0, то
V2=E
|

![]()
 V2=0, то
V2=0, то
![]()
![]()
![]() V1=-E
V1=-E
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.