III Электрические цепи при синусоидальном (гармоническом) воздействии
3.1 Гармонические колебания. Основные понятия и определения.
Гармоническое колебание – движение или изменение состояния материальных тел или материи (W, q, I, U, P) вокруг некоторого среднего значения по закону простейшей периодической функции вида .
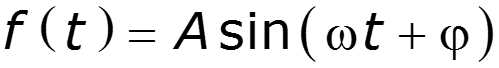

![]()
![]()
![]()
![]()
![]()
Амплитуда – максимальное отклонение от среднего значения
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
Начальная фаза [градус], [рад] – значение смещения синусоиды относительно начала координат до точки перехода синусоиды из отрицательной полуволны в положительную

![]()
![]()
![]()
![]()
![]()
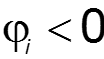
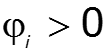

![]()
![]()
![]()
![]()
![]()
![]()
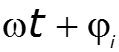
Текущая фаза (рад)– функция времени, значение которой отсчитывается от начала координат t = 0 до некоторого текущего значения

![]()
![]()
![]()
![]()
![]()
;
![]()
![]()
.
Период - время, за которое совершается одно полное колебание - частота колебаний
![]()
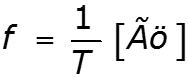

![]()
![]()
![]()
![]()
![]()
![]()
![]()
Угловая частота [рад/c]– скорость изменения текущей фазы
![]()
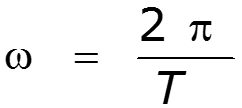
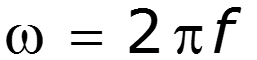

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Мгновенное значение - значение функции в произвольный момент времени
![]()

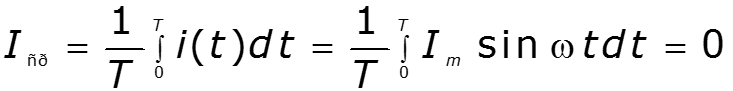
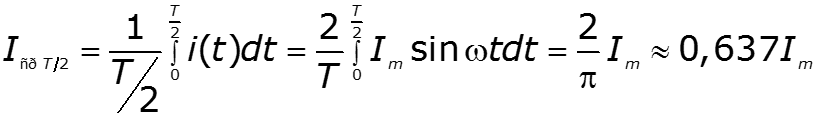
.
Действующее значение за период
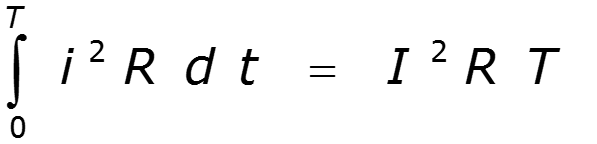
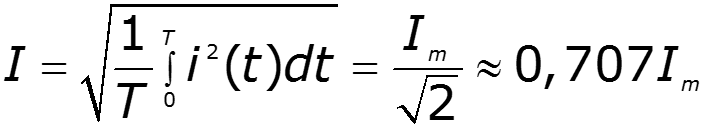
![]()
3.2 Способы представления гармонических колебаний
I форма записи - гармоническое колебание как функция времени
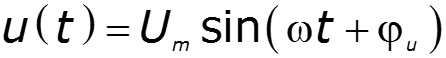

Законы Кирхгофа для мгновенных значений
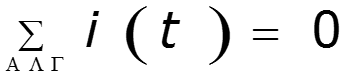
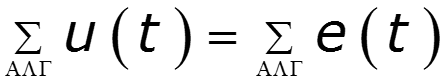
Пример
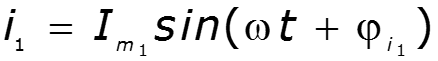
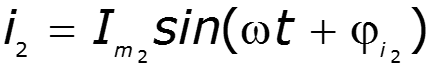
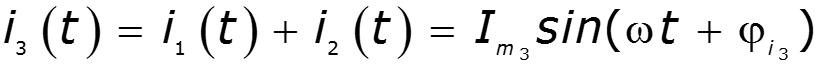
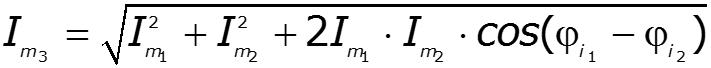
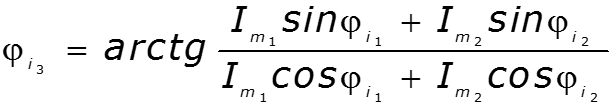
II форма записи – векторная (классическая)
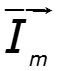
![]()
![]()
![]()
- проекция вектора на ось ординат
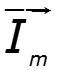
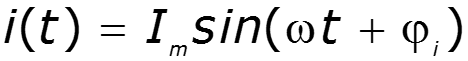
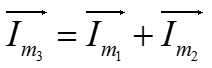
Законы Кирхгофа в векторной форме
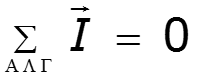
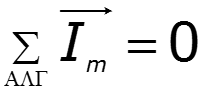
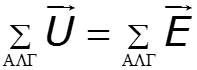
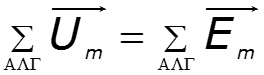
Расчет классическим методом сопровождается построением векторных диаграмм
III форма записи -символическая
Информация о гармоническом колебании заключена в длине вектора и его начальной фазе
Действия над векторами можно заменить действиями над комплексными числами
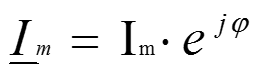
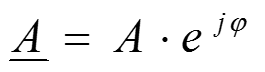
Переход от одной формы к другой
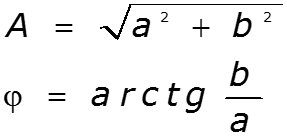
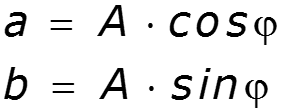
![]()
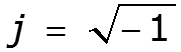
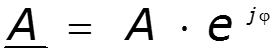
Действия над комплексными числами
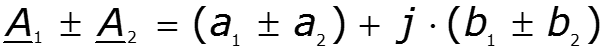
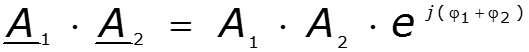
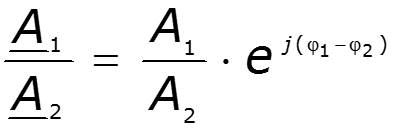
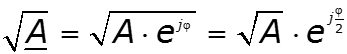
![]()
![]()
![]()
![]()
![]()
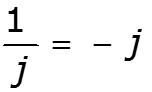
![]()
![]()
![]()
![]()
![]()
![]()
Комплексно-сопряженные числа
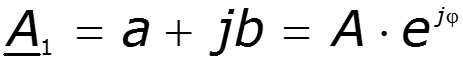
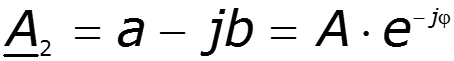
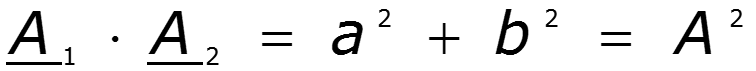
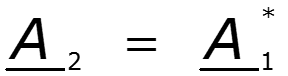
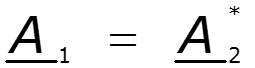
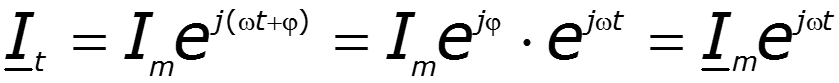
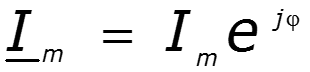
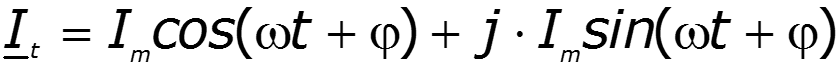
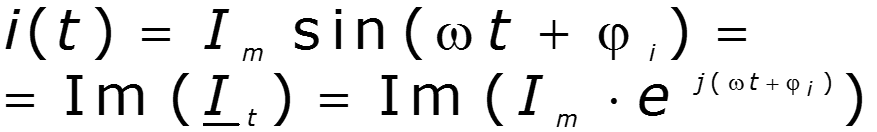
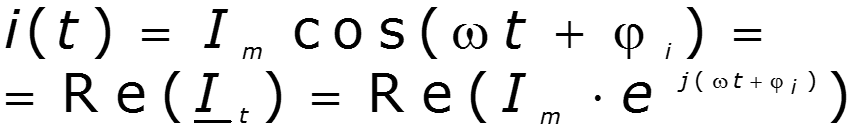
Законы Кирхгофа в комплексной форме
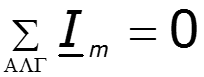
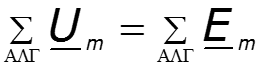
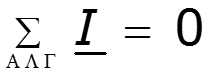
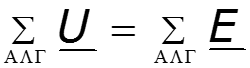
Пример
![]()
![]()
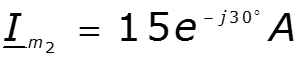
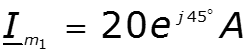
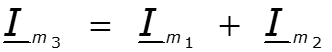

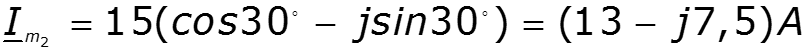
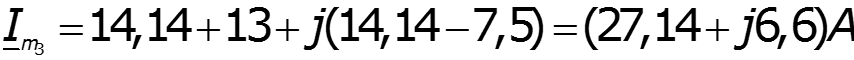
Пример
![]()
![]()
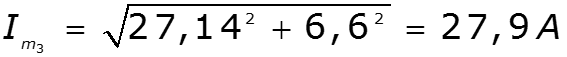
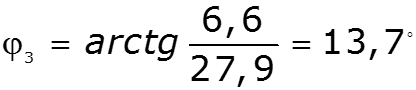
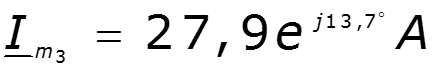
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.