
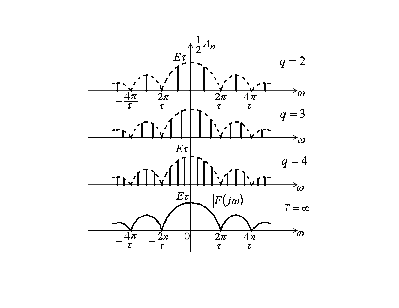


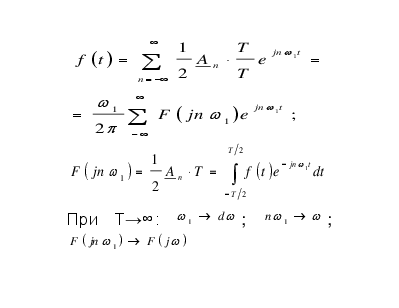





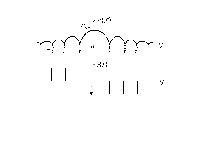




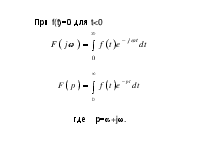

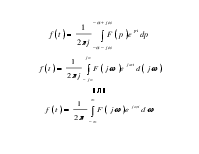


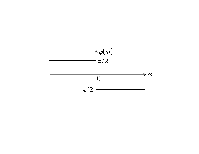
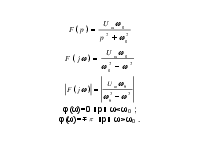

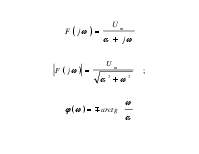

10.3. Спектры непериодических сигналов
 |
Отложим по оси ординат величину
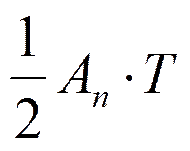
Обозначим
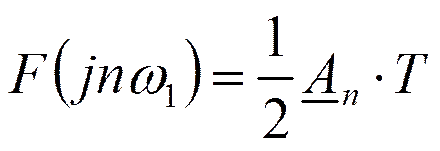
Ряд Фурье в комплексной форме
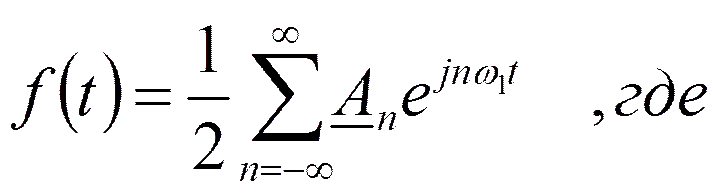
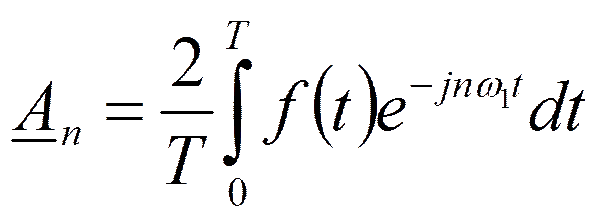
Устремим Т→∞ и совершим предельный переход.
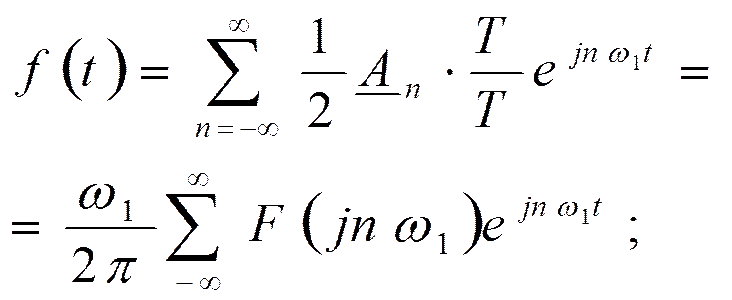
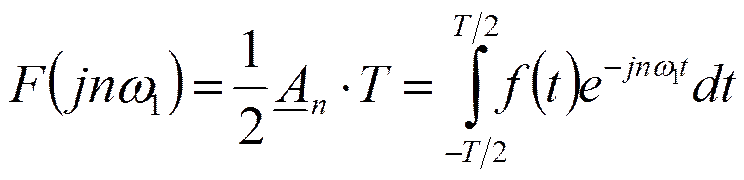 При Т→∞:
При Т→∞: 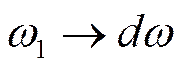 ;
;  ;
; 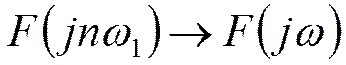

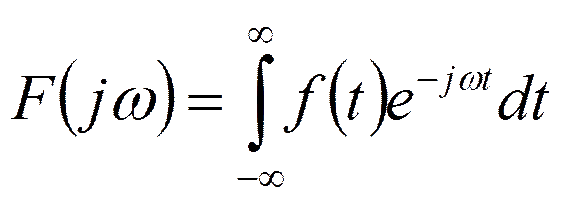
- прямое преобразование Фурье

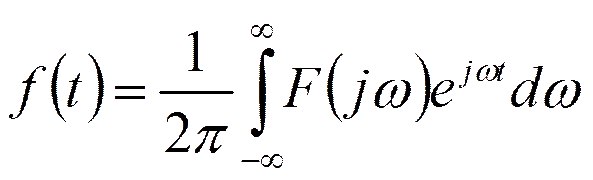
- обратное преобразование Фурье (интеграл Фурье)
F(jω)-комплексная спектральная плотность
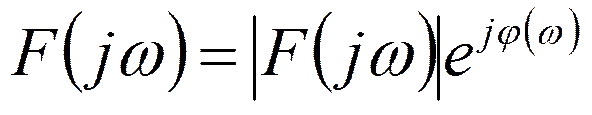
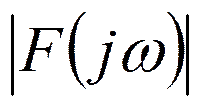 -спектральная
плотность амплитуд
-спектральная
плотность амплитуд
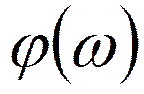 - спектральная
- спектральная
плотность фаз
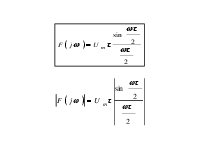
Спектр прямоугольного импульса
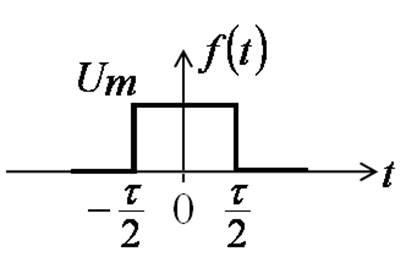
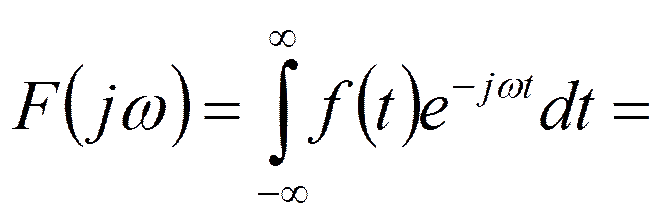
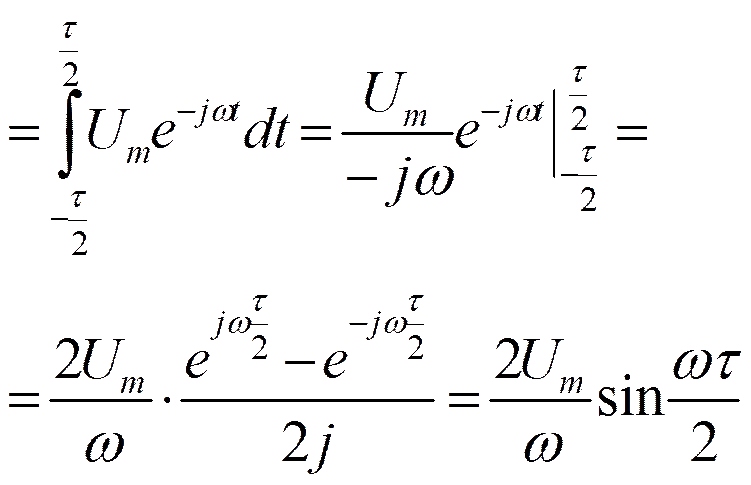

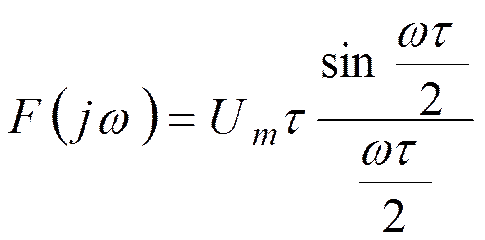
![]()
![]()
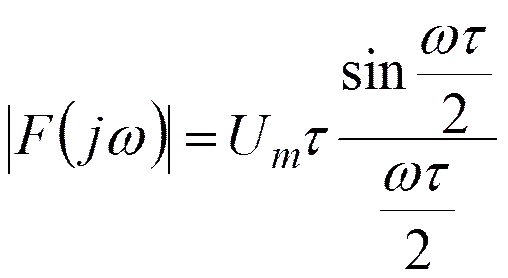
При ω=0
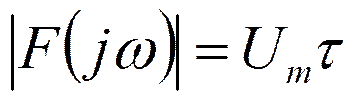
Нули спектральной плотности амплитуд:
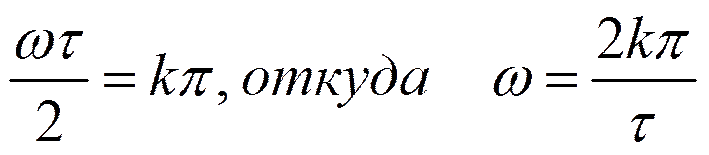
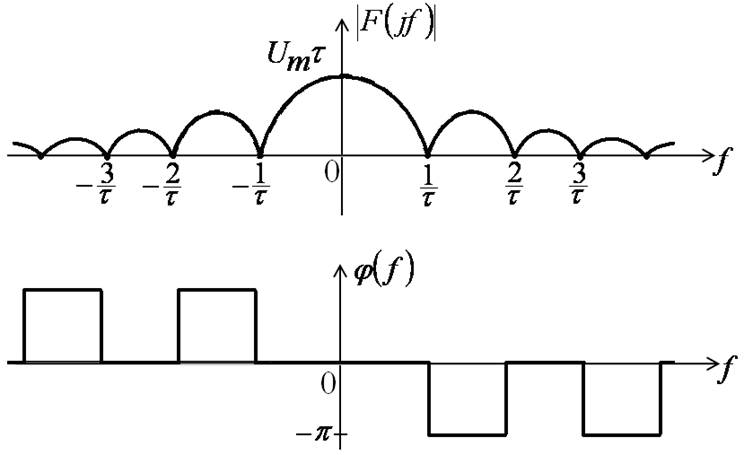
В пределах первого лепестка спектра сосредоточено около 90% всей энергии импульса.
За ширину спектра импульса можно принять полосу частот
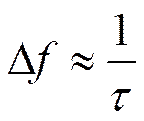
![]()
Чем короче импульс, тем шире его спектр.
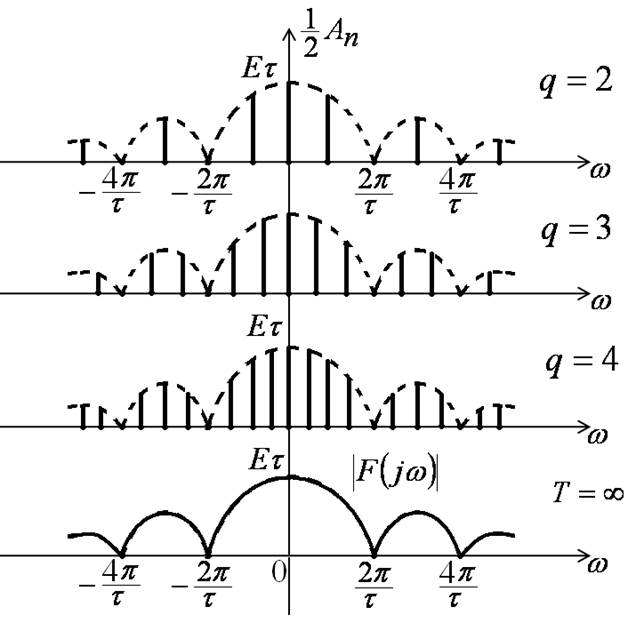
Связь дискретного и непрерывного спектров

Чтобы получить дискретный спектр периодического сигнала, нужно заменить в спектральной плотности непериодического сигнала частоту ω на nω1.
Тогда
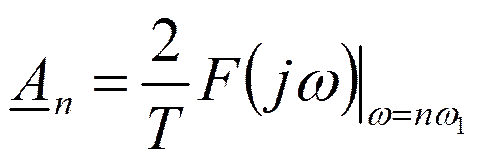
Например, для периодической последовательности прямоугольных импульсов
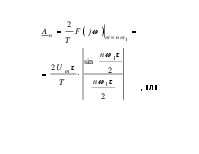
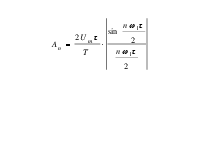
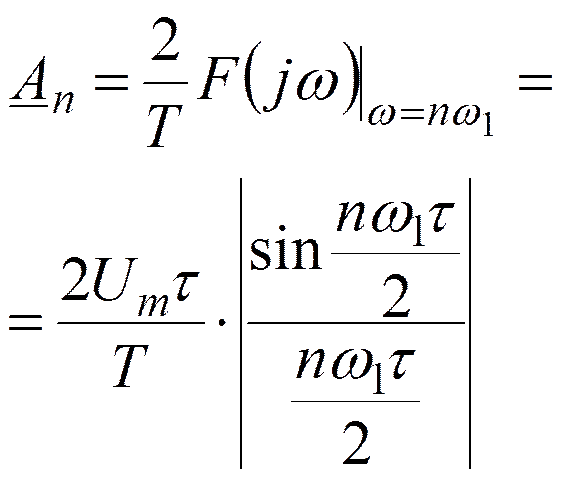 , или
, или
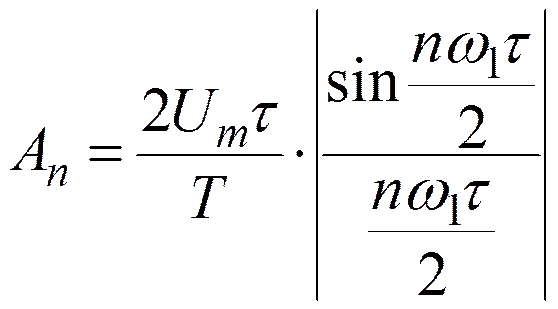

10.4. Одностороннее преобразование Фурье.
Связь с преобразованием
Лапласа
 |
При f(t)=0 для t<0
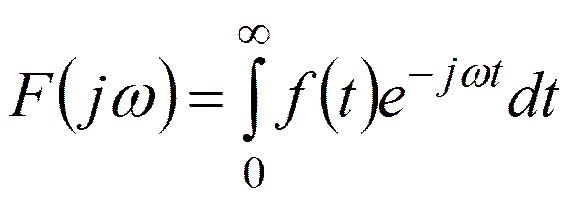
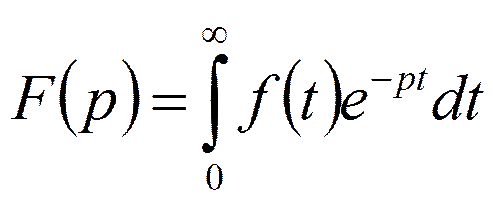
где р=a+jw.
При
α=0, т.е. при 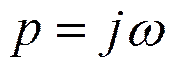 прямое
преобразование Лапласа переходит в прямое преобразование Фурье.
прямое
преобразование Лапласа переходит в прямое преобразование Фурье.
И
наоборот, при 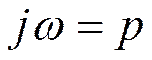 прямое
преобразование Фурье переходит в прямое преобразование Лапласа.
прямое
преобразование Фурье переходит в прямое преобразование Лапласа.
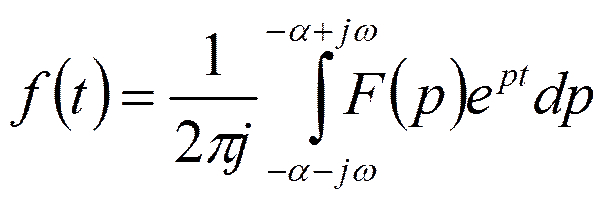
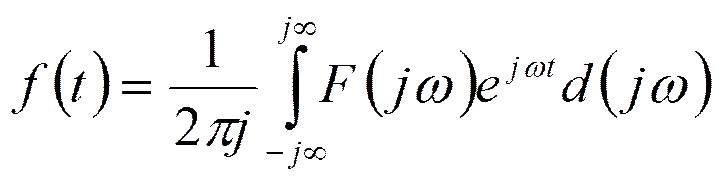
или
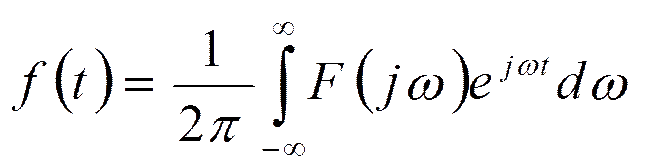
Таким
образом, при 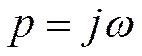 или
или 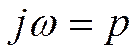 преобразования
Фурье и Лапласа переходят друг в друга.
преобразования
Фурье и Лапласа переходят друг в друга.
Для отыскания спектра можно использовать преобразование Лапласа.
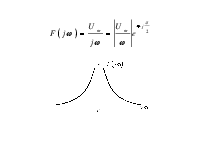
Спектр импульса включения (ступенчатого воздействия)

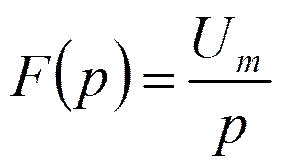
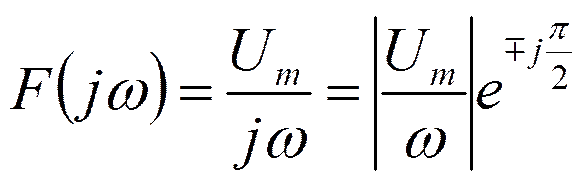
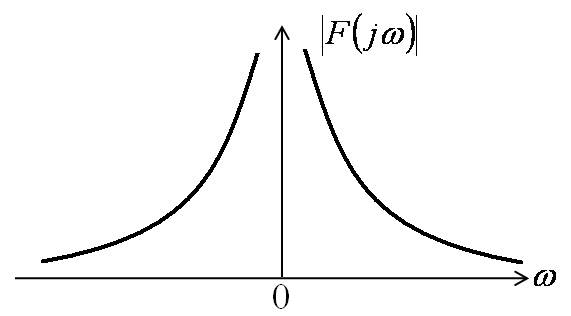
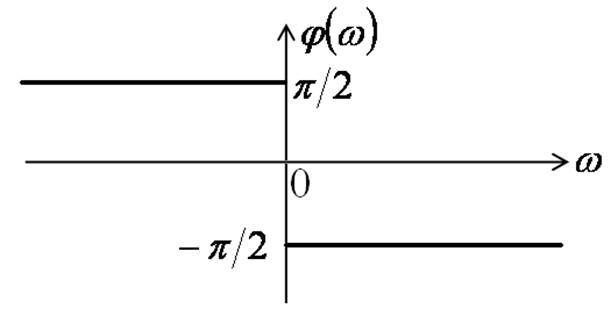
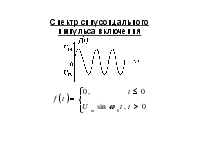
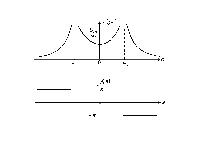
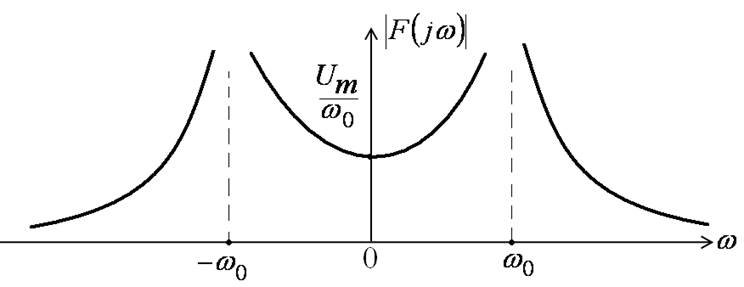
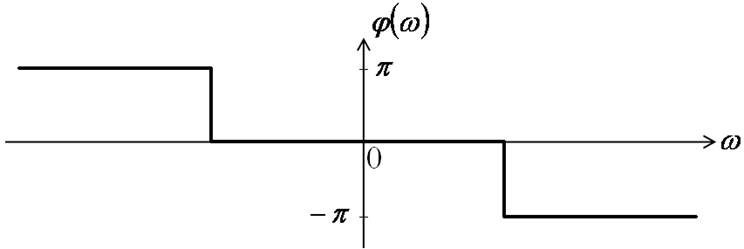
Спектр синусоидального импульса включения
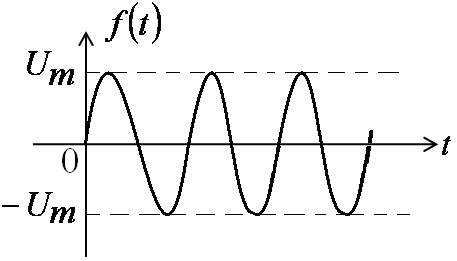
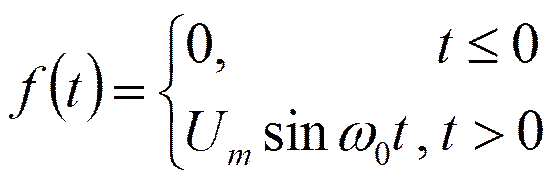
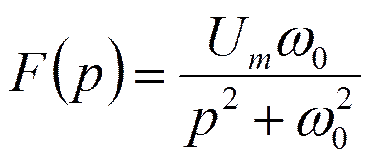

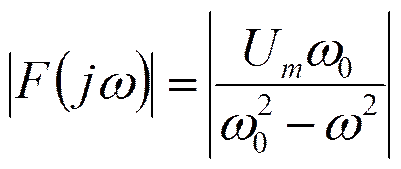
φ(ω)=0 при ω<ω0 ;
φ(ω)=![]() при ω>ω0
.
при ω>ω0
.
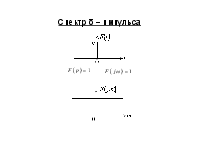
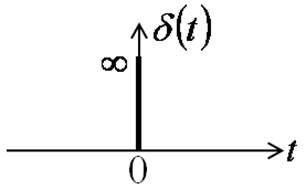
Спектр δ – импульса
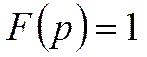
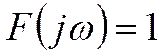
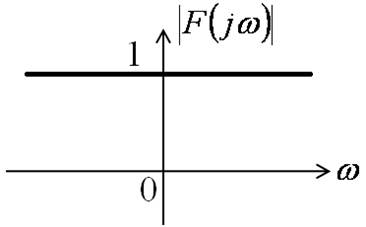
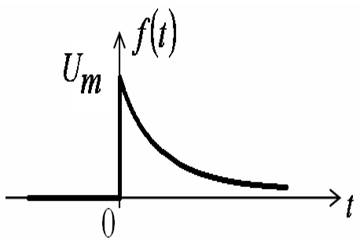
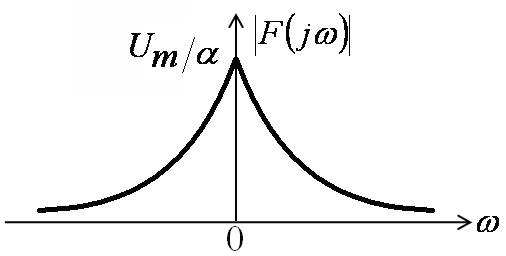
Спектр экспоненциального импульса
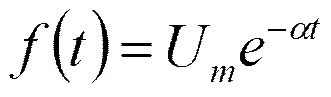
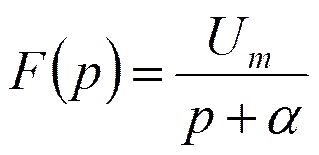

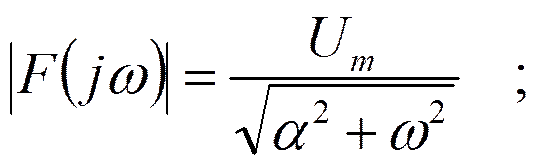
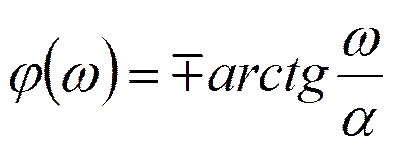
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.