Последовательное соединение R, L, C элементов при воздействии гармонического колебания. Закон Ома, Закон Кирхгофа. Активное, реактивное, полное сопротивление.
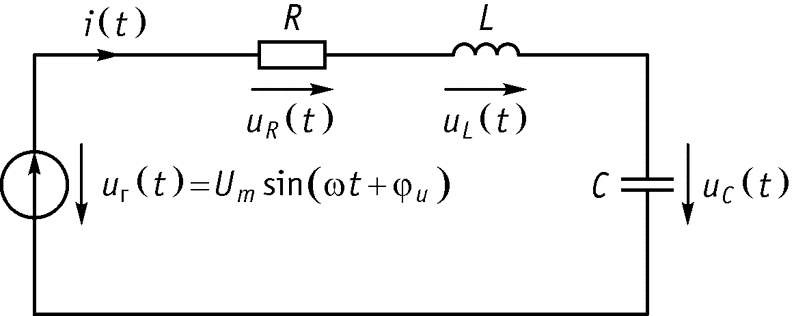
Пусть имеется электрическая схема, состоящая из последовательного соединения источника напряжения гармонических колебаний, резистивного сопротивления R, конденсатора С и индуктивности L. Закон Кирхгофа (ЗНК) для мгновенных значений
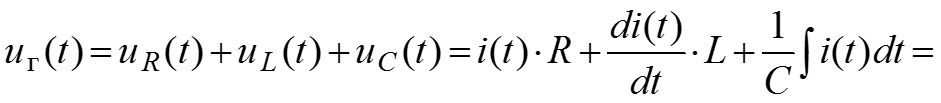
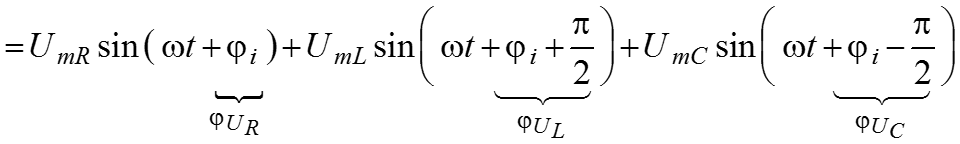
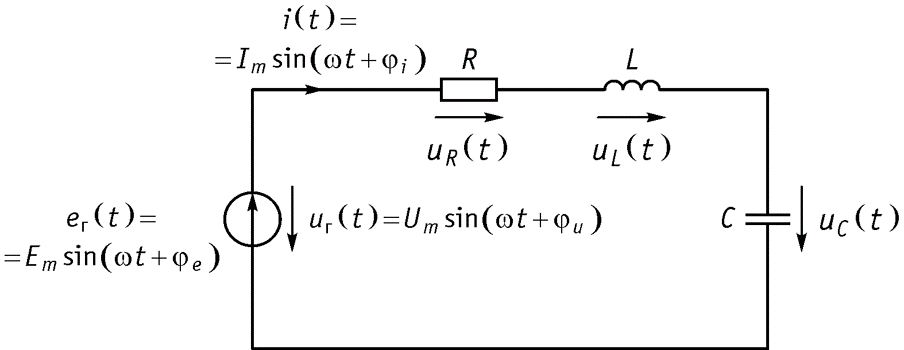
Из формулы видно, что фаза напряжения на сопротивлении совпадает с фазой тока
![]()
, протекающего через это сопротивление. Фаза напряжения на индуктивности, опережает на
![]()
![]()
фазу тока
![]()
от
Фаза напряжения на емкости отстает на
![]()
![]()
активная составляющая напряжения цепи -
![]()
напряжение на индуктивности –
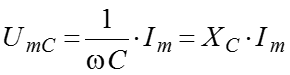
напряжение на емкости –
, [Ом]
![]()
индуктивное реактивное сопротивление –
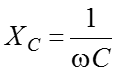
, [Ом]
емкостное реактивное сопротивление –
.
, [Ом]
![]()
реактивное сопротивление цепи –
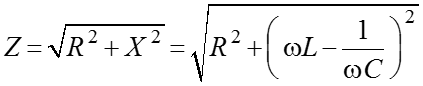
, [Ом]
полное сопротивление цепи – реактивная составляющая напряжения в цепи –
![]()
Закон Кирхгофа (ЗНК) для комплексных амплитуд Чтобы записать закон Кирхгофа для комплексных амплитуд необходимо перейти от мгновенных значений напряжения и тока к комплексной показательной форме напряжения и тока:
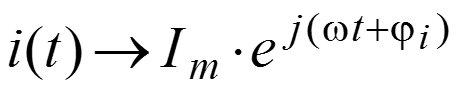
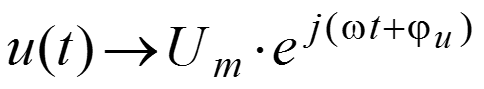
и подставить в уравнение ЗНК для мгновенных значений комплексные выражения
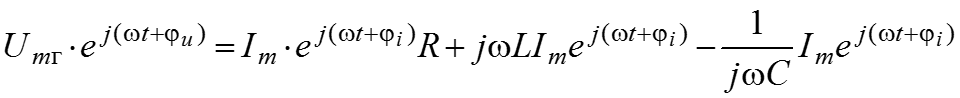
– закон Кирхгофа в комплексной форме.
![]()
– закон Ома в комплексной форме.
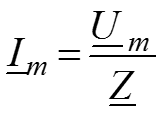
– комплексное сопротивление цепи.
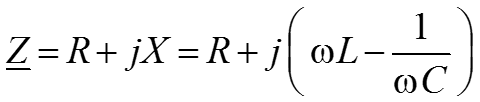
– индуктивное сопротивление в комплексной форме.
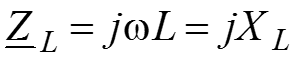
– комплексное емкостное сопротивление.
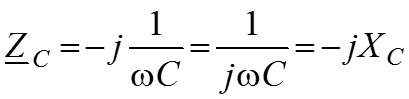
– комплексная проводимость цепи.
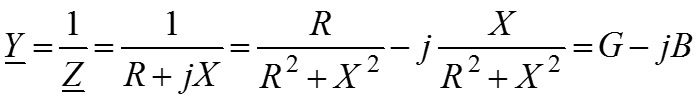
– активная проводимость;
![]()
– реактивное сопротивление.
Закон Кирхгофа для комплексных действующих амплитуд
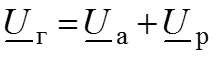
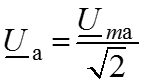
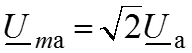
Закон Ома для комплексных действующих амплитуд
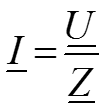
ЗНК и ЗТК в общем виде
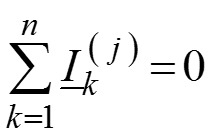
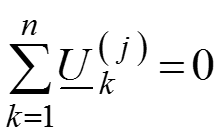
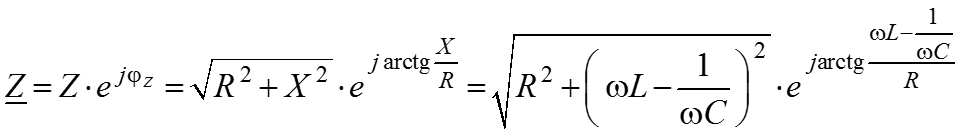
Параллельное соединение R, L, C Рассмотрим схему, приведенную на рисунке
Обозначим токи.
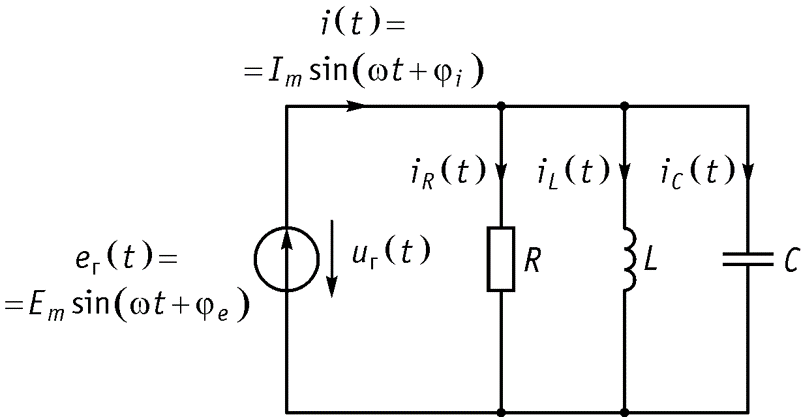
Закон токов Кирхгофа для мгновенных значений
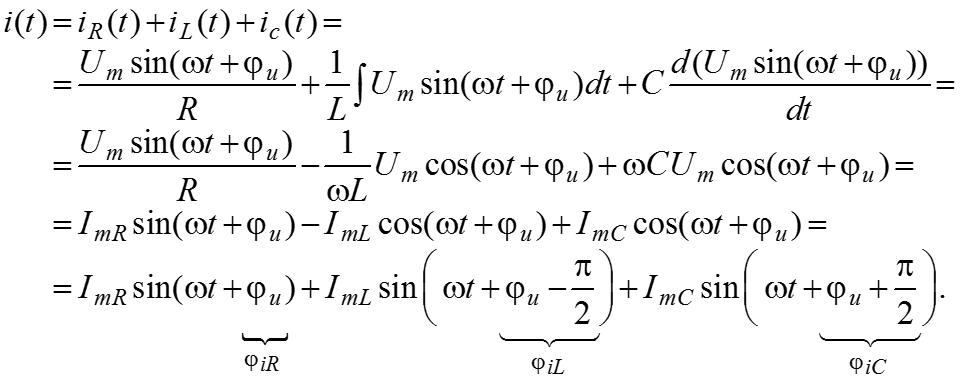
– активная составляющая тока в цепи
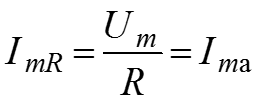
– реактивная составляющая тока в цепи.
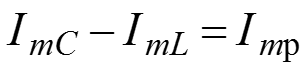
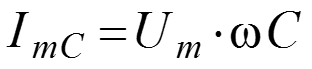
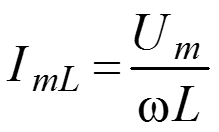
.
ЗТК для комплексных амплитуд
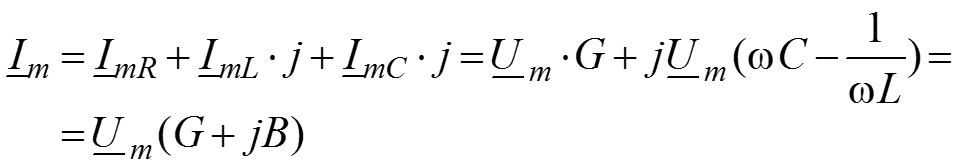
![]()
– закон Ома для комплексных амплитуд
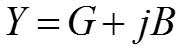
– комплексная проводимость цепи
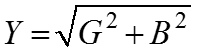
– полная проводимость
![]()
– активная проводимость цепи;
![]()
– реактивная проводимость цепи.
Единицы измерения [См] – сименсы.
Смешанное соединение R, L, C Пусть задана схема, приведенная на рисунке, а. Определим только комплексные сопротивление ветвей ( )
![]()
и комплексное сопротивление цепи относительно зажимов а и b (рис. б).
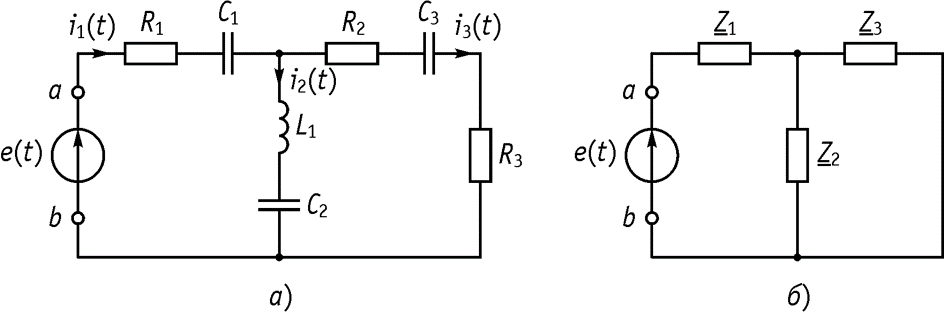
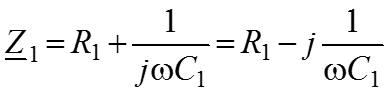
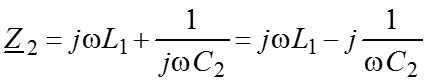
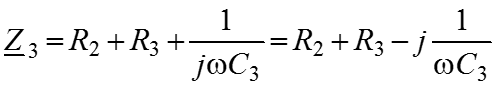
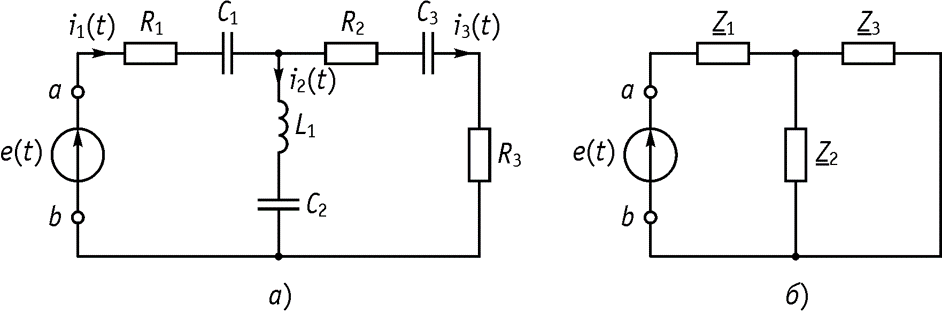
Тогда сопротивление ab .
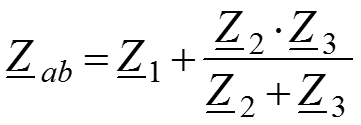
Необходимо подставить вместо
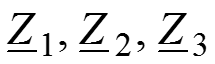
их выражения через элементы схемы и преобразовать так, чтобы получить реальную формулу, состоящую из
![]()
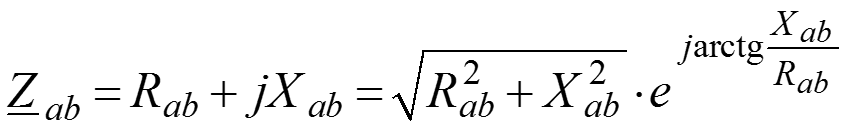
.
.
Методы расчета линейных электрических цепей при воздействии гармонических колебаний
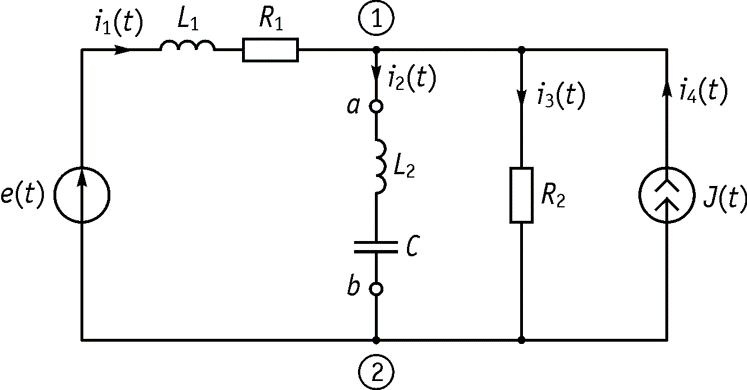
При гармоническом воздействии используются те же методы расчета, что и при расчете линейных цепей при постоянном токе: свертывание, метод контурных токов, ЗТК и ЗНК, узловых потенциалов, метод эквивалентного генератора, метод наложения. Мы рассмотрим три метода. Метод законов Кирхгофа. Пусть имеется электрическая схема, приведенная на рисунке 43. Определить токи и напряжения.
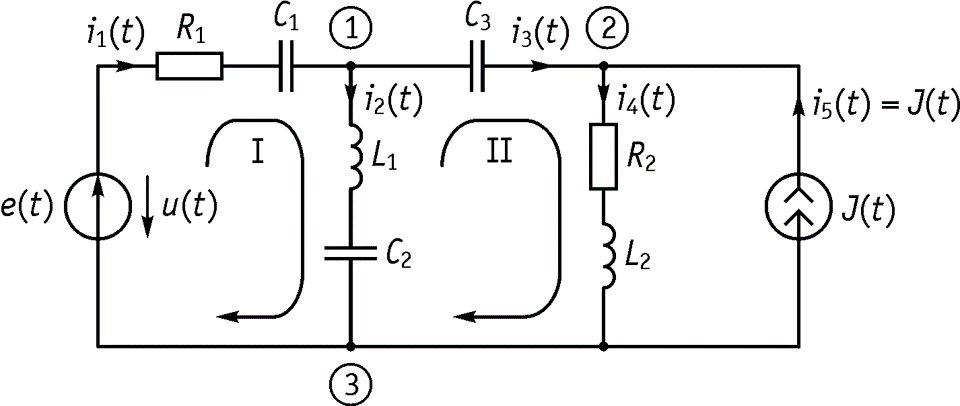
Алгоритм метода: 1. Обозначаем узлы. 2. Выбираем токи.
3. Выбираем независимые контуры и выбираем направление обхода контура (произвольно). 4. Записываем ЗТК для комплексных амплитуд
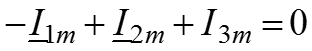
– для узла 1;
![]()
– для узла 2.
5. Записываем ЗНК для 1-го и 2-го контуров 1й контур:
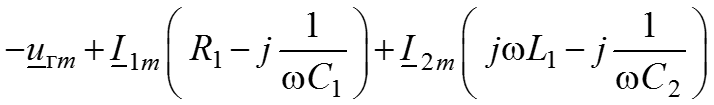
2й контур:
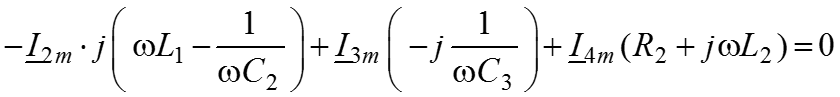
6. Решаем совместно, полученную систему ЗТК и ЗНК относительно неизвестных токов
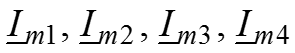
7. После нахождения токов и напряжений для комплексных амплитуд, переходим к мгновенным, реальным значениям токов и напряжений
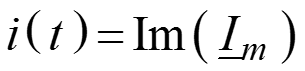
– если sin в Е.
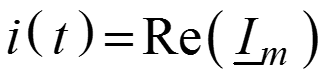
– если cos в Е.
СТР.37
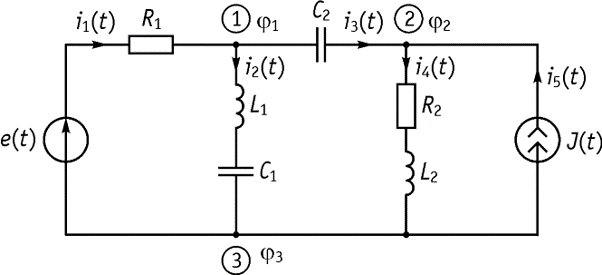
Метод узловых напряжений. Пусть имеется электрическая схема, приведенная на рисунке 44. Алгоритм анализа: 1. Обозначим узлы и их потенциалы. 2. Обозначаем токи.
3. Выбираем базисный узел (поскольку в схеме нет идеального источника напряжения, следовательно, можно выбрать любой). Мы выбираем
![]()
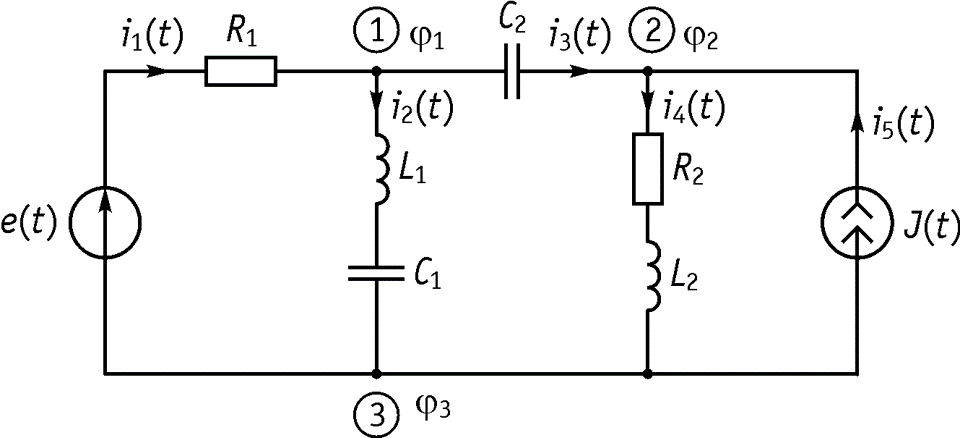
4. ЗТК для комплексных амплитуд 1 узел:
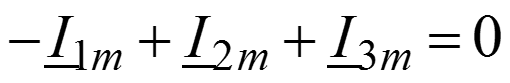
2 узел:
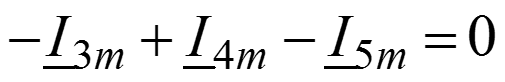
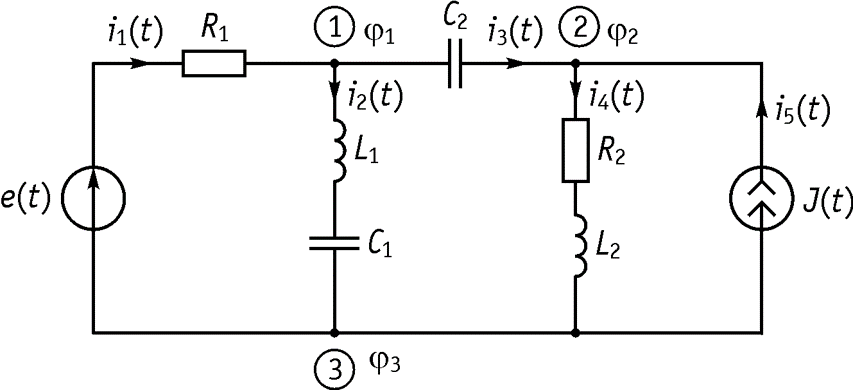
5. Найдем токи в ветвях для комплексных амплитуд через узловые потенциалы, используя закон Ома для участка цепи
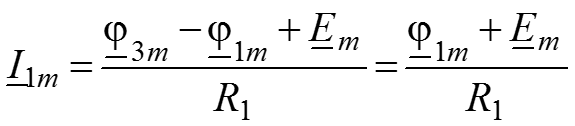
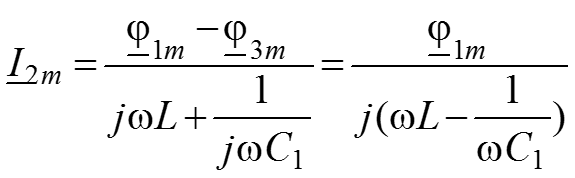
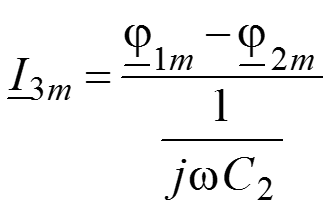
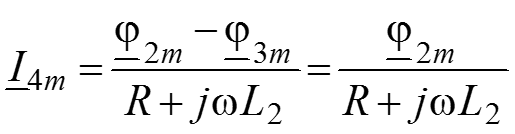
6. Подставим полученные уравнения для токов в ЗТК
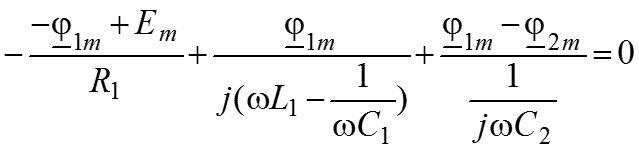
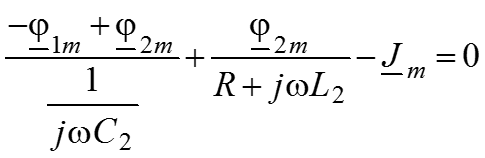
7. Решаем полученную систему уравнений
.
8. Зная потенциал, определяем токи, зная токи, определяем напряжения. 9. Переходим от комплексного представления напряжений и токов, к мгновенным значениям по формулам, приведенным раньше.
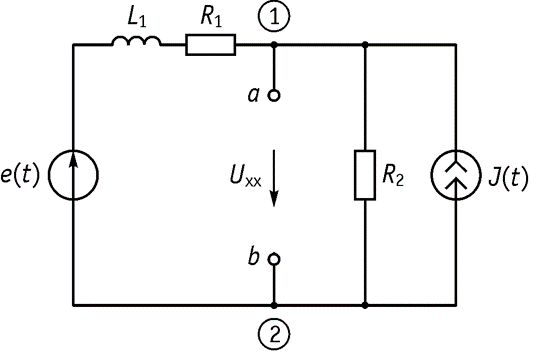
Метод эквивалентного генератора. Пусть имеется электрическая схема, приведенная на рисунке. Алгоритм решения: 1. Обозначаем узлы. 2. Обозначаем токи в ветвях. 3. Удаляем из схемы
![]()
и С, напряжение между зажимами а и б обозначаем, как
![]()
(напряжение холостого хода) и направляем его по направлению тока . 4. Возьмем любой контур, в который входит
![]()
(кроме контура с источником тока
). Запишем ЗНК
![]()
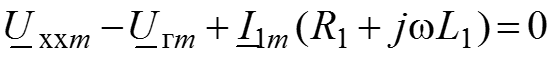
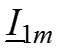
5. Находим
Для этого составим ЗНК и ЗТК
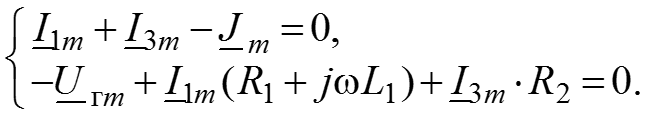
Решаем совместно уравнение относительно
![]()
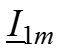
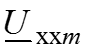
6. Зная
, определяем
7. Определяем относительно аb эквивалентное комплексное сопротивление цепи.
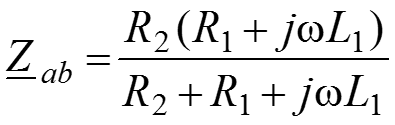
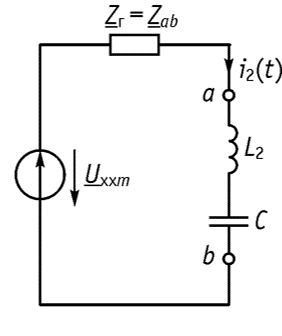
8. Определяем ток, протекающий через индуктивность L2 и емкость С
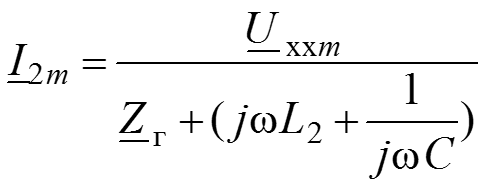
.
Мгновенная, средняя, реактивная, комплексная и полная мощности в электрической цепи при гармоническом воздействии Пусть имеется схема, состоящая из последовательно соединенного источника напряжения и элементов R, L, C .
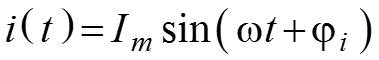
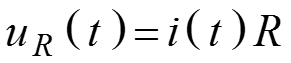
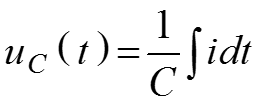
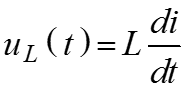
Мгновенная мощность
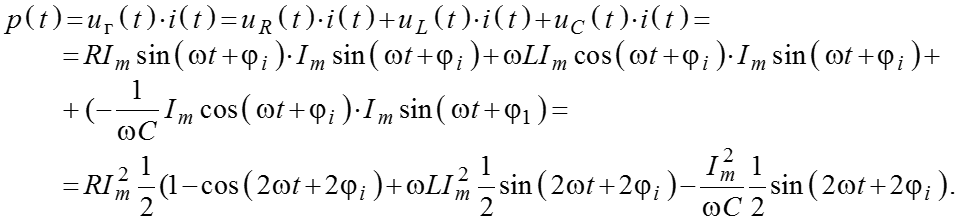
Комплексная мощность в цепи
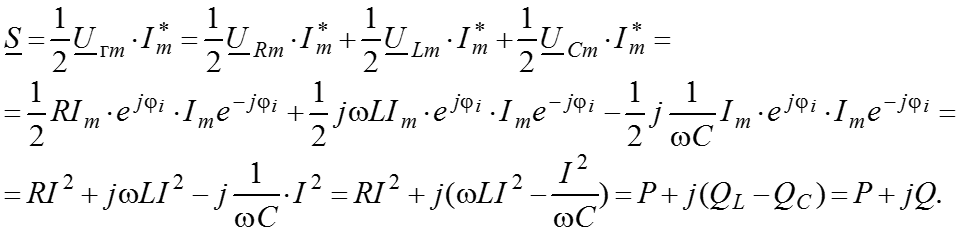
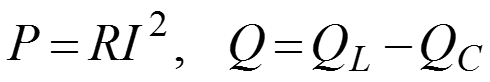
(ВАР – вольтампер реактивный).
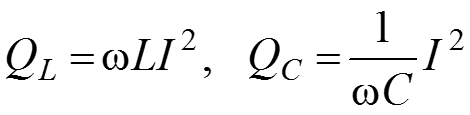
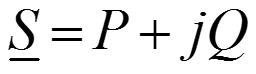
, [ВА].
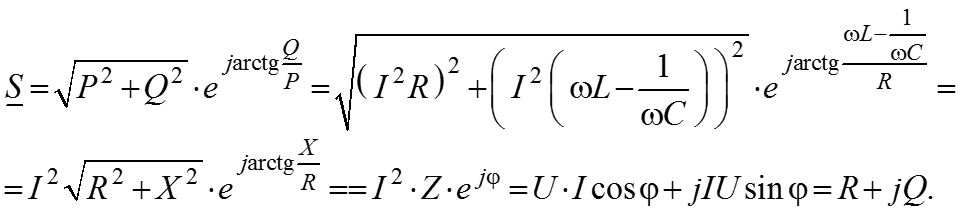
– коэффициент мощности, характеризует потери при передачи энергии. Чем больше
![]()
, тем меньше потери в линии передачи.
![]()
Модуль комплексной мощности равен полной мощности.
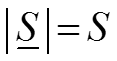
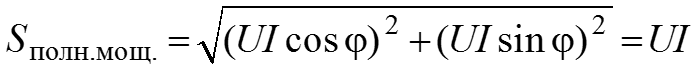
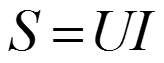
– полная мощность.
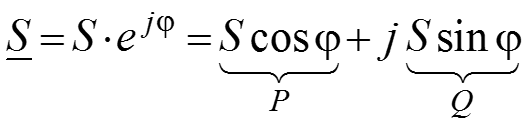
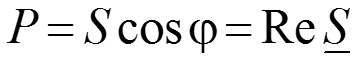
– активная мощность,
– реактивная мощность.
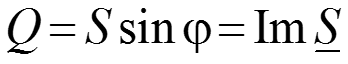
Условия передачи максимальной активной мощности от источника напряжения в комплексную нагрузку Пусть имеется схема, приведенная на рисунке.
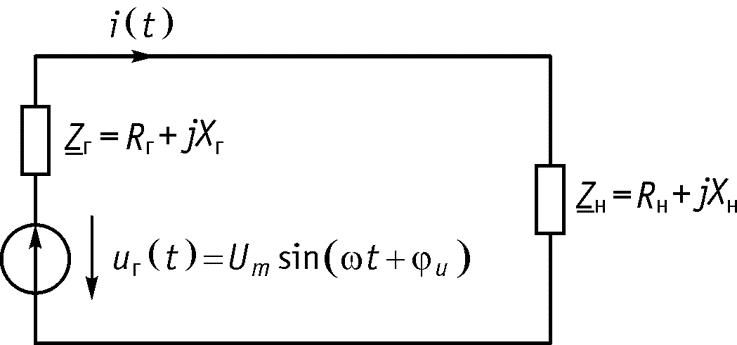
Чтобы от источника напряжения в комплексную нагрузку передавалась максимальная мощность, должны выполняться условия
.
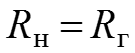
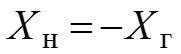
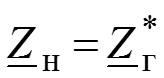
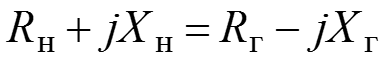
или т.е. необходимо выполнения
Баланс мощности в электрической цепи при гармоническом воздействии
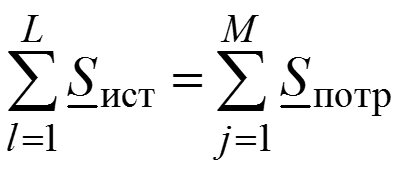
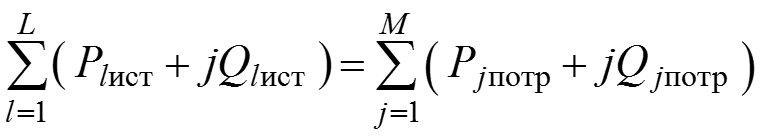
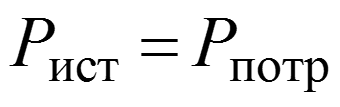
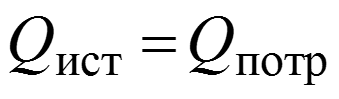
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.