Нелинейные цепи. Нелинейные элементы и их характеристики. Нелинейные цепи при постоянном воздействии

Последовательное соединение нелинейного и линейного элементов

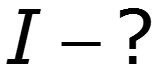
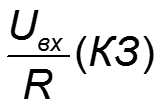
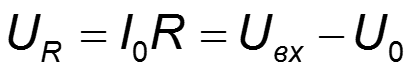
- напряжение на R

2. Последовательное соединение нелинейных элементов

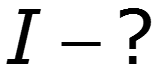
3. Параллельное соединение нелинейных элементов

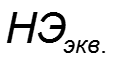
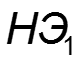
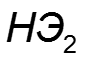
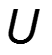
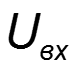
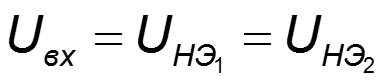
4. Смешанное соединение нелинейных элементов

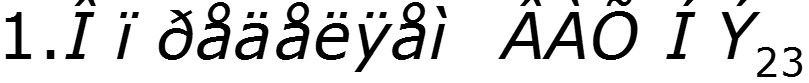
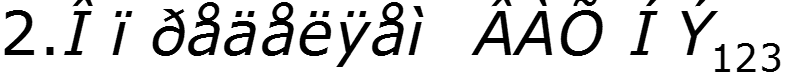
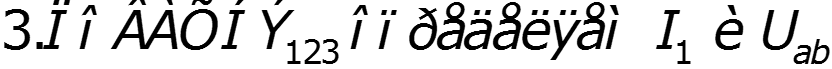
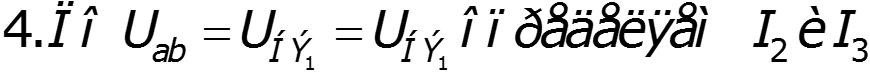
5. Расчет сложной цепи с одним нелинейным элементом (метод эквивалентного генератора)

Порядок расчета а) Обозначить токи в ветвях б) Выделить зажимы ab, к которым подключен нелинейный элемент и удалить его в) используя законы Кирхгофа, определить

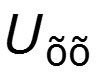
г) Определить эквивалентное сопротивление относительно зажимов аb при удаленных источниках д) Представляем схему эквивалентного генератора и подключим к зажимам генератора ab нелинейный элемент е) На графике ВАХ построить нагрузочную прямую и определить ток и напряжение на нелинейном элементе ж) По законам Ома и Кирхгофа найти токи на линейных элементах цепи

Пример

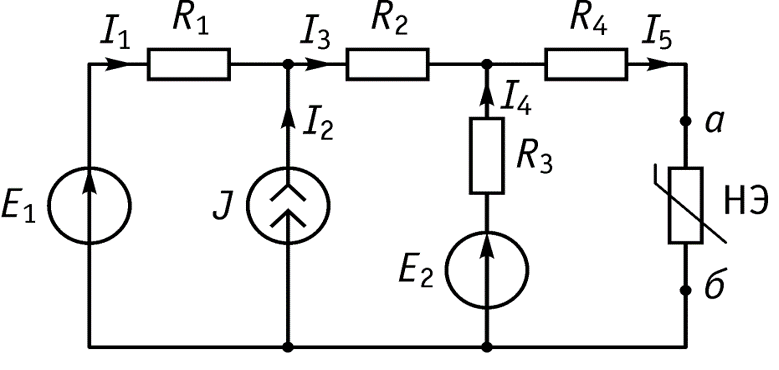
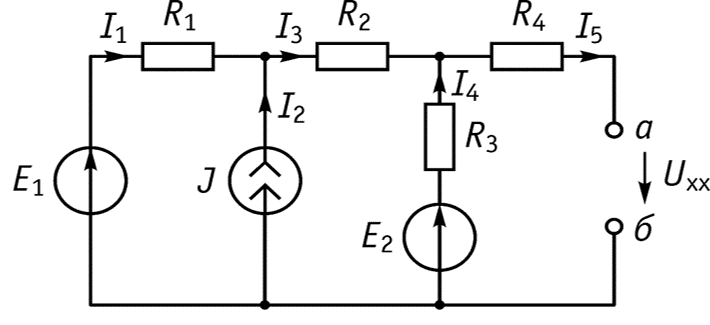
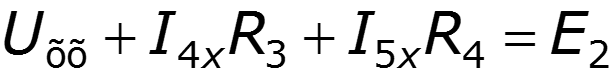
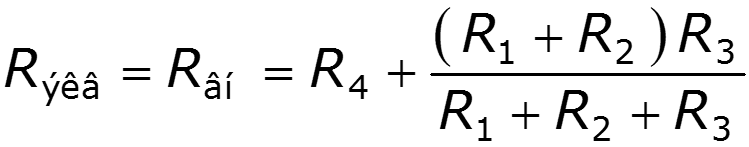
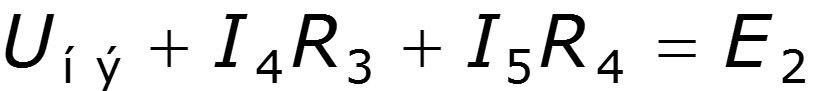
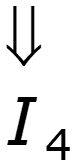
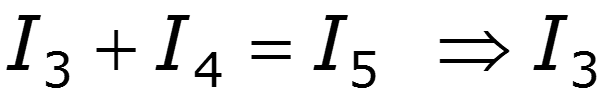
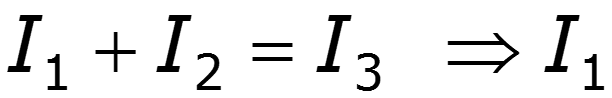
Аналитические методы – ВАХ нелинейного элемента задана аналитически

Пример

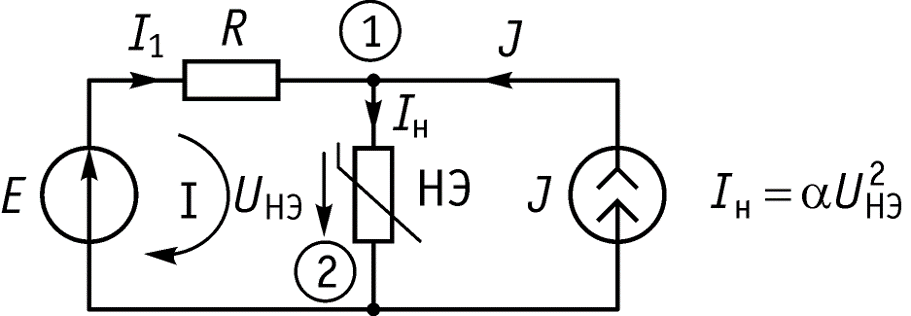
Рассчитаем схему по законам Кирхгофа

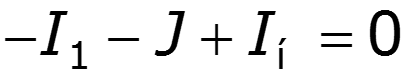
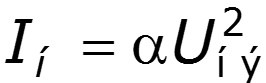
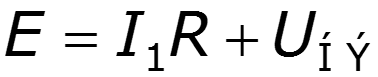
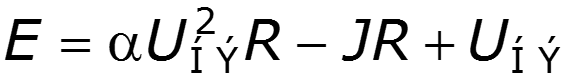
11.3 Нелинейный элемент в цепи переменного тока

Постановка задачи: на вход нелинейного элемента (НЭ) подается сумма напряжений: постоянного и гармонического, т.е.

• Найти:
• закон изменения тока на НЭ
• спектр тока

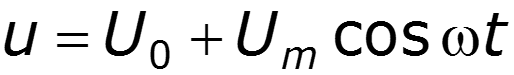
i

i

р.т.

U

ωt

ωt

ток i(t) - периодическая функция времени, которая может быть представлена рядом Фурье:

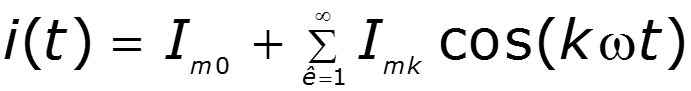
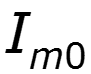
- постоянная составляющая

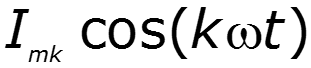
- гармоники

Спектр тока в НЭ при гармоническом воздействии является дискретным

Аналитические методы вычисления спектра тока через нелинейный элемент основаны на аппроксимации ВАХ Аппроксимация – представление функции, заданной таблично или графически, в аналитическом виде, т.е. в виде формулы

Этапы аппроксимации

1. Выбор класса функций, которыми аппроксимируется характеристика
2. а) степенной полином
3. б) кусочно-линейная (отрезки прямых)
4. в) экспонента
5. г) гиперболический тангенс

2. Определение коэффициентов аппроксимации а) метод интерполяции (метод выбранных точек) б) метод Тейлора в) метод Чебышева г) метод среднеквадратического приближения

11.4 Полиномиальная аппроксимация

Применяется для точного воспроизведения ВАХ при работе с сигналами малой амплитуды Пусть функция задана графически или таблично Найдем аппроксимирующую функцию

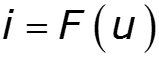
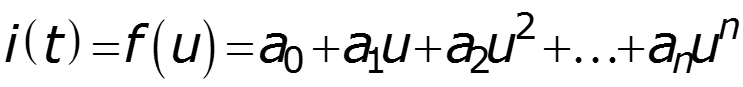
При работе с напряжениями малой амплитуды нет необходимости аппроксимировать всю ВАХ Достаточно выполнить аппроксимацию в окрестностях рабочей точки Степень полинома выбирают по виду рабочего участка

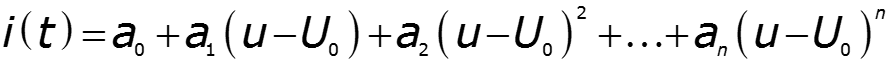
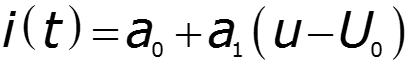
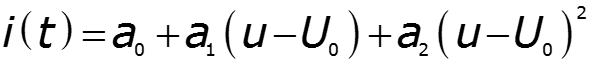
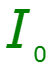
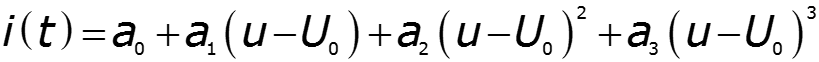
Обычно

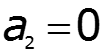
Спектр тока при полиномиальной аппроксимации

Пусть ВАХ НЭ выражается полиномом 5 степени

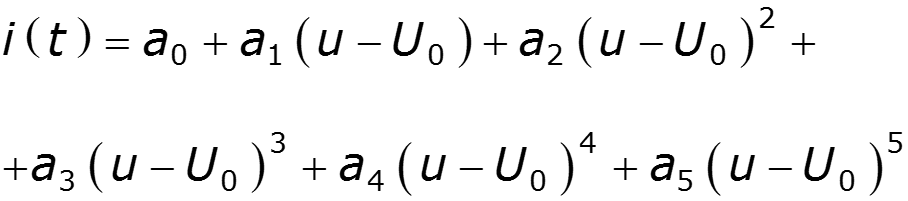
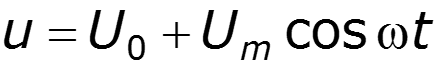
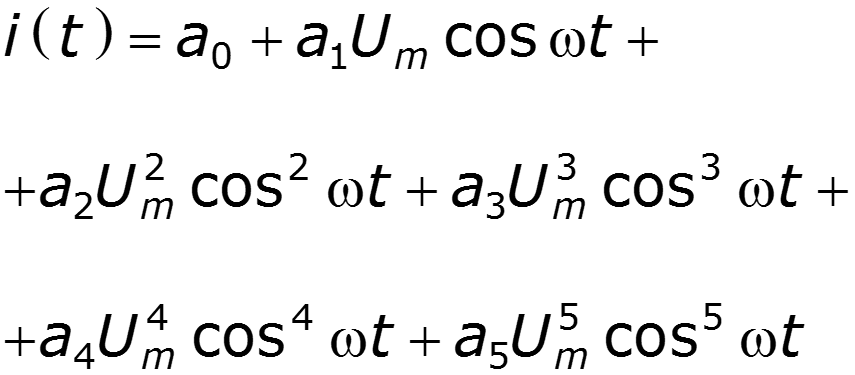
Формулы понижения степени:

• Выводы:
• Нелинейность ВАХ НЭ приводит к искажению формы сигнала и изменению его спектра.
• Число гармоник тока определяется степенью аппроксимирующего полинома.

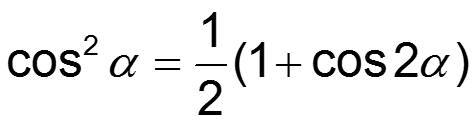
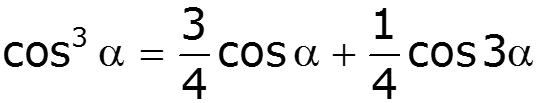
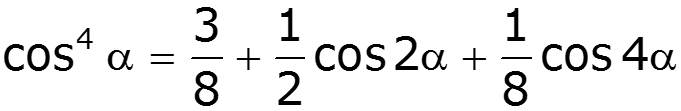
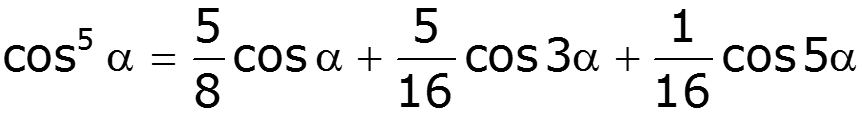
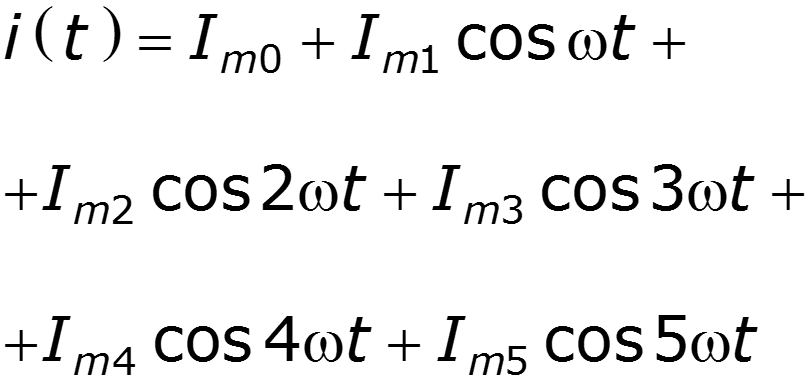
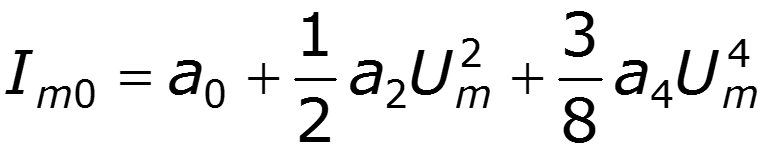
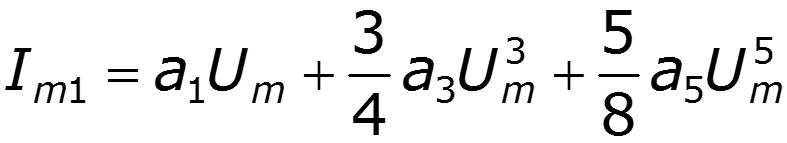
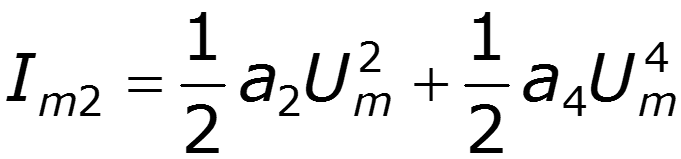
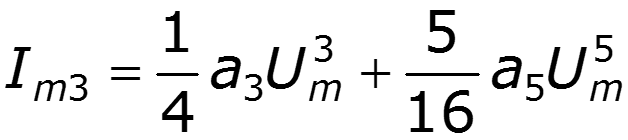
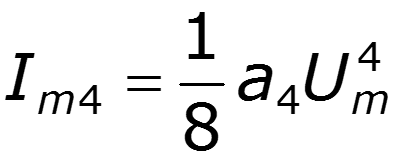
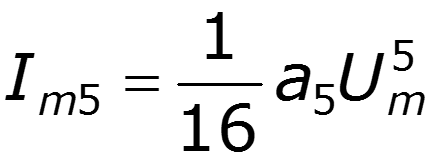
3) Постоянная составляющая и четные гармоники определяются четными членами полинома 4) Амплитуды нечетных гармоник зависят от коэффициентов при нечетных степенях

Выбирая при аппроксимации степень полинома мы, тем самым, задаем ширину спектра выходного сигнала

Определение коэффициентов методом интерполяции

1. Выбираем узлы интерполяции
2. Число узлов интерполяции n+1 - на 1 больше степени полинома
3. Функции F(u) и f(u) в узлах интерполяции совпадают

Пример

Постановка задачи: Дана ВАХ НЭ:

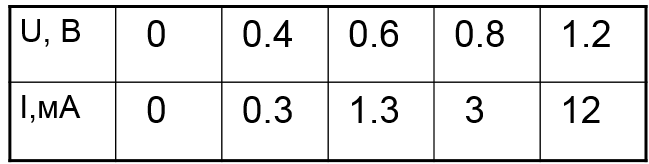
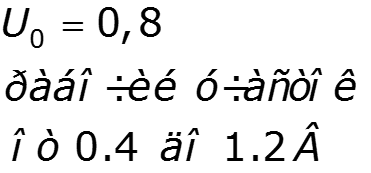
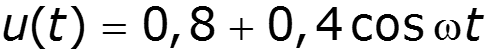
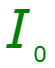
Полином второй степени

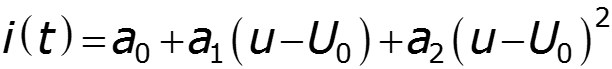
Составим систему уравнений:

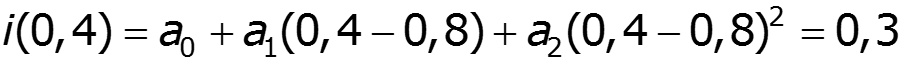
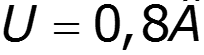
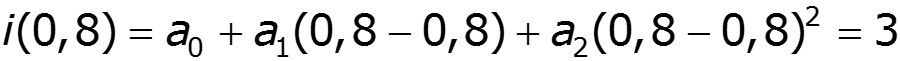
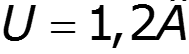
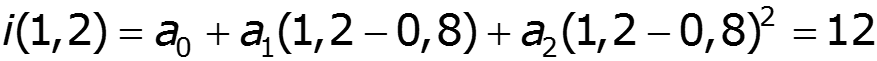
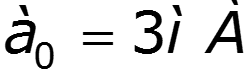
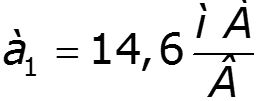
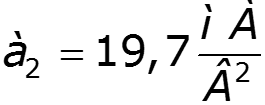
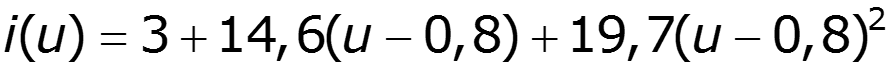
спектр выходного тока:

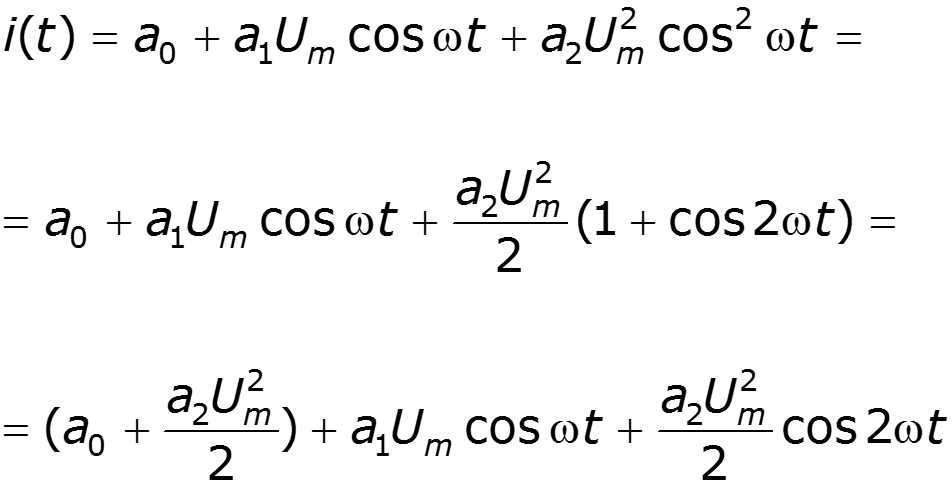
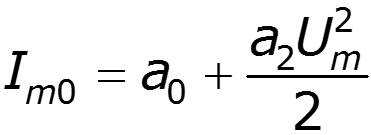
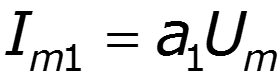
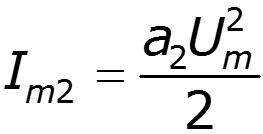
Аппроксимация рядом Тейлора

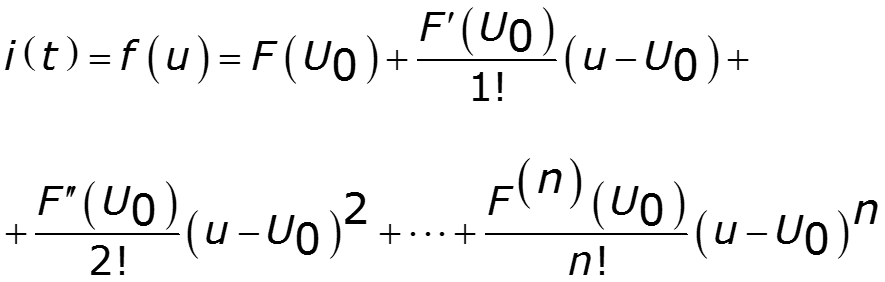
Позволяет перейти к степенному полиному от более сложной функции

Пример

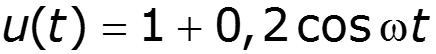
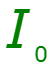
Полином первой степени

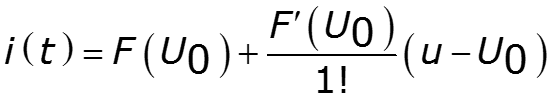
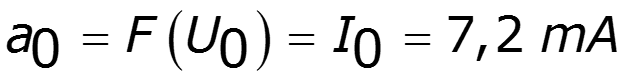
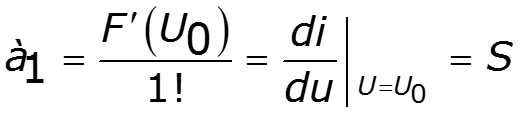
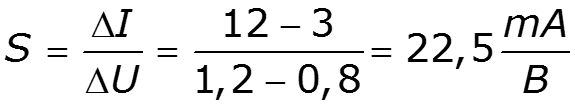
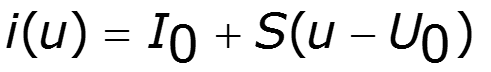
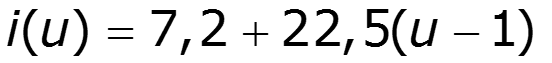
спектр выходного тока:

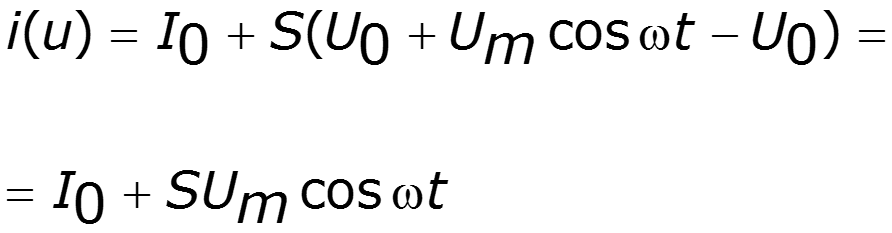
При аппроксимации полиномом первой степени форма выходного тока НЭ повторяет форму входного сигнала

11.5 Кусочно-линейная аппроксимация

Замена ВАХ отрезками прямых линий, образующих в интервале аппроксимации непрерывную функцию f(x). Применяется, когда размах входного сигнала на НЭ уходит либо в зону насыщения, либо в зону отсечки. Для данной аппроксимации используют полином 1-й степени.

где: напряжение отсечки напряжение насыщения ток насыщения рабочая точка

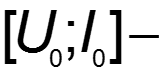
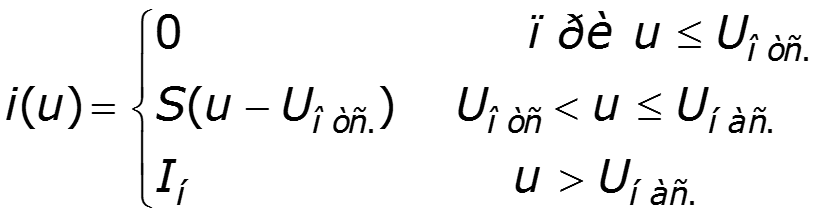
S – крутизна полученной ВАХ в области измерения тока НЭ

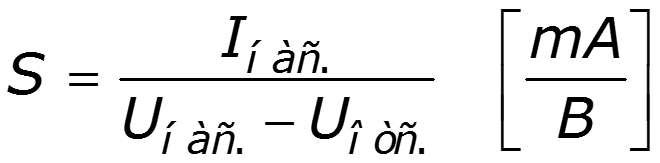
Пример ВАХ НЭ:

Проведем касательную к линейной части ВАХ и определим напряжение отсечки:

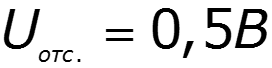
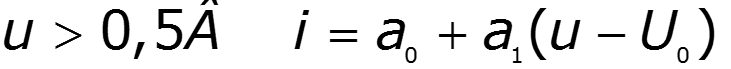
По методу Тейлора:

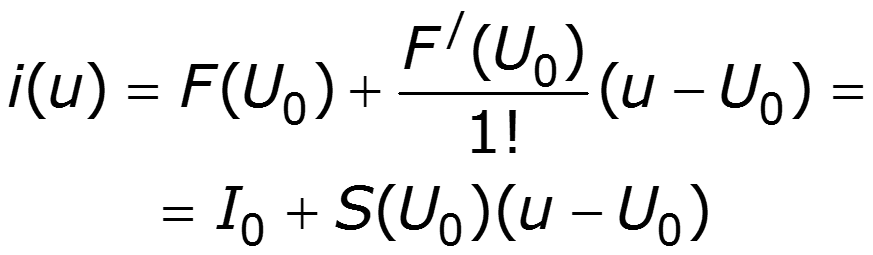
Пусть

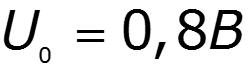
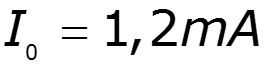
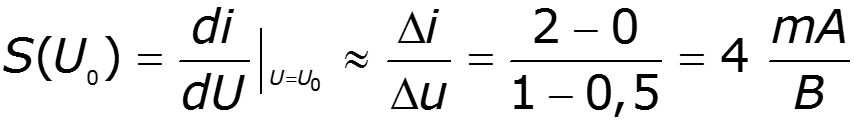
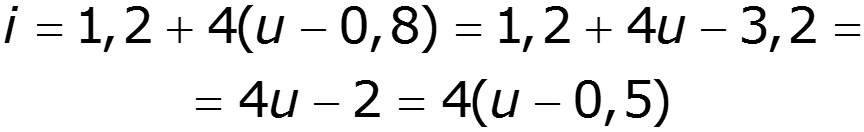
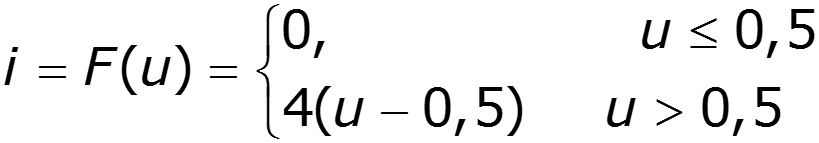
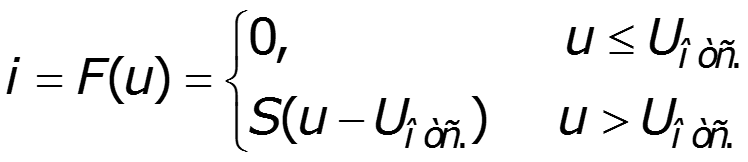
Спектр выходного тока при кусочно-линейной аппроксимации (метод угла отсечки)

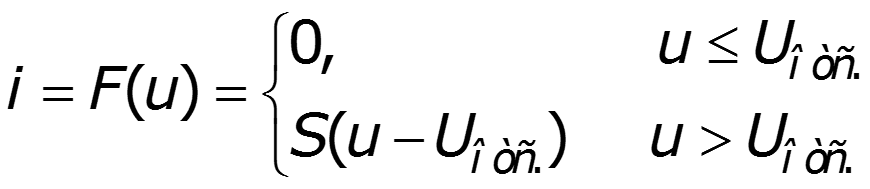
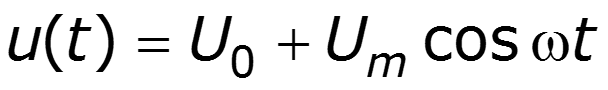
Часть полупериода ( в координатах ), в течение которого существует ток в цепи нелинейного элемента, называется углом отсечки Диапазон изменения угла отсечки

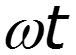
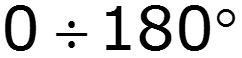
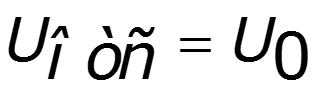
Величина угла отсечки не зависит от амплитуды приложенного напряжения