9. Временной метод анализа электрических цепей
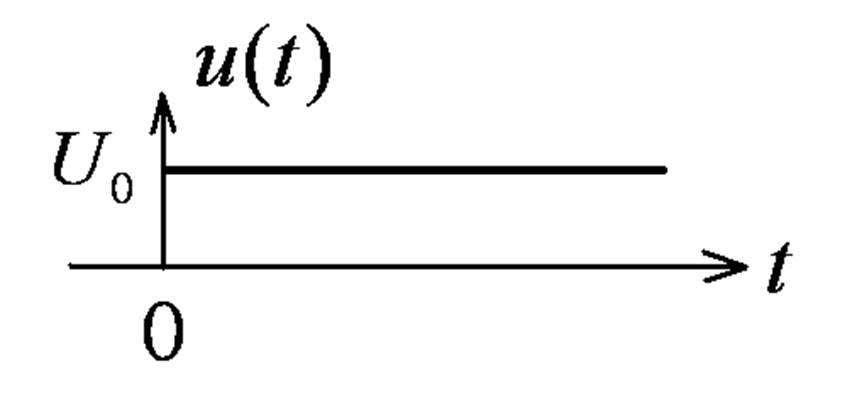
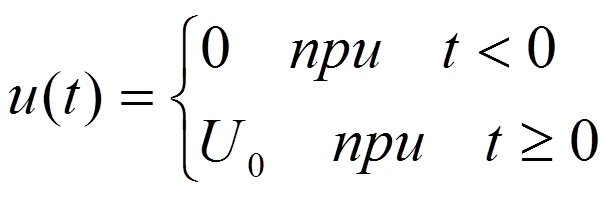
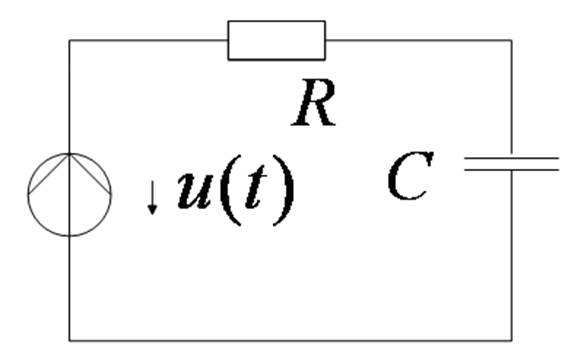

Реакция цепи - 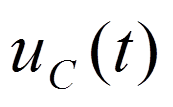
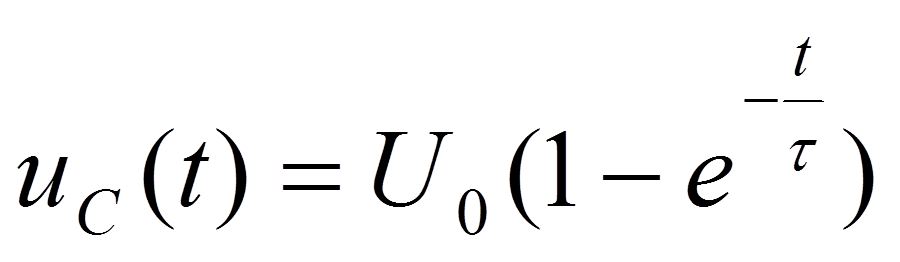 при t ≥ 0.
при t ≥ 0.
Реакция цепи – 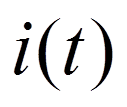
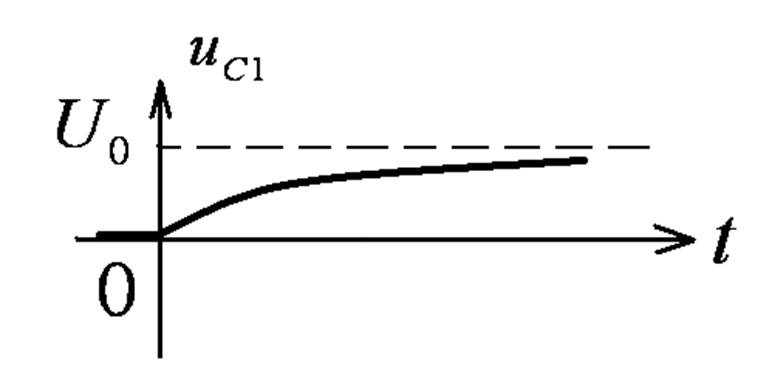
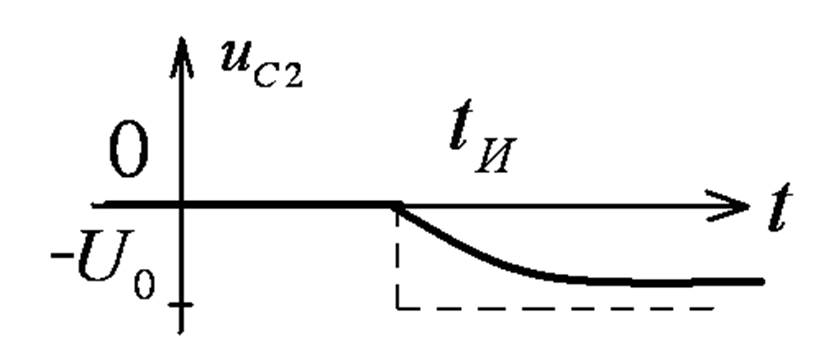
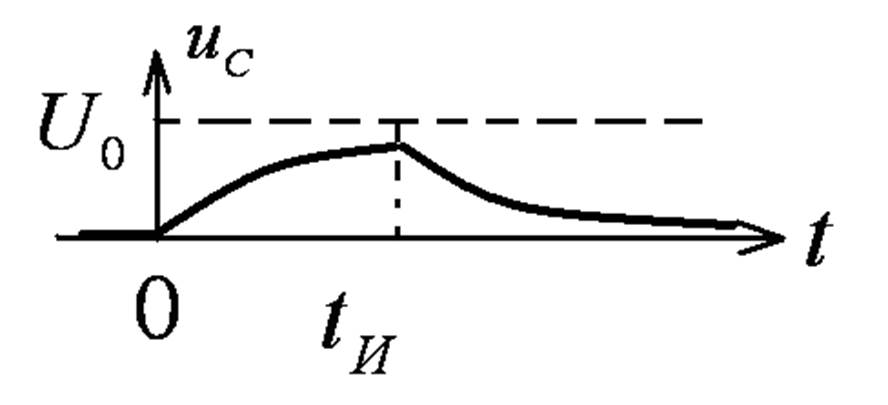
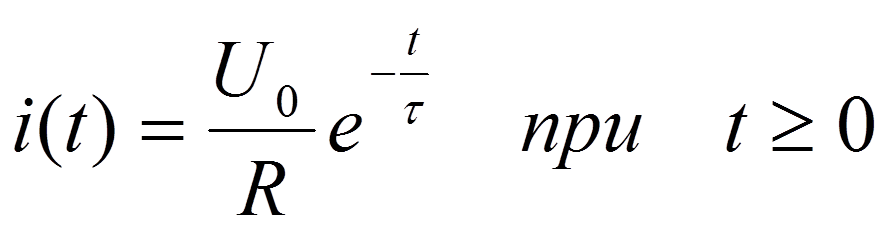 Прямоугольный импульс
Прямоугольный импульс
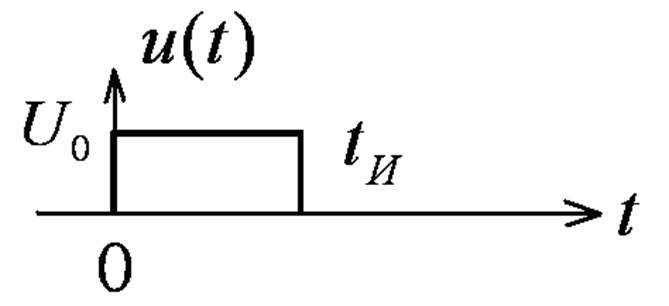
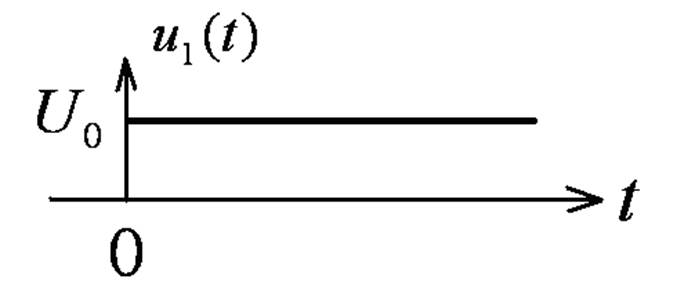
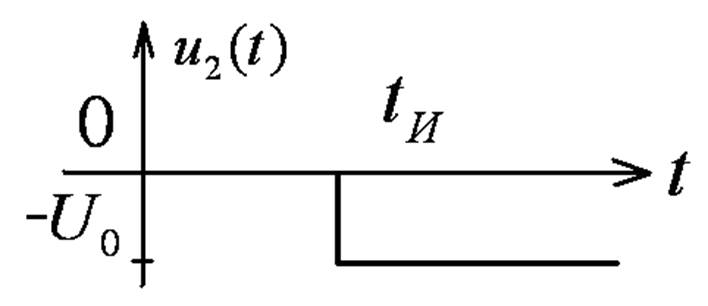

На интервале 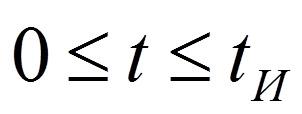
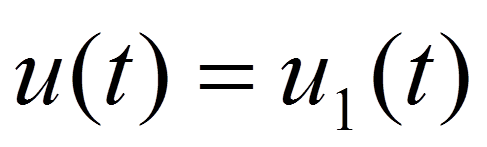
На интервале 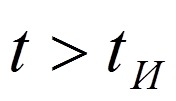
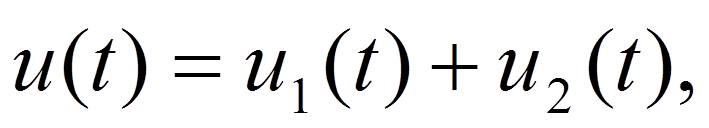
но 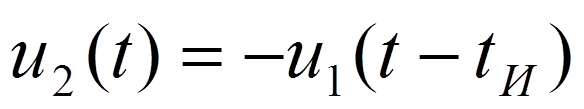
поэтому 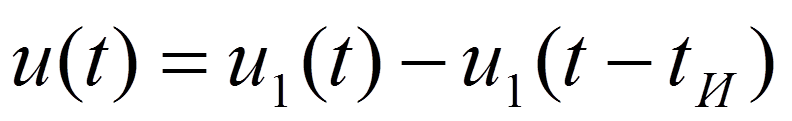
реакция цепи - 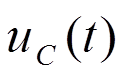
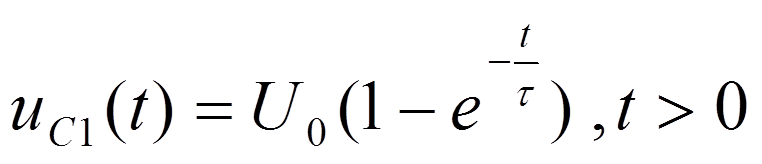
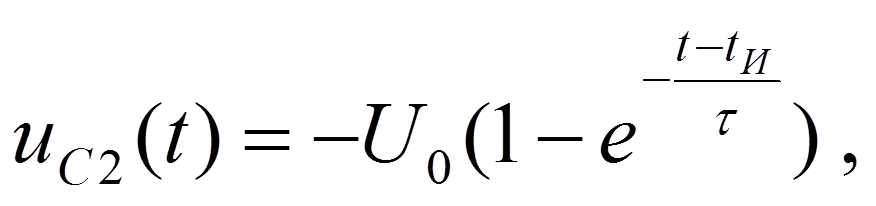
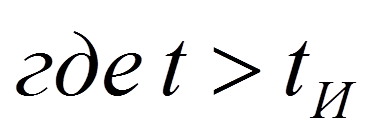
В интервале 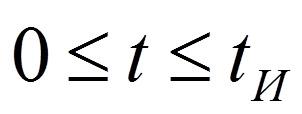
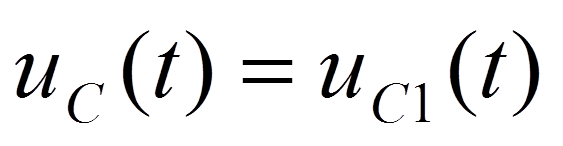
В интервале 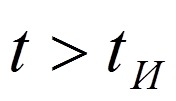
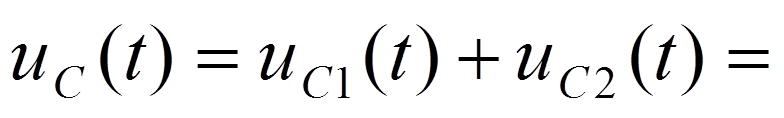
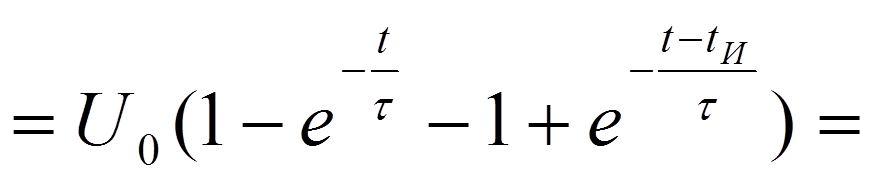
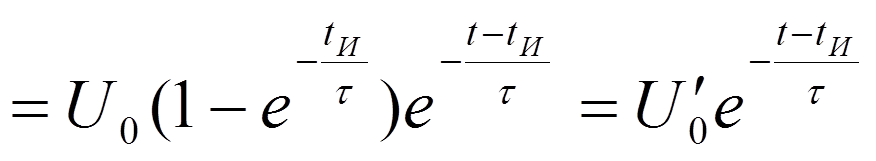
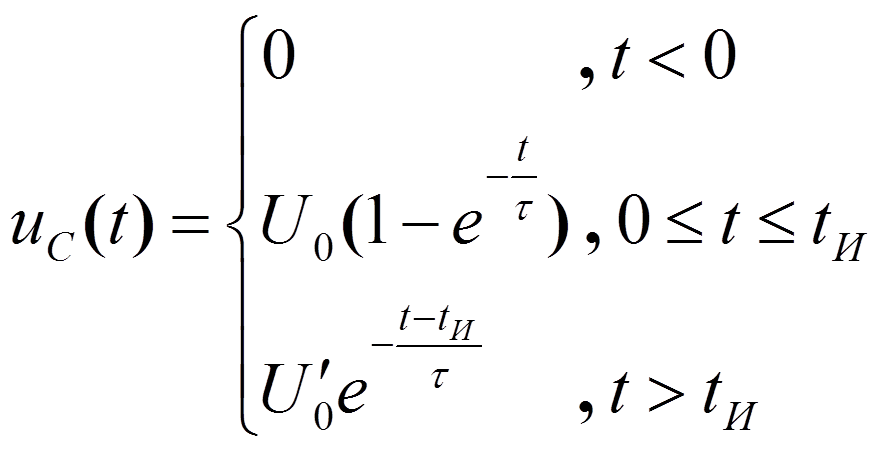

9.1. Переходные характеристики цепи
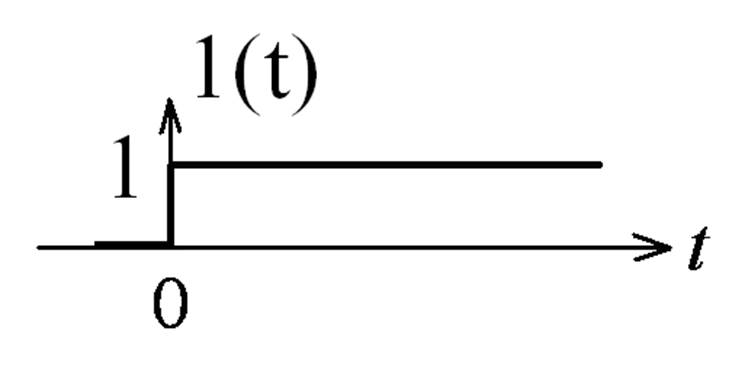
Ступенчатое воздействие
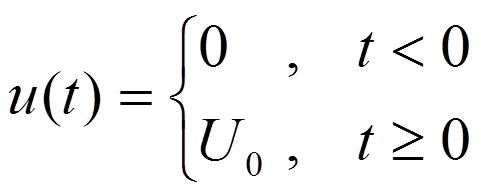
Переходная характеристика – реакция цепи на единичное ступенчатое воздействие 1(t).
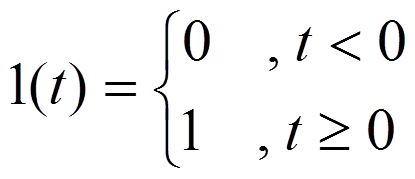
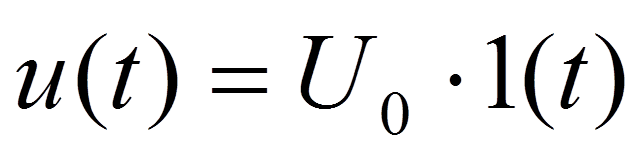
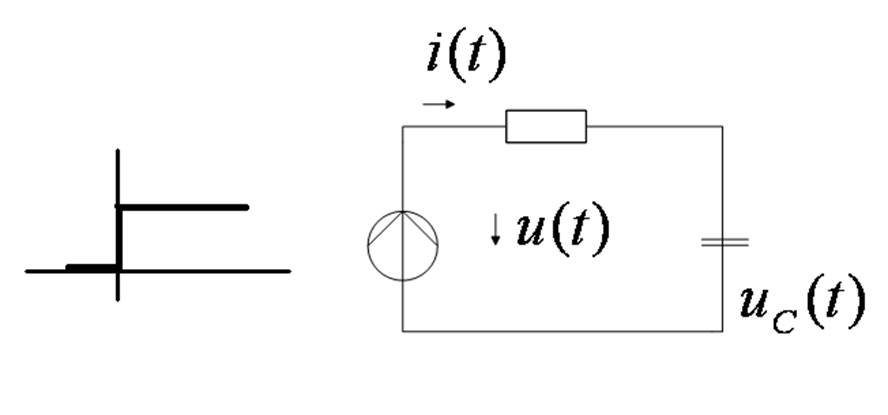
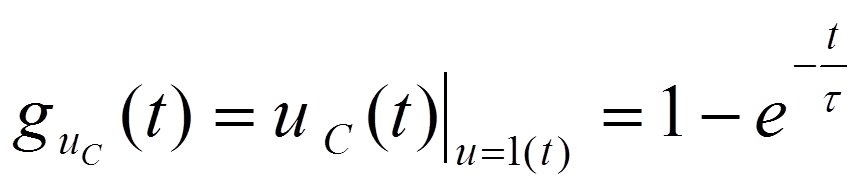 - переходная хар-ка по напряжению
- переходная хар-ка по напряжению
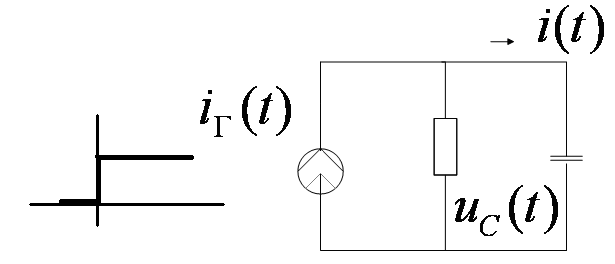
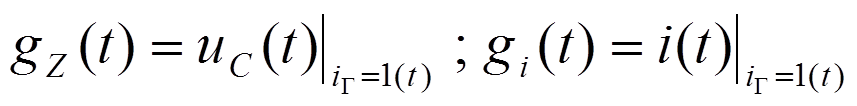
???????????
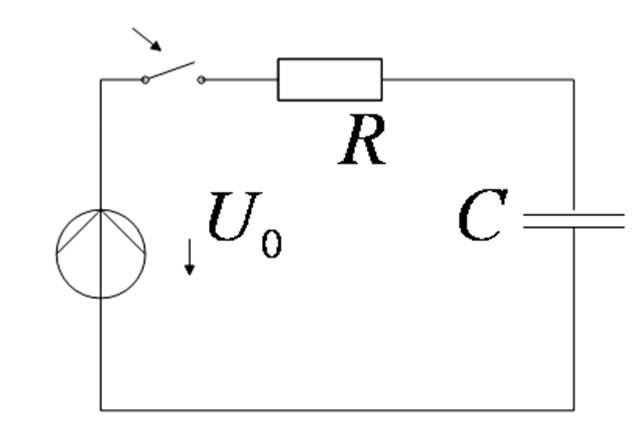
Расчет переходной хар-ки:
а) классический метод
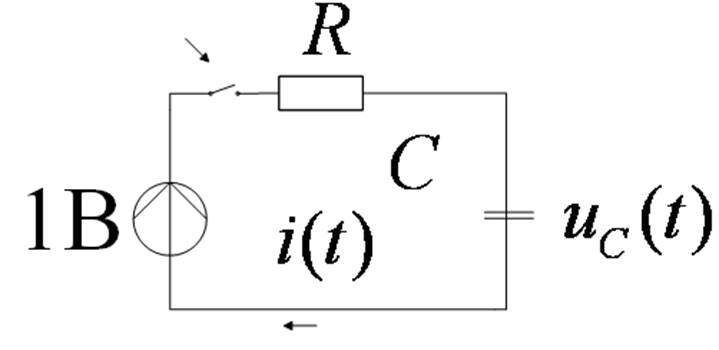
б) операторный метод
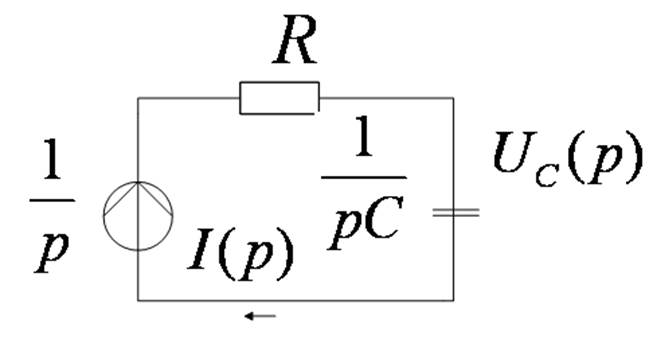

9.2. Интеграл Дюамеля
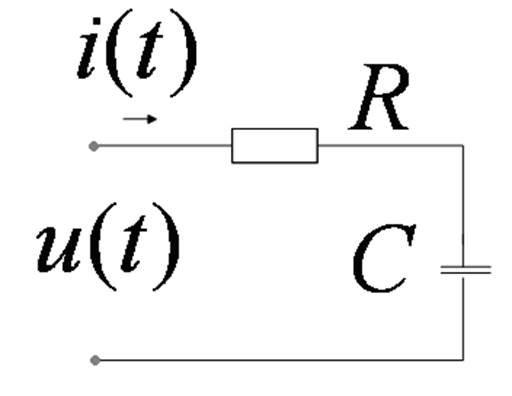
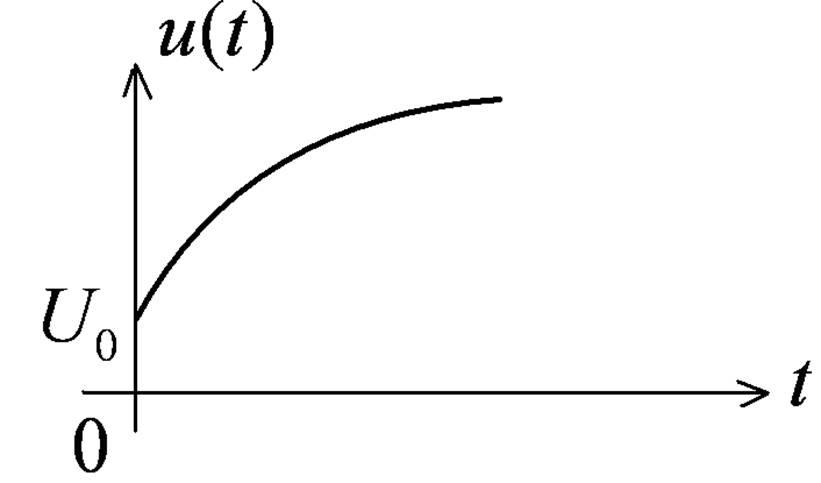
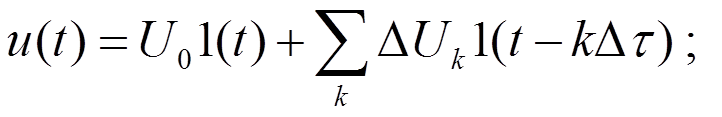
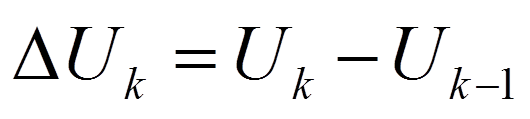
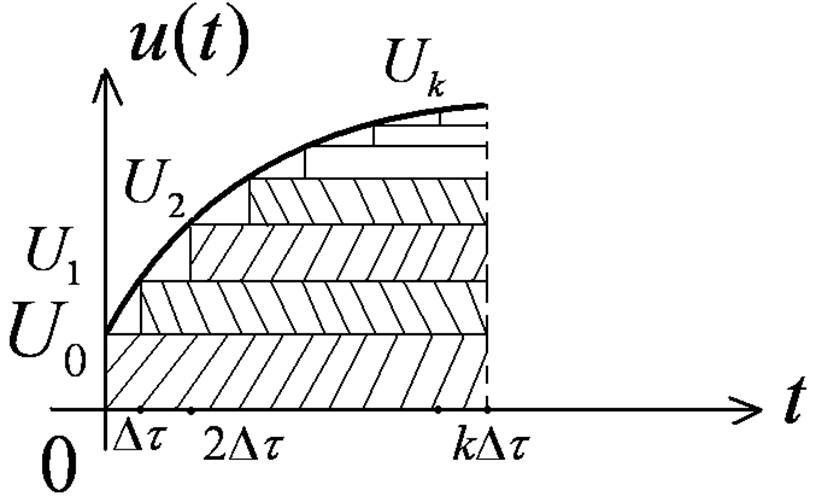
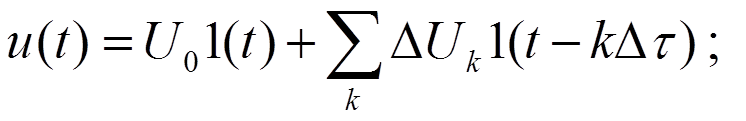
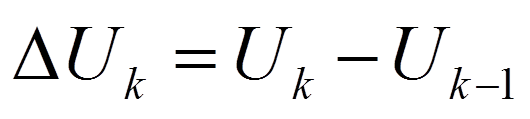
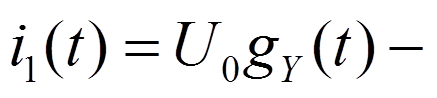 реакция на 1-ый
скачок
реакция на 1-ый
скачок
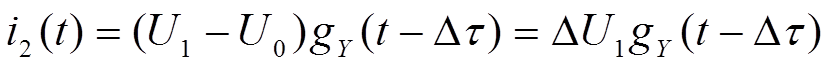 -реакция на 2-ой скачок
-реакция на 2-ой скачок
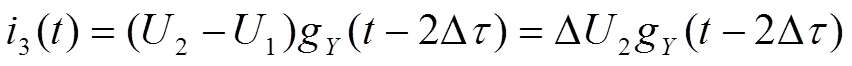 -реакция на 3-ий скачок
-реакция на 3-ий скачок
и т.д.
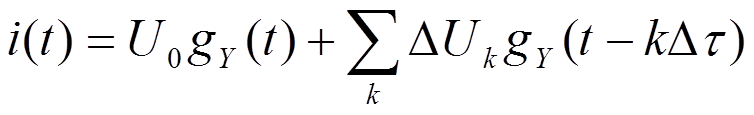
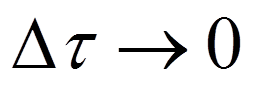
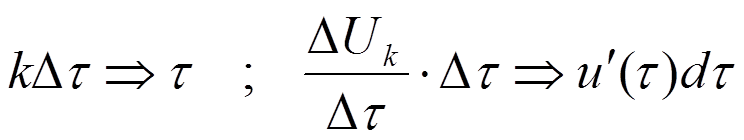

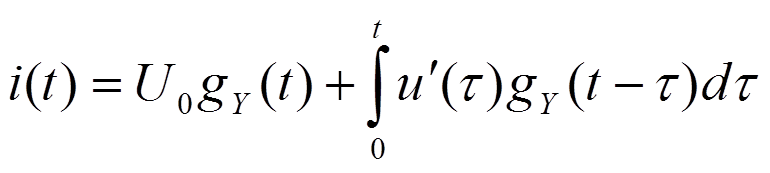
- это 1-ая форма интеграла Дюамеля

- 2-ая форма
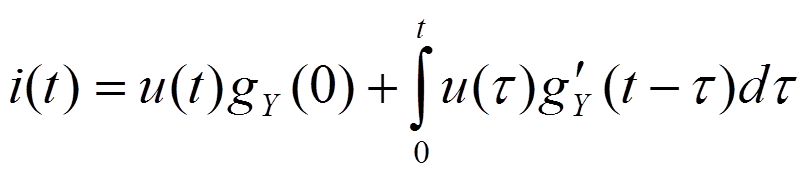 - 3-я форма
- 3-я форма
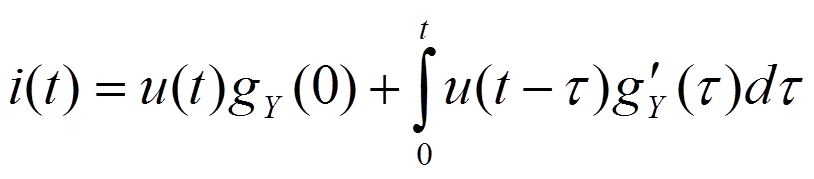 - 4-ая форма
- 4-ая форма

9.3. Расчет цепей с помощью интеграла Дюамеля
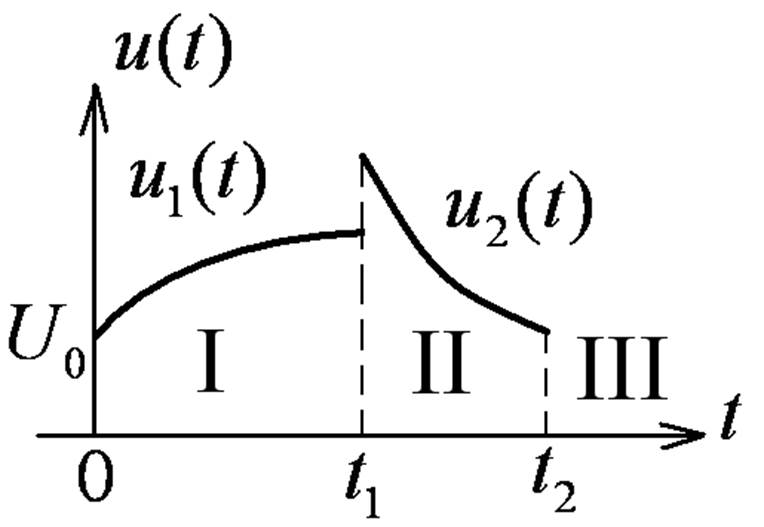
Интервал 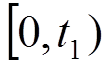
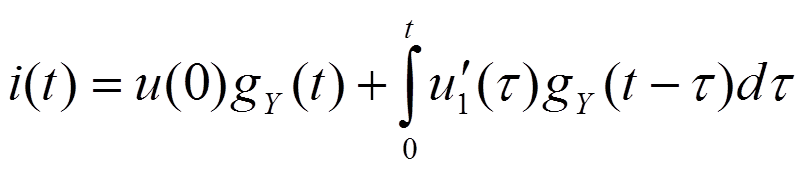 Интервал
Интервал 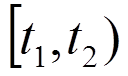
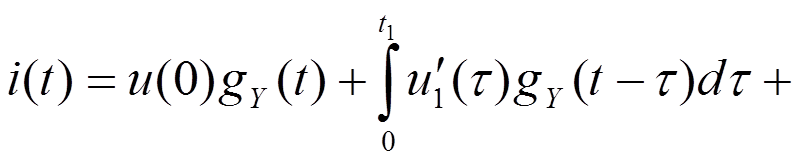
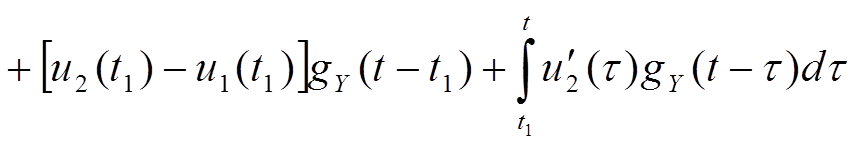 Интервал
Интервал 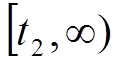
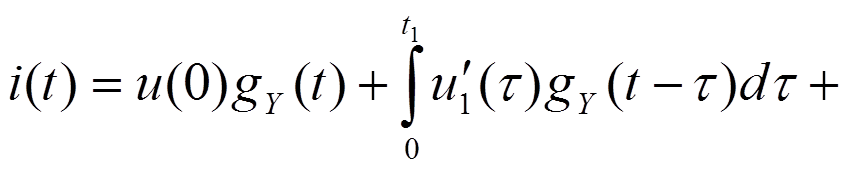
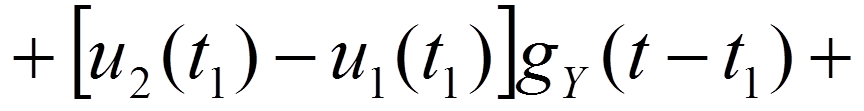
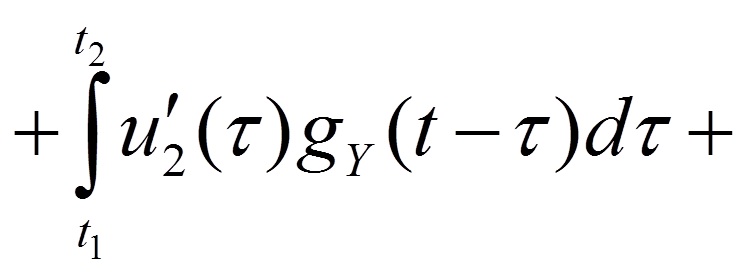
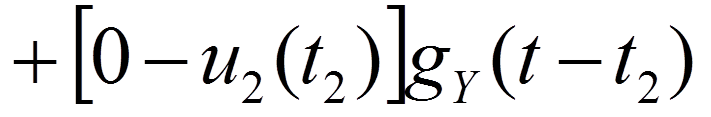
Пример
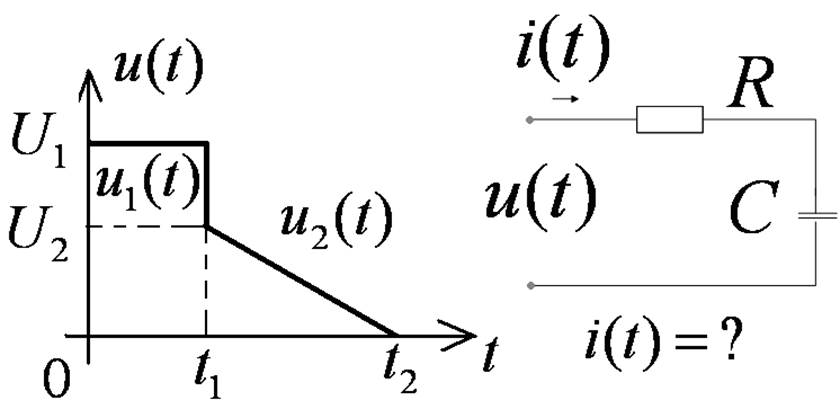
1) 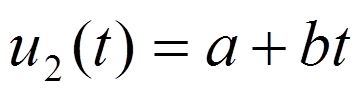
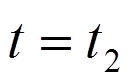 :
:
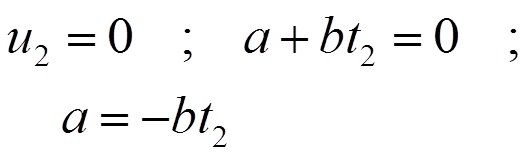
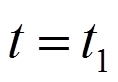 :
:
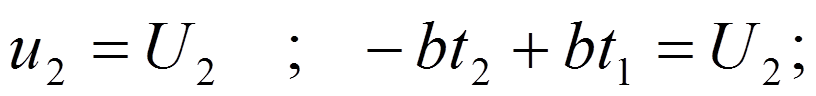
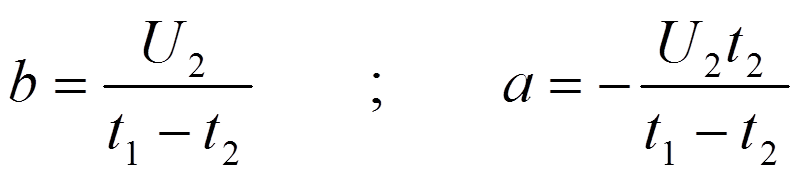
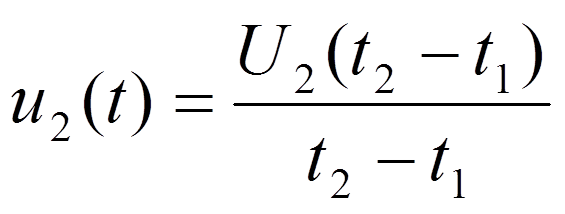
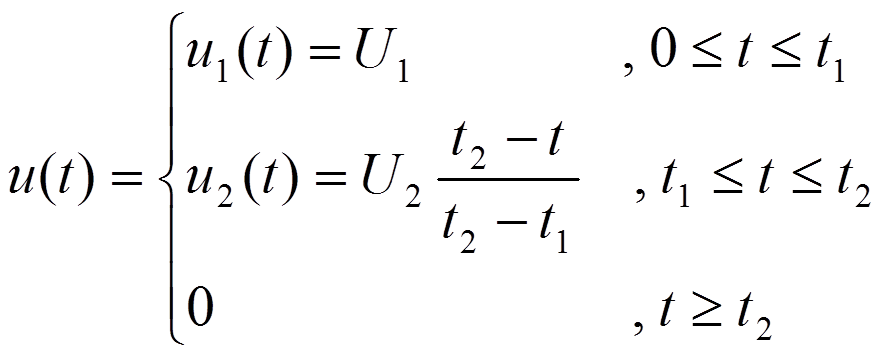 2) Переходные характеристики RC цепи
2) Переходные характеристики RC цепи
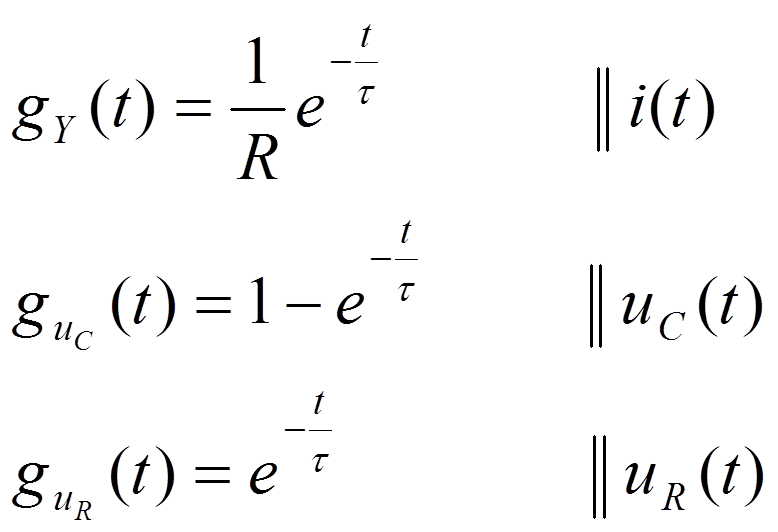
3)
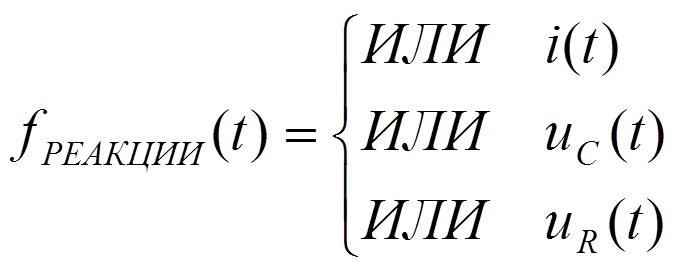
Интервал 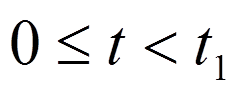

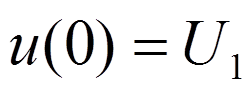
Интервал 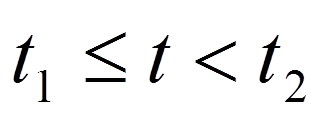
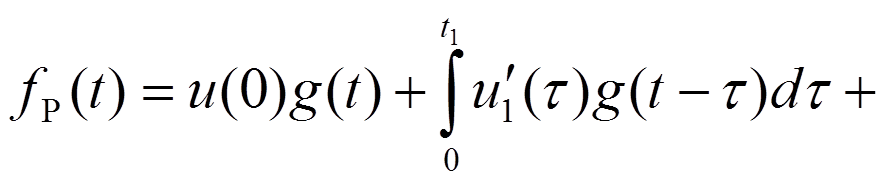
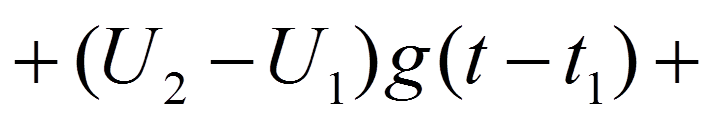
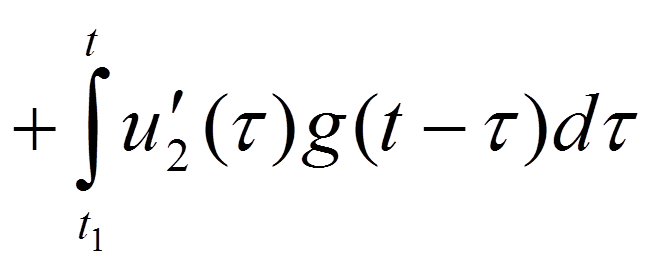
Интервал 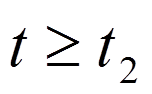
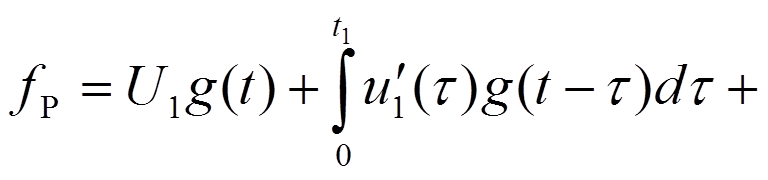
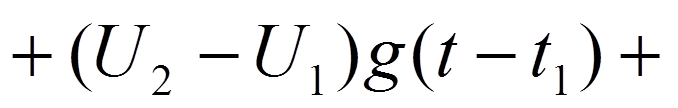
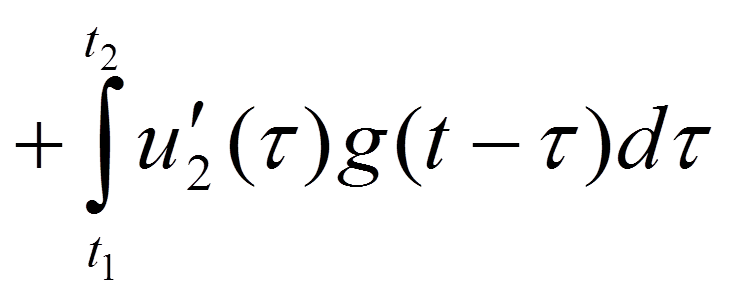
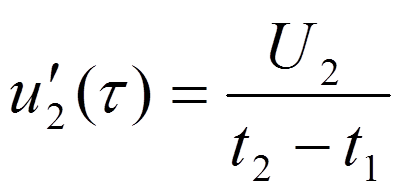
 9.4. Импульсные характеристики цепи
9.4. Импульсные характеристики цепи
δ- импульс
(δ-функция, функция Дирака)
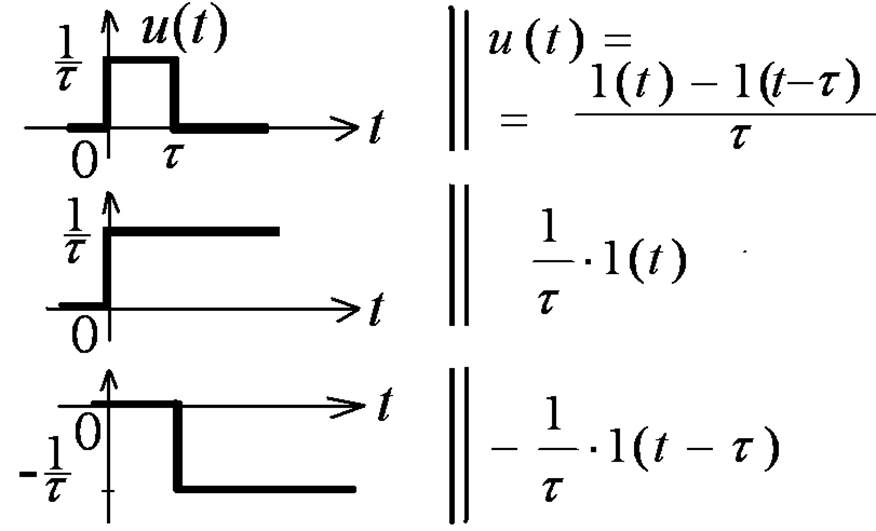
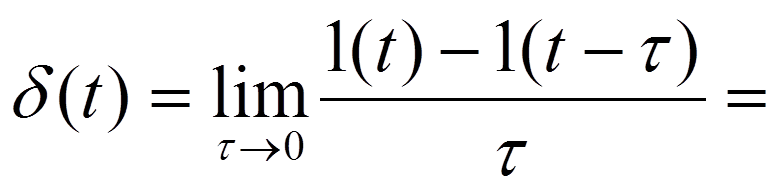
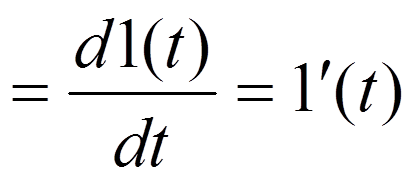
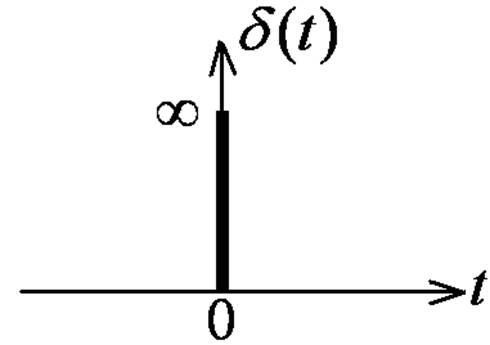
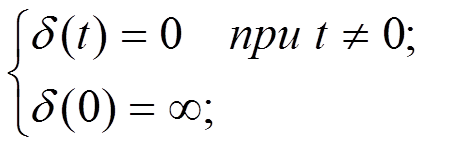
Площадь δ-импульса
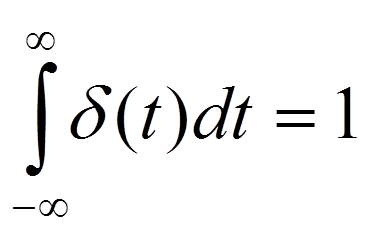
Фильтрующее свойство
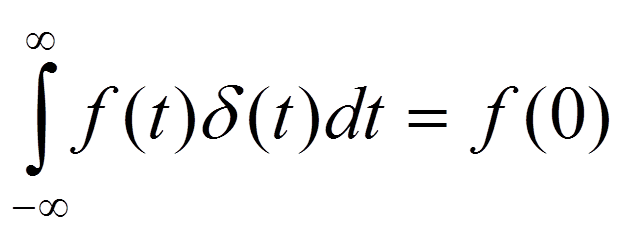
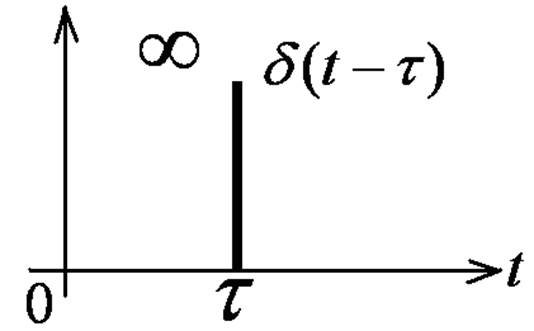
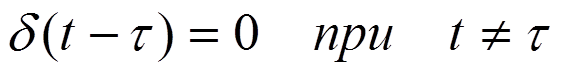
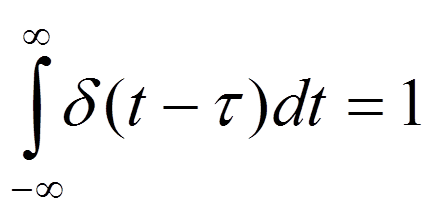
![]()
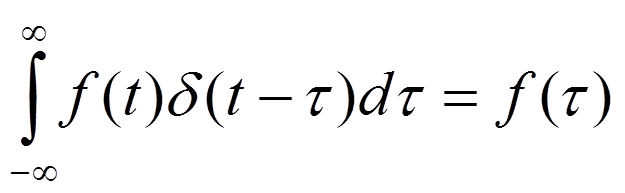
Изображение δ-функции
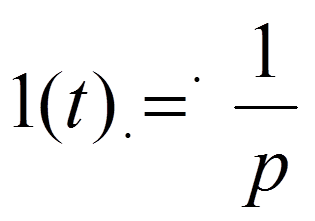
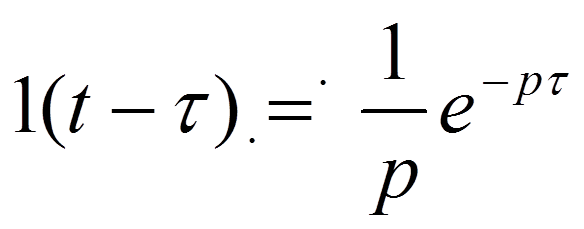
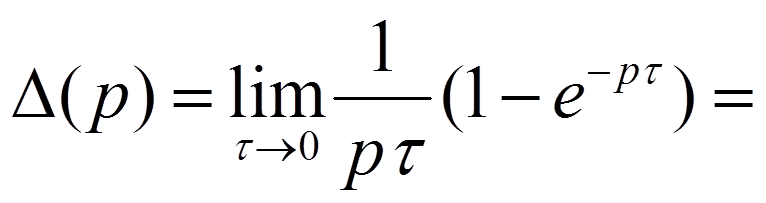
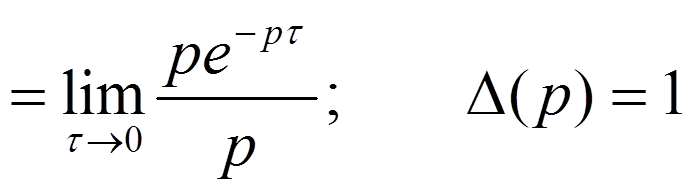

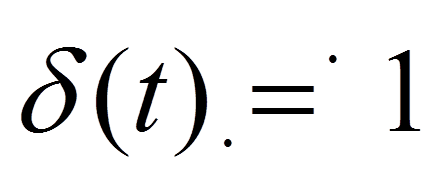
Импульсная
характеристика – реакция цепи
на воздействие в виде δ-импульса 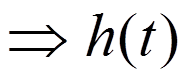 .
.
Связь с переходной характеристикой.
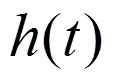 - реакция на
- реакция на 
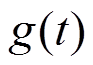 - реакция на
- реакция на 
Так как
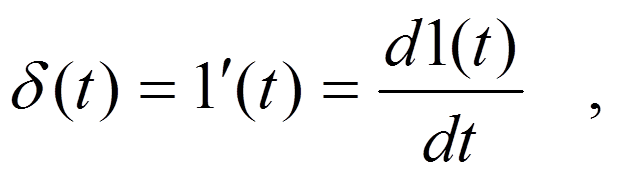
 то
то
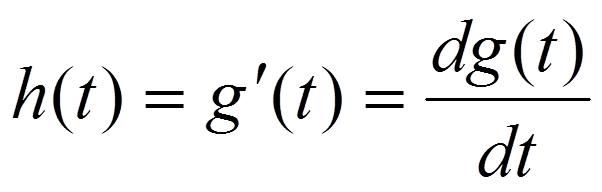
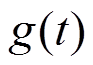 - непрерывная функция
- непрерывная функция
Если
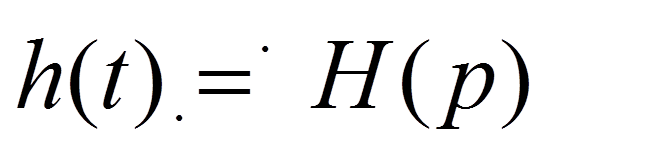
И
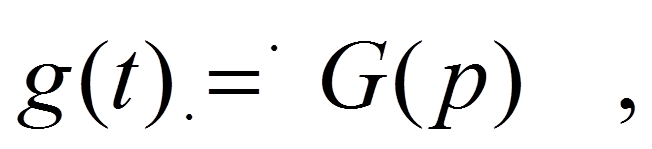
 то
то
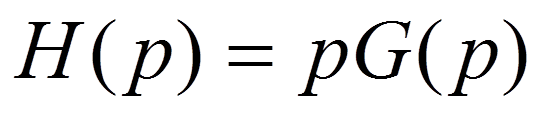
Пусть 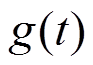 имеет разрыв (скачок):
имеет разрыв (скачок):
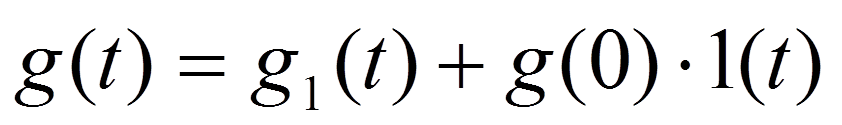
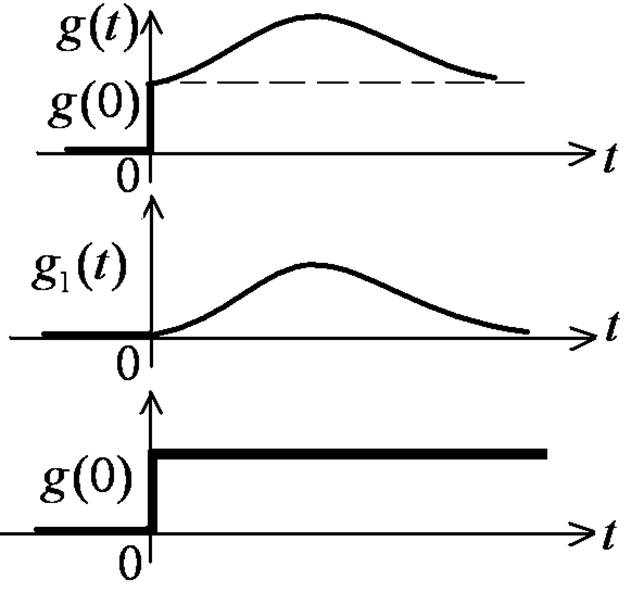
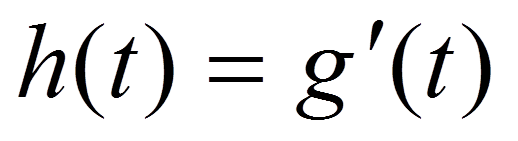
или
![]()
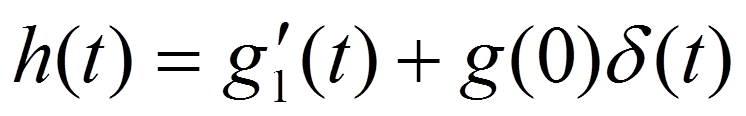 так как
так как 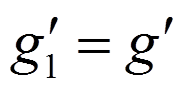 ,то
,то
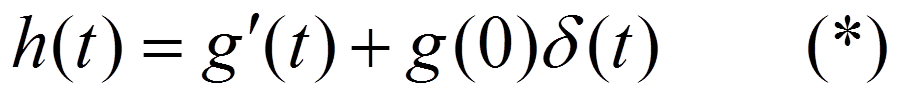
Определение 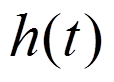 :
:
1.
Находят 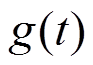 и путём дифференцирования получают
и путём дифференцирования получают 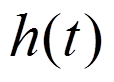 .
.
2.
Находят операторным
методом 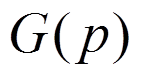 , переходят к
, переходят к 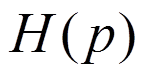 и
отыскивают оригинал
и
отыскивают оригинал 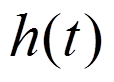 .
.
3.
Находят непосредственно по
операторной схеме 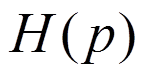 , а затем
, а затем 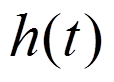 .
.
ПРИМЕР
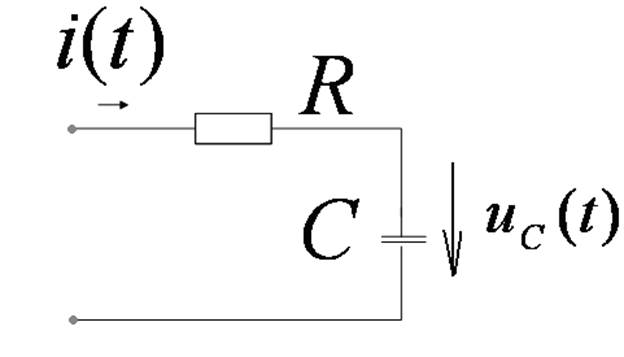
1. 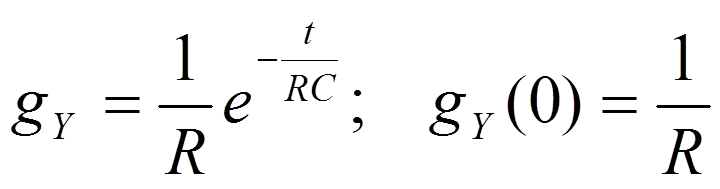
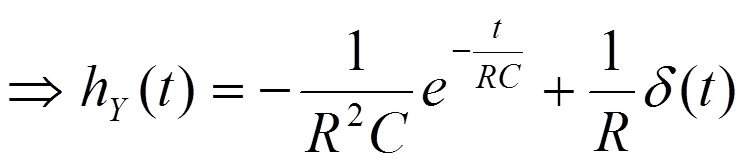
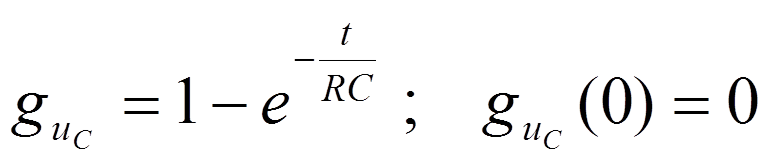
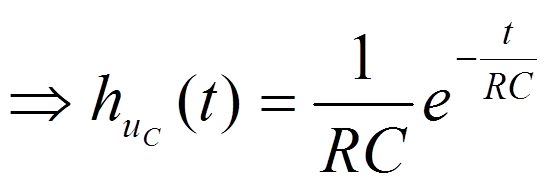
2.
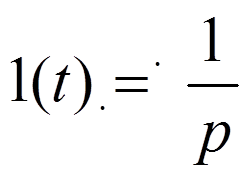
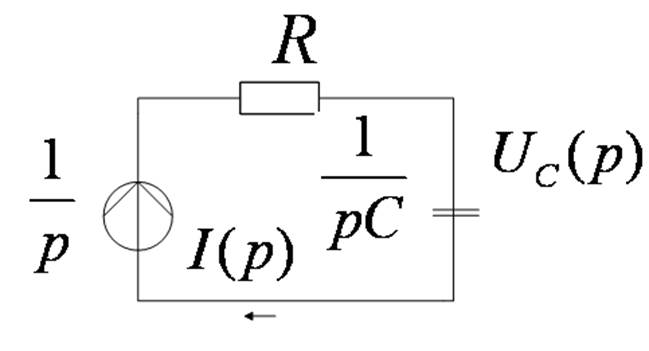
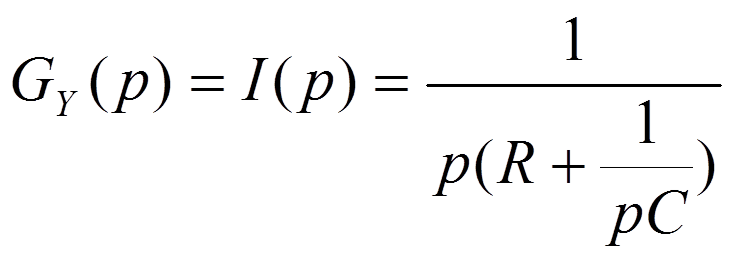
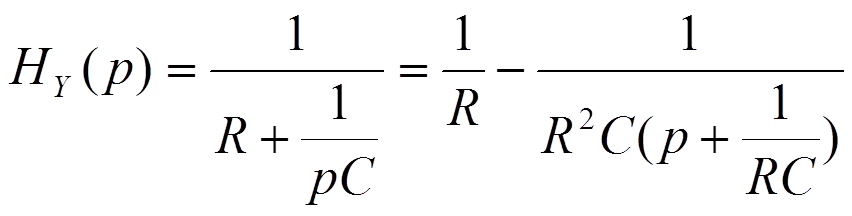
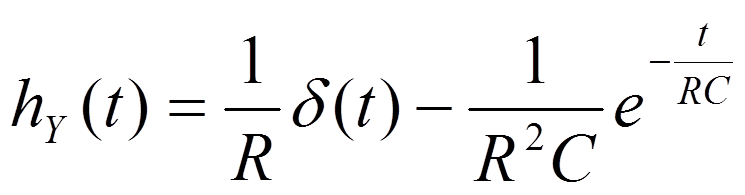
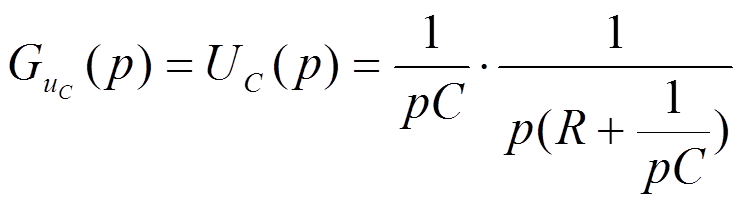
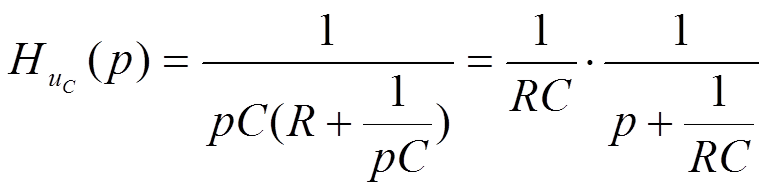
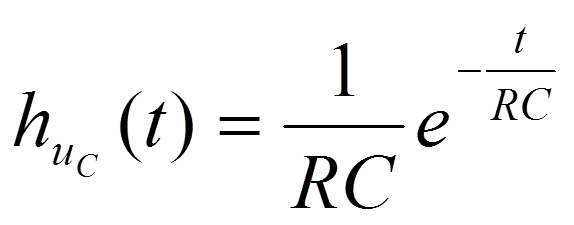
3.
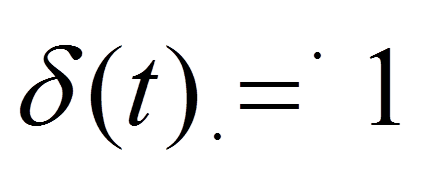
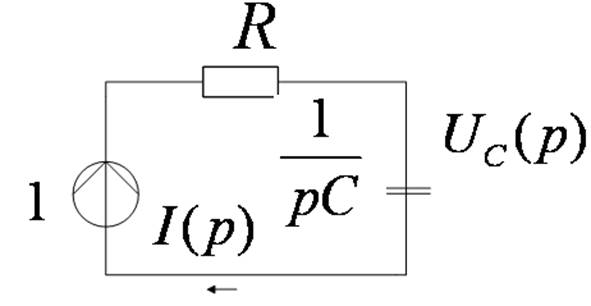
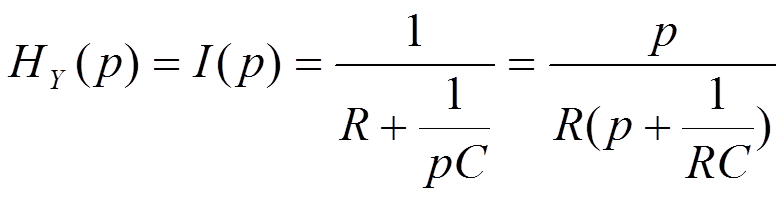
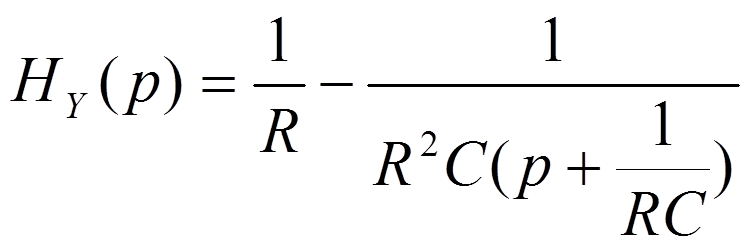
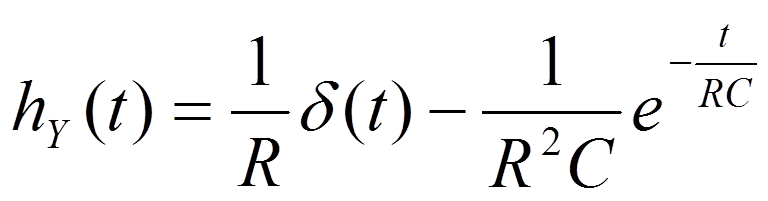
![]()
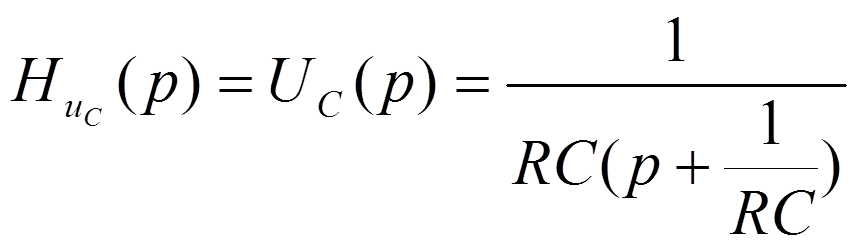
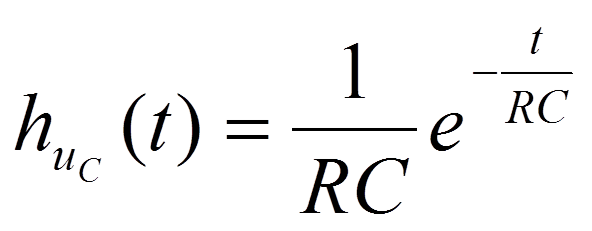
![]()
9.5. Интеграл наложения (интеграл свёртки)

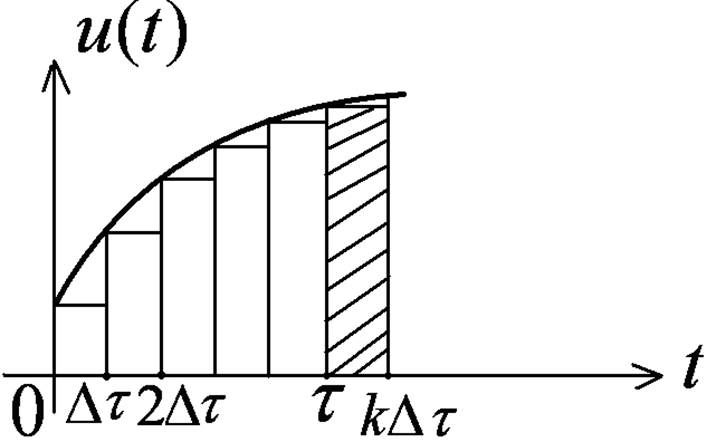
Площадь импульса
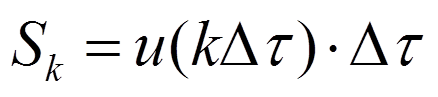
Площадь δ-импульса
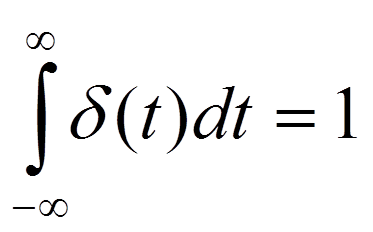
Реакция на δ-импульс 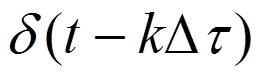 равна
равна  .
.
Реакция на k-ый импульс будет в 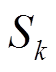 раз больше:
раз больше:
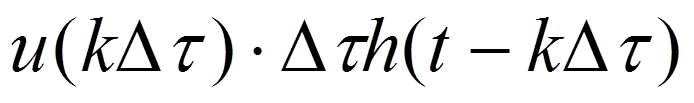
![]()
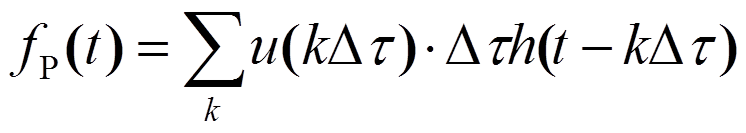 при
при 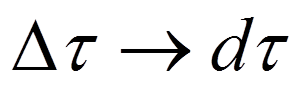
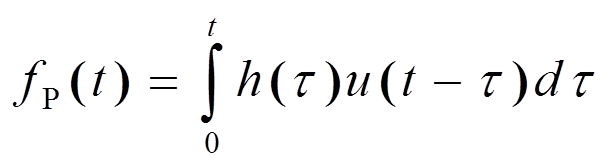
- вторая форма интеграла.
![]() 9.6. Интегрирующие и дифференцирующие цепи
9.6. Интегрирующие и дифференцирующие цепи
Интегрирующие цепи- это цепи, у которых реакция пропорциональна интегралу от приложенного напряжения.
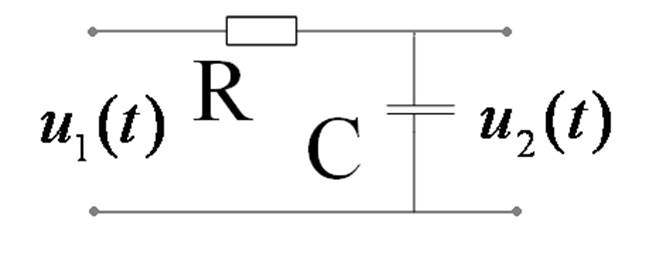
Интеграл наложения:
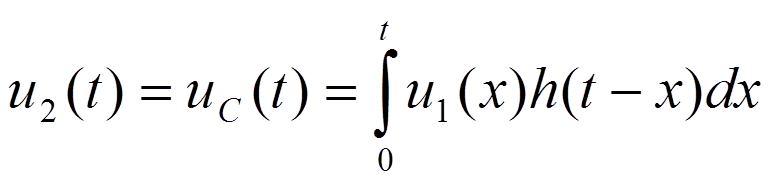
где
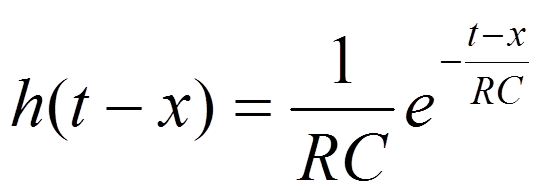
- импульсная характеристика
RC=τ – постоянная времени
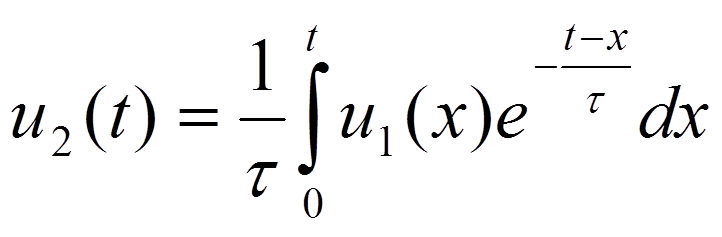 при t‹‹τ (или τω‹‹1)
при t‹‹τ (или τω‹‹1)
 ряд можно ограничить первым членом.
ряд можно ограничить первым членом.
Тогда
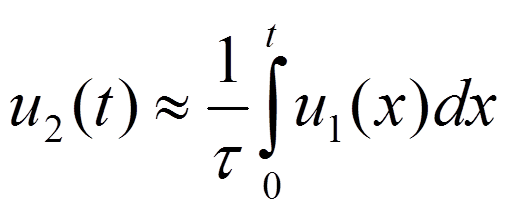
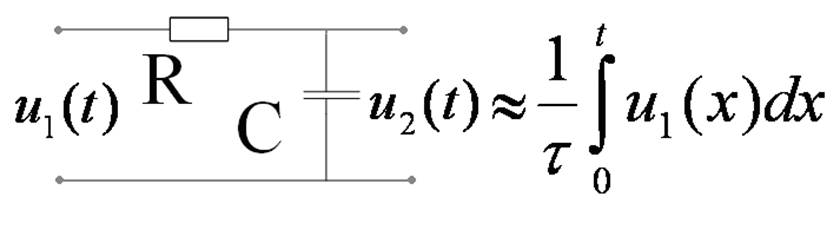
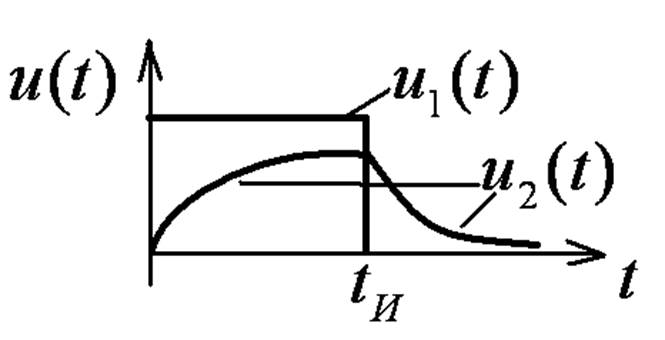
Это RC-интегрирующая цепь.
Для импульсных воздействий длительностью 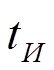 условие
качественного интегрирования:
условие
качественного интегрирования:
τ››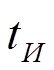
RL-интегрирующая цепь
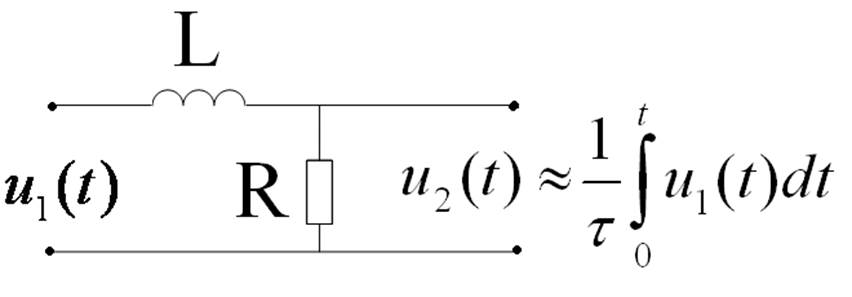
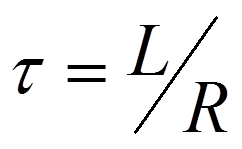
Условия качественного интегрирования: τ››t; τω››1; τ››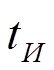 .
.
RC и LR-дифференцирующие цепи
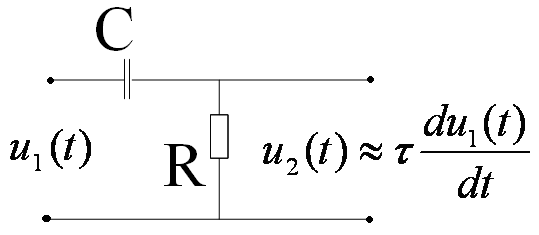
τ=RC
Дифференцирующие цепи - это цепи, у которых реакция пропорциональна производной от приложенного напряжения.
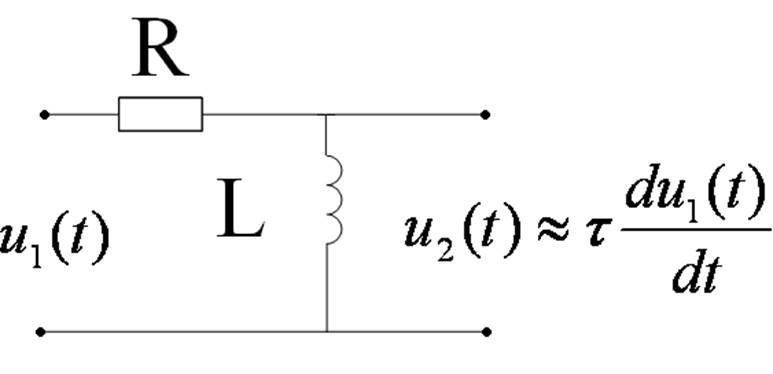
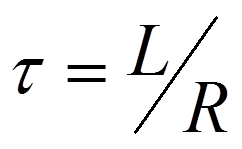
Условия качественного дифференцирования:τ‹‹t; τω‹‹1; τ‹‹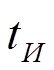
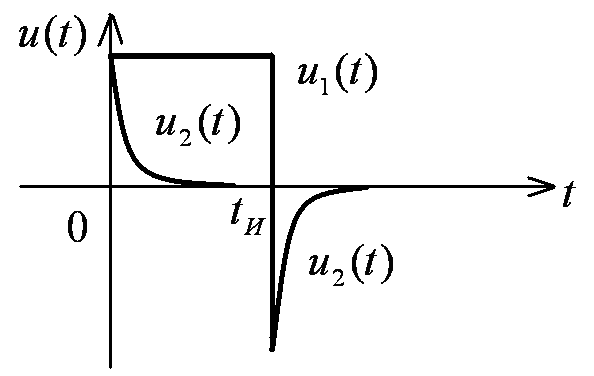
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.