



















Введение
Основные понятия и законы ОТЭЦ Электрическая цепь – совокупность устройств, предназначенных для прохождения электрического тока, и описываемых с помощью понятий тока и напряжения. Электрическая цепь состоит из источников и приемников электрической энергии. Источники электрической энергии – устройства, создающие токи и напряжения. Приемники электрической энергии – устройства, потребляющие (запасающие) электрическую энергию, или преобразующие электрическую энергию в другие виды энергии. Физические элементы электрических цепей – резисторы, катушки индуктивности, транзисторы, электрические лампы и другие компоненты электроники. Свойства физических реальных элементов электрической цепи, и происходящие в них физические явления, описываются с помощью моделей, поэтому реальная электрическая цепь заменяется некоторой идеализированной моделью, состоящей из взаимосвязанных и идеализированных элементов. Система элементов, описывающая модель электрической цепи, называется математической моделью электрической цепи. Электрический ток – различают токи проводимости, ток переноса, ток смещения. Ток проводимости – упорядоченное движение зарядов в среде под действием электрического поля. Ток переноса – упорядоченное движение зарядов в вакууме под действием электрического поля. Ток смещения – изменение во времени электрического поля.
Лекция 1
Источники электрической энергии
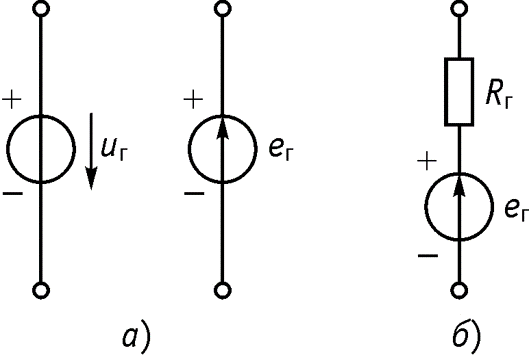
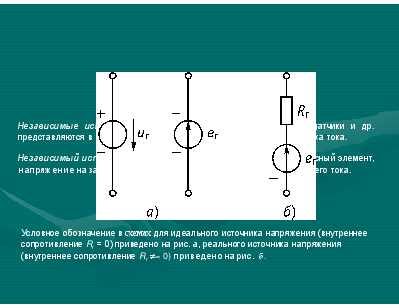
Независимые источники – аккумуляторы, термоэлементы, пьезодатчики и др. представляются в виде двух моделей: источника напряжения и источника тока. Независимый источник напряжения – идеализированный двухполюсный элемент, напряжение на зажимах которого не зависит от протекающего через него тока.
![]()
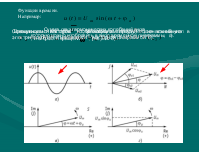
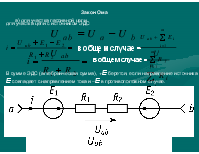
Условное обозначение в схемах для идеального источника напряжения (внутреннее сопротивление Rг = 0) приведено на рис. а, реального источника напряжения (внутреннее сопротивление Rг = 0) приведено на рис. б.
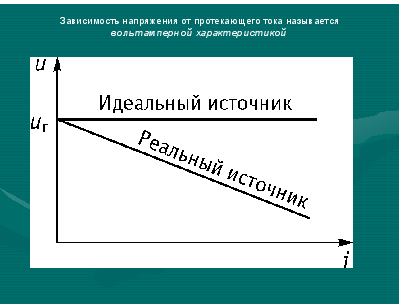
Зависимость напряжения от протекающего тока называется вольтамперной характеристикой
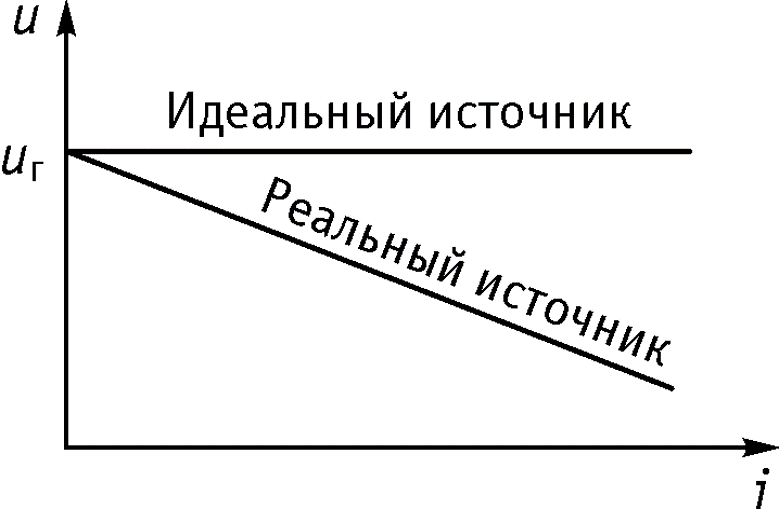
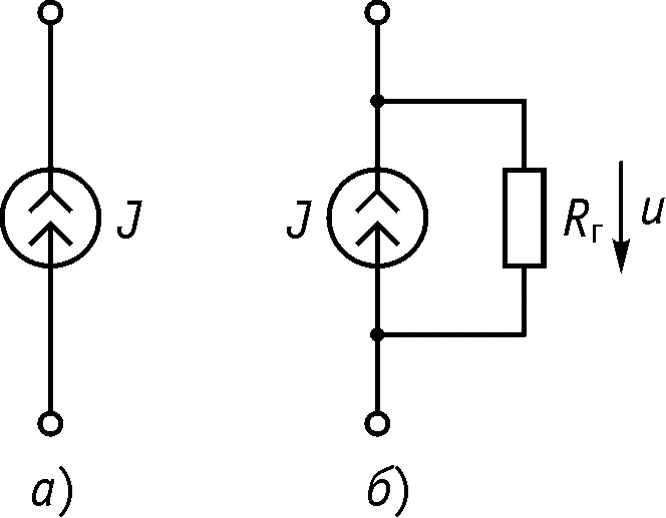
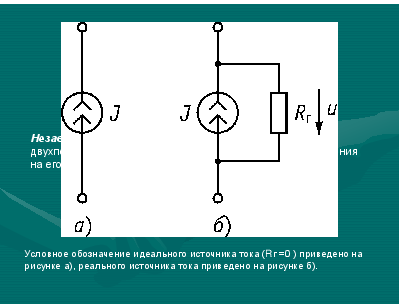
Независимый источник тока – идеализированный двухполюсный элемент, ток которого не зависит от напряжения на его зажимах.
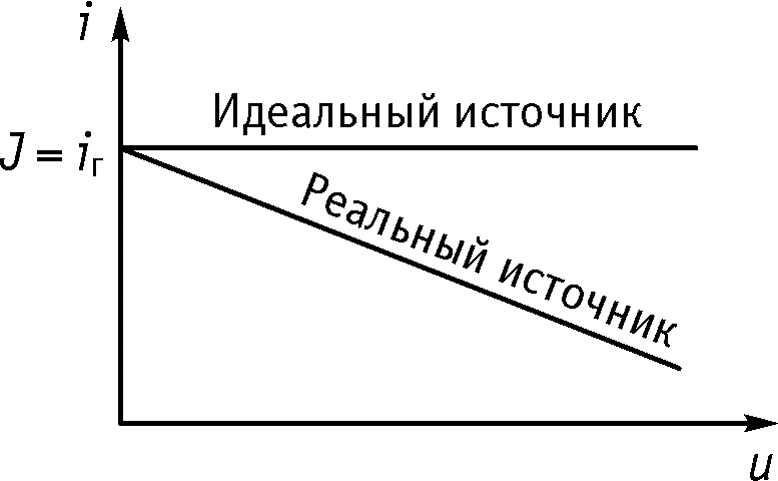
Условное обозначение идеального источника тока (Rг =0 ) приведено на рисунке а), реального источника тока приведено на рисунке б).
Зависимость тока от напряжения называется вольтамперной характеристикой источника тока.
Синусоидальный ток и напряжение. амплитуда, фаза, частота
Синусоидальный ток и напряжение по сути представляют собой гармонические колебания Гармоническое колебание – движение или изменение состояния материальных тел или материи (W, q, I, U, P) вокруг некоторого среднего значения по закону простейшей периодической функции вида
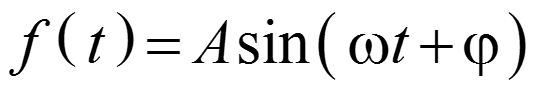
Гармоническое колебание характеризуется: амплитудой, начальной фазой, текущей фазой, угловой частотой, циклической частотой, средним значением за период, средним значением за полупериод, действующим значением.
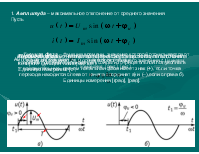
1. Амплитуда – максимальное отклонение от среднего значения Пусть
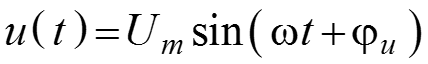
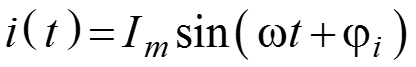
Амплитуда напряжения показана на рисунке.
Текущая фаза – функция времени, значение которой отсчитывается от начала координат t = 0 до некоторого текущего значения t. Единицы измерения: [град], [рад].
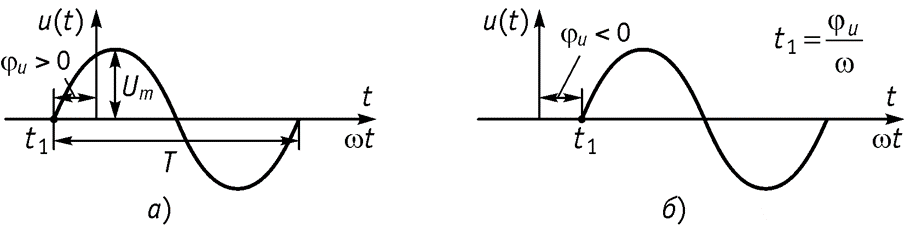
Начальная фаза – значение смещения синусоиды относительно начала координат до точки перехода синусоиды из отрицательной полуволны в положительную, причем начальная фаза имеет знак (+), если точка перехода находится слева от начала координат а) и (–),если справа б). Единицы измерения [град], [рад].
Период колебания – наименьший промежуток времени, по истечении которого функции повторяются. Единицы измерения: [c]
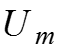
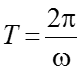
![]()
.
![]()
![]()
![]()
![]()
Угловая частота – скорость изменения текущей фазы.
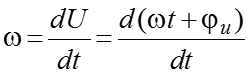
[рад/c].
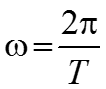
![]()
Циклическая частота
![]()
– величина обратная периоду
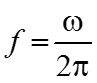
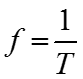
; [Гц] , [1/c]
Мгновенное значение – значение функции в произвольный момент времени
.
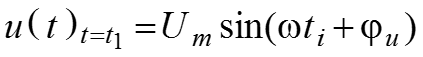
.
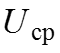
Среднее значение за период
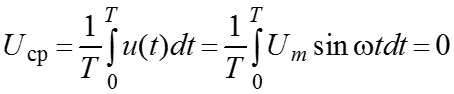
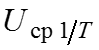
Среднее значение за полпериода
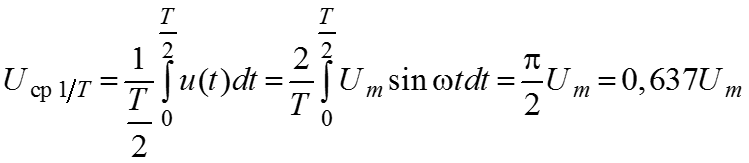
Действующее значение за период
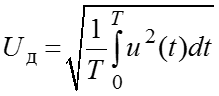
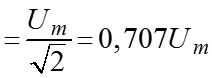
Замечание: все соотношения, полученные для напряжений, используя принцип дуальности, можно перевести на ток.
.
Способы представления гармонических колебаний
Функции времени. Например:
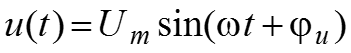
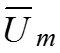
![]()
Сумма двух гармонических колебаний вида
Вращающимся вектором
, имеющим амплитуду
, начальный угол
Совокупность векторов, изображающих гармоническое колебание в электрической цепи называется – векторной диаграммой б).
, которую можно изобразить в виде временной диаграммы, а).
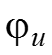
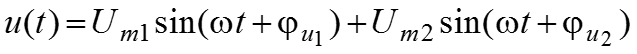
, и скорость вращения
![]()
, рисунок б).

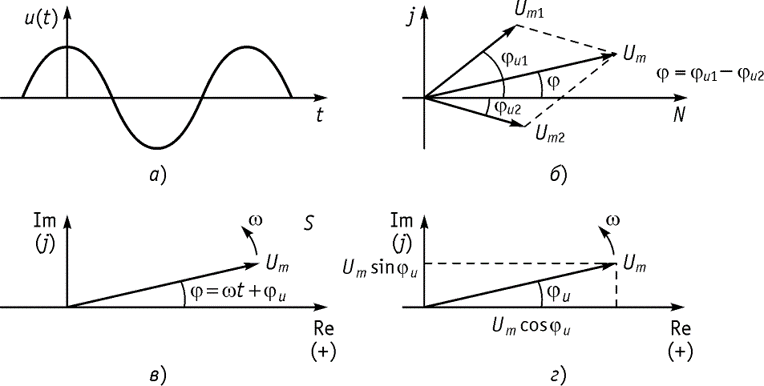

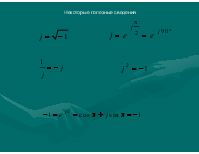
Представление гармонических колебаний комплексными числами
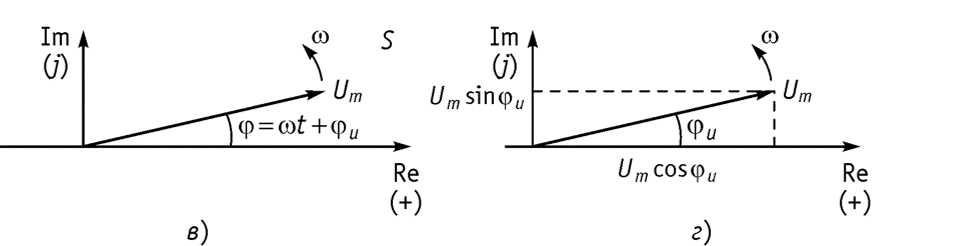
Представление гармонических колебаний комплексными числами может быть в следующих формах:
Изобразить комплексную величину можно в виде векторов на комплексной
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.