Разработка и применение алгоритма цифровой обработки сигналов при передаче дискретных сообщений по частотно-ограниченному каналу связи, страница 3

В математической форме условие Найквиста можно записать так:

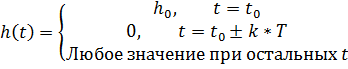
Необходимо также заметить, что вследствие прямоугольной формы передаточной характеристики и бесконечной длины соответствующего импульса подобные идеальные фильтры нереализуемы, их можно реализовать лишь приближенно.

1.3 Второе условие Найквиста

Первое условие Найквиста накладывает жесткие требования на качество синхронизации, так как для предотвращения появления МСИ детектор должен производить выборку точно в соответствующие моменты времени, кратные T. Функция вида sinc(t/T) имеет хвосты достаточно больших амплитуд около главного лепестка каждого импульса, поэтому в случае ошибки синхронизации (т.е. когда выборка производится в моменты времени не кратные T) появляется межсимвольная интерференция. Поэтому на практике используются импульсы другой формы, импульсная характеристика которых удовлетворяет условию:

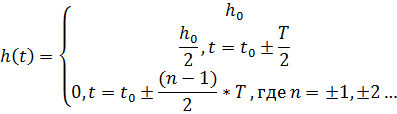
У импульсной реакции такого вида в середине интервала между временем взятия отсчетов наложение сигнала равно 0 либо ±1.

Этим условиям удовлетворяет передаточная функция типа «приподнятый косинус»

Передаточная характеристика:

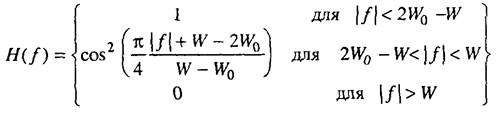
Здесь W – максимальная ширина полосы; W₀ = 1/2T – минимальная ширина полосы по Найквисту и ширина полосы по уровню  –6 дБ (или точка половинной амплитуды) для косинусоидального спектра. Коэффициент сглаживания r характеризует крутизну фронта характеристики фильтра и определяется формулой:

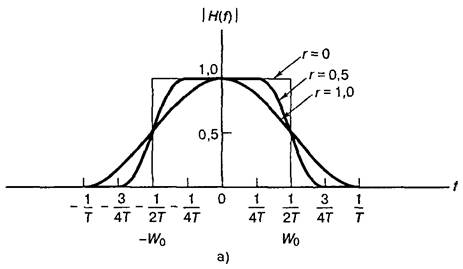
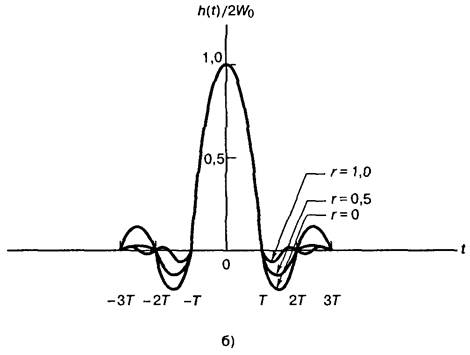
Рисунок 1.4 – Характеристики фильтров типа приподнятого косинуса для разных значений r: а) передаточная функция системы; б) импульсный отклик системы

Передаточная функция, имеющая вид приподнятого косинуса – это общесистемная функция, описывающая «полный проход» сообщения, отправленного передатчиком (в виде импульса) через канал и принимающий фильтр. Фильтрация в приемнике осуществляется частью общей передаточной функции, тогда как подавление межсимвольной интерференции, обеспечивает передаточная функция, имеющая вид приподнятого косинуса. Как следствие сказанного, принимающий и формирующий фильтр часто согласовываются так, чтобы передаточная функция каждого имела вид квадратного корня из приподнятого косинуса. Подавление межсимвольной интерференции, внесенной каналом, обеспечивает произведение этих двух функций, которое дает общую передаточную функцию системы, имеющую вид приподнятого косинуса. Если же для уменьшения последствий привнесенной каналом МСИ вводится отдельный выравнивающий фильтр (корректор), принимающий и выравнивающий фильтры могут совместно настраиваться так, чтобы компенсировать искажение, вызванное как передатчиком, так и каналом; при этом общая передаточная функция системы характеризуется нулевой межсимвольной интерференцией.

1.4 Расчет формирующего фильтра

Рассчитаем формирующий фильтр с характеристикой типа корень из приподнятого косинуса. Импульсная реакция фильтра:

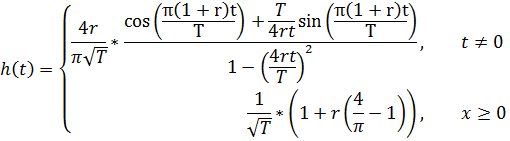
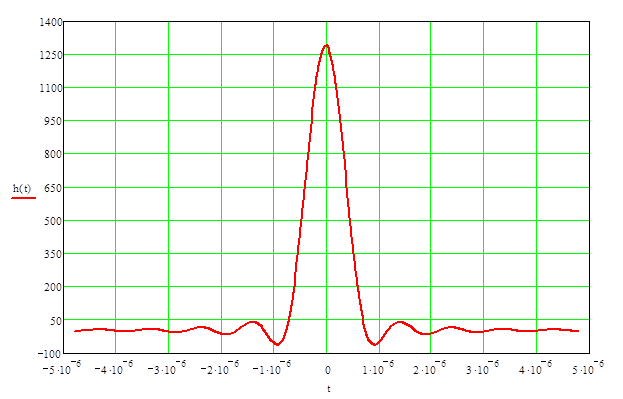
Рисунок 1.5 – Импульсная реакция фильтра корень из приподнятого косинуса

Зададим длительность тактового интервала T = 1.2 мкс и интервал между отсчетами Δt = 0.4 мкс; коэффициент сглаживания r = 0.4+0.1*11 = 1.5

Найдем отсчеты импульсной реакции формирующего фильтра на интервале [–4T; 4T]:

h[n] = [ -3.032; 3.044; -2.374; -0.3; 3.048; -8.062; 12.192; -14.371; 16.833; 8.302;  -32.951; 648.58; 1287; 648.58; -32.951; 8.302; 16.833; -14.371; 12.192; -8.062; 3.048; -0.3; -2.374; 3.044; -3.032 ]

Рассчитаем при помощи встроенной функции MATLAB АЧХ и ФЧХ формирующего фильтра.

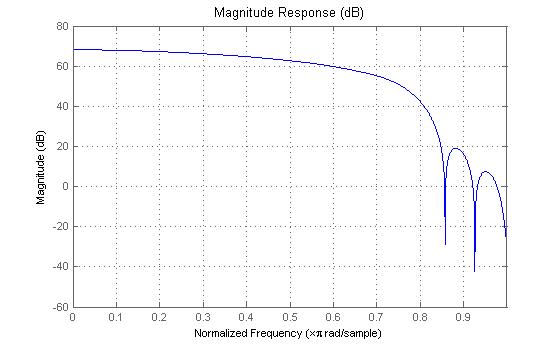
Рисунок 1.6 – АЧХ формирующего фильтра

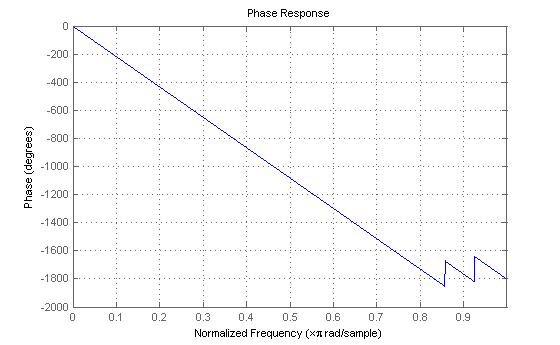
Рисунок 1.7 – ФЧХ формирующего фильтра

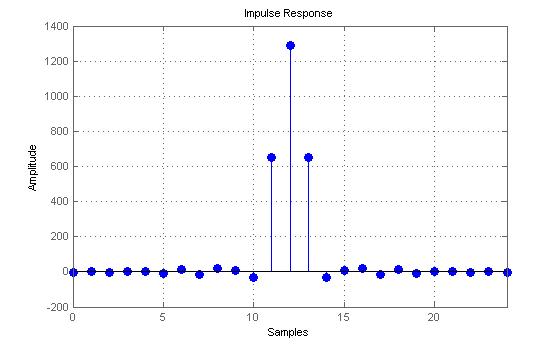
Рисунок 1.8 – Отсчеты импульсной реакции формирующего фильтра

2 Адаптивная коррекция

2.1 Алгоритмы коррекции

При увеличении скорости передачи сигналов полоса частот расширяется, следовательно, уменьшается длительность тактового интервала, а это, как было показано выше, ведет к увеличению МСИ.

Для борьбы с межсимвольной интерференцией используются выравнивающие фильтры (корректоры). ЧХ выравнивающего фильтра выбирается таким образом, чтобы скомпенсировать искажения сигнала, внесенные как формирующим фильтром, так и каналом связи. При этом добиваются того, чтобы общесистемная передаточная функция H(ω) имела форму, обеспечивающую минимальную МСИ, например, приподнятый косинус.