Построить идеальный канал, описываемый приведенным выше уравнением нереально. Проблема заключается в том, что в данном уравнении предполагается бесконечная ширина полосы, в которой АЧХ имеет заданную величину, а так как реализовать канал с бесконечной полосой часто невозможно, реальные каналы связи являются частотно ограниченными, т.е. неидеальными. В качестве приближения к идеальному каналу можно использовать усеченный канал, без искажения пропускающий все гармоники в интервале частот от f1 до f2 (случай идеального фильтра). В результате прохождения сигнала по такому каналу его форма может довольно сильно исказиться из-за подавления части спектра. В качестве примера можно рассмотреть прохождение прямоугольного импульса по частотно ограниченному каналу связи (случай ФНЧ).
Рисунок 1.1 – Искажение формы прямоугольного импульса
Как видно из рисунка, при прохождении прямоугольного импульса через частотно ограниченный канал связи его бесконечный спектр ограничивается, что приводит к изменению формы – вместо гладкой вершины появляются пульсации, а сам импульс как бы растягивается во времени. Это явление может приводить к возникновению межсимвольной интерференции (МСИ).
Для объяснения появления МСИ рассмотрим типичную систему цифровой связи. В системе – передатчике, приемнике и канале используется множество фильтров. На рисунке приведена модель системы, объединяющая все эффекты фильтрации в одну общесистемную передаточную функцию:
![]()
где Hформ(ω) – ЧХ формирующего (передающего) фильтра
Hк(ω) – ЧХ канала
Hпр(ω) – ЧХ принимающего фильтра
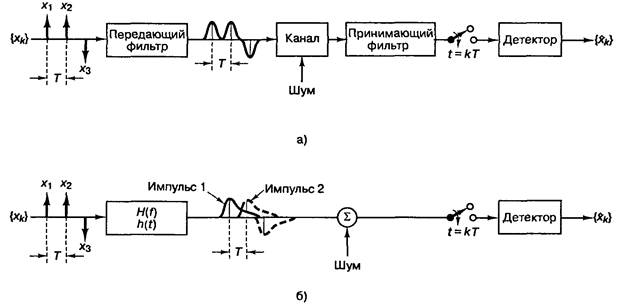
Рисунок 1.2 – Межсимвольная интерференция в процессе детектирования:
а) типичная цифровая система; б) эквивалентная модель
В бинарной системе, использующей какую-нибудь распространенную кодировку, например NRZ, детектор принимает решение о значении символа путем сравнения значения отсчета сигнала, взятого в момент времени, кратный Т, со значением порога (на рисунке значение порога – 0). При прохождении импульсов через частотно ограниченный канал спектр импульсов ограничивается, в результате чего импульсы растягиваются во времени. Хвост импульса размывается на соседний интервал передачи и прибавляется к значению отсчета сигнала, мешая таким образом процессу детектирования и повышая вероятность ошибки. Этот процесс получил название межсимвольной интерференции.
Для борьбы с МСИ можно увеличить продолжительность тактового интервала, чтобы хвосты импульсов не накладывались друг на друга, однако этот метод неприемлем, так как скорость передачи информации обратно пропорциональна продолжительности тактового интервала:
![]()
Следовательно, при увеличении T снизится скорость передачи R, что малоприемлемо.
Исследованием методов борьбы с межсимвольной интерференцией занимался Найквист
1.2 Первое условие Найквиста
Найквист доказал, что минимальная ширина полосы системы, требуемая для детектирования Rs символов в секунду без МСИ равна Rs/2 Гц. Это возможно, если передаточная функция системы H(f) имеет прямоугольную форму, односторонняя ширина полосы которой равна 1/2T. Импульсная реакция данной системы h(t), вычисляемая при помощи обратного преобразования Фурье имеет вид h(t) = sinc(t/T) = sin(t/T)/(t/T)
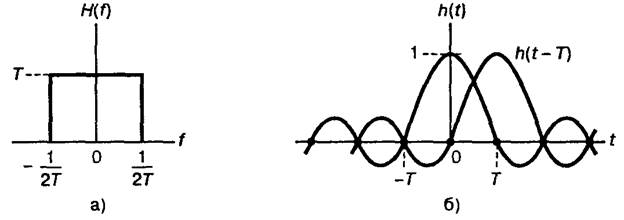
Рисунок 1.3 – Канал Найквиста для нулевой межсимвольной интерференции а) прямоугольная передаточная функция системы H(f); б) принятые импульсы h(t) и h(t – T)
Найквист установил, что если каждый импульс принятой последовательности имеет вид sinc(t/T), импульсы могут детектироваться без МСИ. На рисунке 3 б) показано, как можно обойти МСИ. Итак, имеем два импульса h(t) и h(t – T). Несмотря на то, что хвосты функции h(t) имеют бесконечную длительность, из рисунка видно, что в момент t = T взятия выборки функции h(t – T) хвост функции h(t) проходит через точку нулевой амплитуды, и подобным образом он будет иметь нулевую амплитуду в моменты взятия выборок всех остальных импульсов последовательности
h(t – kT), k = ±1, ±2, … . Таким образом, хвосты предыдущих импульсов не оказывают влияние на принятие решения детектором.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.