Разработка проекта железобетонного моста (пролёт главной балки – 3300 см), страница 3

M≤M_lim , где

M – максимальный расчётный момент внешних сил;

M_lim – максимальный (предельный) момент внутренних сил.

M_lim=R_sA_sz , где z – плечо внутренний пары сил.

h₀=h - a_p =160 - 20=140 см.

z=h₀ - =140 - =130 см.

A_p≥==60.22 см²

A_p1=n·24· см²

n – число проволок в пучке.

n_n – число пучков.

n_n=

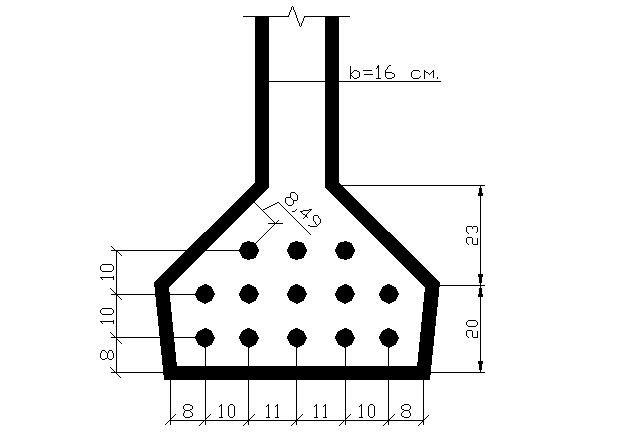
Рис. 5

Расчёт на прочность по изгибаемому моменту сечений, нормальных к продольной оси элемента.

Цель расчёта – гарантировать конструкцию от разрушения при действии наиболее тяжёлой расчётной эксплуатационной нагрузки.

 см.

 см.

Условие прочности (первая группа предельных состояний):

M≤R_b··x·(h₀-0.5x)+R_sc·(h₀-)+, где х определяется по следующей формуле:

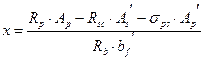, причём наибольшие напряжения в напрягаемой арматуре, расположенной в сжатой зоне,определяются по формуле:

, где- учитываемое расчётом наибольшее сжимающие напряжение          в  напрягаемой арматуре (≤5100 кг/см²), а =0.75·10150·1.1=8373.8 кг/см²

=5100-8373.8 = -3273.8 кг/см²

см.

Рис. 6

≤255·210·11.5·(140-0.5·11.5)+ 3450·10.56·(140-10)- 2512.5·9.43(140-8)

≤83388201 => условие выполнено

Приведённые формулы справедливы при:

, где- относительная высота сжатой зоны бетона, определяемая по

СНиП 2.05.03-84^*, п. 3.61

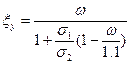, где ,=R_p+5100-,=5100 кг/см²

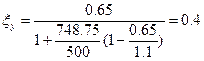
  0,08≤0.4 => условие выполнено

Определение приведённых геометрических характеристик сечения.

n_17=;      E_p=1.8·10⁶ кг/см², E_b=398·10³ кг/см²

n₁₇=4.52

n_17=;      E_s=2.0·10⁶ кг/см², E_b=398·10³ кг/см²

n₁₇=5.14

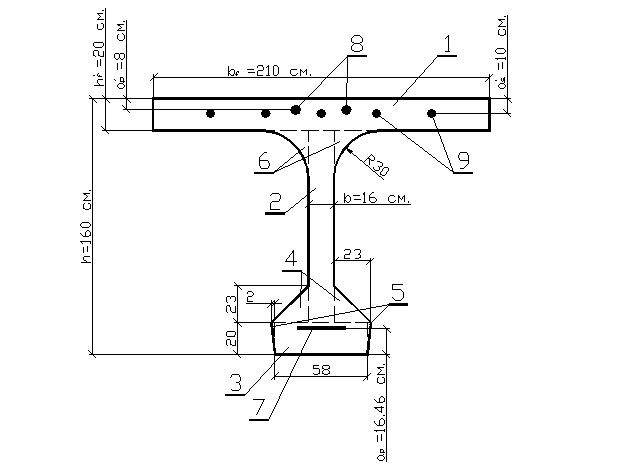
Рис. 7

Расчёт по образованию трещин, нормальных к продольной оси элемента в стадии эксплуатации.

Цель расчёта – обеспечение высокой надёжности конструкции против образования поперечных трещин или их ограниченного раскрытия в растянутой от внешней нагрузки зоне. В результате расчёта определяются эффективные напряжения σ_p1 в арматуре на стадии эксплуатации, обеспечивающие поперечную трещиностойкость.

Условия трещиностойкости: σ_bt≤k·R_bt,n , где σ_bt – растягивающее (после протекания потерь)

напряжения  в бетоне растянутой зоны.

Для автодороги k=1.4

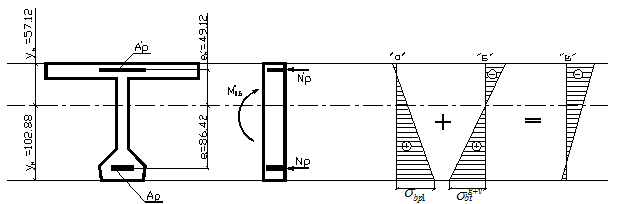
Рис. 8

Эпюры нормальных напряжений «а» - от обжатия, «б» - от внешней нагрузки,

«в» - суммарная.

Для конструкций с натяжением арматуры на упоры σ_bp1 и σ_p1 связаны зависимостью:

 (*)

где σ_bp1 -  величина сжимающих предварительных напряжений в бетоне нижней фибры от усилия натяжения арматуры.

Растягивающие напряжения в нижней фибре от внешних постоянных и временных нагрузок:

 кг/см²  

= 220.87-1.4·23.5=187.97 кг/см²  

Для бетона В 50 R_bt,n=23.5 кг/см²  

 

Из формулы (*) получим величину установившихся (после потерь) предварительных напряжений в арматуре:

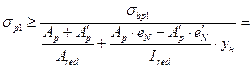
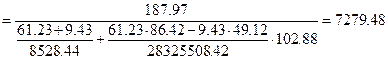 кг/см²  

Найденные напряжения в арматуре обеспечивают требования по трещиностойкости сечений нормальных к продольной оси балки в стадии эксплуатации.

  Определение потерь предварительно напряжения арматуры и контролируемых напряжений в арматуре в стадии эксплуатации.Расчет арматуры на прочность на стадии изготовления.

После напряжения арматуры, в ней начинают протекать процессы, приводящие к потере предварительных напряжений. Все потери делятся на две группы:

1)  - потери, протекающие в период изготовления конструкции. 

2)  - потери, протекающие в период эксплуатации конструкции. 

Общие потери 1.   

Контролируемые напряжения в арматуре:

σ_p=1.1·R_p=1.1·10150=11165 кг/см²

1. Потери σ₁ от релаксации напряжений арматуры при механическом способе натяжения:

    900 кг/см²

R_p,n – нормативное сопротивление расширению (R_p,n=13600 кг/см²)

2. Потери σ₂ от температурного периода при натяжении на упоры:

, где  при отсутствии точных данных о перепаде температур равняется 65^о С

σ₂=65·10.2=663 кг/см²

 

3. Потери σ₃ от деформации анкеров, расположенных у напряжённых устройств при напряжении на упоры:

, где Δl = 2·0.2=0.4 см, l_y – длина напрягаемого арматурного элемента.

l_y=l_п+(1.5÷2.0)=33+1.6=34.6 м

E_p=1.8·10⁶  

208 кг/см²

 

4. Потери σ₄ от трения арматуры:

σ₄=0 кг/см²