







6.Диаграммы растяжения (сжатия).
Для изучения свойств материалов и их способности выдерживать нагрузки на растяжение (сжатие) производят испытание образцов материалов вплоть до их разрушения. Наибольшее распространение имеют испытания на растяжение медленно меняющейся (статической) нагрузкой. При испытании цилиндрических образцов основными являются образцы диаметром 10мм.
При испытаниях автоматически записывается
зависимость между нормальным напряжением в поперечном сечении образца ![]() и относительным удлинением образца
и относительным удлинением образца ![]() .
.
Здесь F0 и l0 – первоначальные значения площади и длины образца; ![]() - абсолютное изменение длины
образца.
- абсолютное изменение длины
образца.
В качестве примера рассмотрим диаграмму растяжения образца из малоуглеродистой (пластичной) стали. Диаграмма имеет вид, представленный на рис.8.

Рис.8
На рис.8 введены следующие условные обозначения:
σрч – предел
пропорциональности (диапазон применения закона Гука), σрч![]() 210ГПа;
210ГПа;
σв – предел упругости (при разгрузке образец
восстанавливает свою форму), σв![]() 220
Гпа;
220
Гпа;
участок CD – площадка текучести.
σу – предел
текучести – напряжение, выше которого происходит рост деформации без увеличения
нагрузки, σу![]() 230 ГПа.
230 ГПа.
Напряжение, при котором остаточная деформация равна 0.2 %, называется условным пределом текучести и обозначается σ0.2.
По мере роста напряжения происходит перестроение кристаллов (происходит ориентирование осей кристаллов вдоль оси растяжения), в результате которого материал снова приобретает способность сопротивляться растяжению (упрочняется) - за точкой D;
σи – предел прочности (определяется как
напряжение, соответствующее наибольшей нагрузке, предшествующей разрушению
образца), σи![]() 380 МПа.
380 МПа.
За σи на образце появляется местное сужение, называемое шейкой, площадь сечения образца быстро уменьшается и, как следствие, падает усилие и напряжение. Разрыв образца происходит по наименьшему сечению шейки.
Если при нагружении образца предел упругости не был
превышен, то при разгружении все деформации полностью исчезают. Если предел
упругости был превышен (например, точка К), то разгрузка пойдет по
прямой KL, параллельной OA. Упругая часть деформации (отрезок LM)
исчезнет, пластическая часть деформации (отрезок OL)
останется. Если материал нагружать снова, то диаграмма пойдет по прямой LK.
Т.е. в этом случае уровень предела пропорциональности повышается. Данное
явление называется наклепом (![]() >σрч) и широко
используется на практике для расширения диапазона упругой деформации.
>σрч) и широко
используется на практике для расширения диапазона упругой деформации.
На практике фактические нагрузки, действующие на деталь, а также свойства материалов, из которых она изготовлена, могут значительно отличаться от тех, которые принимаются для расчета. Различного рода непредусмотренные перегрузки, неоднородности материала, носящие случайный характер, не могут быть предварительно учтены. Так как изделия должны безопасно работать и при этих неблагоприятных условиях, то при расчетах вводят так называемый коэффициент запаса прочности или коэффициент безопасности n:
![]() , где σadm– допускаемое напряжение (при
дальнейшем изложении допускаемые напряжения будем обозначать к квадратных
скобках
, где σadm– допускаемое напряжение (при
дальнейшем изложении допускаемые напряжения будем обозначать к квадратных
скобках![]() ).
).
Значения коэффициента безопасности обычно принимают на основании опыта конструирования и эксплуатации изделий определенного типа. Если материал хорошо известен и стабилен по характеристикам, то коэффициент запаса берут равным 1.2 – 1.5; если не совсем уверены в свойствах - n = 2 – 4; если вообще неясно, в каких условиях будет работать изделие, то n берут 10 – 14.
Таким образом, условие прочности при растяжении (сжатии) записывается в виде:
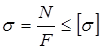 .
.
Пользуясь этим условием, можно:
1. Проверять прочность стержня при заданной нагрузке и известных размерах стержня.
2. Определять размеры поперечного сечения стержня при известной нагрузке и допускаемому напряжению (т.е. при выбранном материале).
3. Определять допустимую продольную силу при заданных размерах поперечного сечения и известному допускаемому напряжению.
7. Напряжения в наклонных сечениях.
Рассмотрим случай осевого растяжения стержня (рис.9). Считаем известными нормальные напряжения σ в поперечном сечении стержня, т.е.
![]() .
.
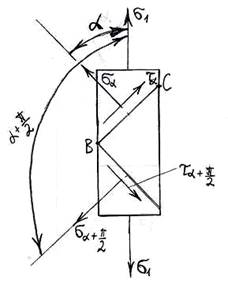
Рис.9
Определим напряжение в наклонном сечении BC, развернутом относительно направления σ на угол α (угол положителен, если поворот нормали к сечению осуществляется обратно движению часовой стрелки).
Площадь стержня в наклонном сечении:
![]() (*).
(*).
Рассечем мысленно стержень по сечению ВС и отбросим
верхнюю часть (рис.10). В общем случае в наклонном сечении могут действовать
нормальные σα и касательные τα напряжения. Их значения находим из условия равновесия
отсеченной (нижней) части:![]()
![]() .
.
(сумма сил на направление σα должна равняться нулю).
Учитывая выражение (*), получим:
![]() .
.
Проецируя силы на направление τα, по аналогии получим:
![]() ,
,
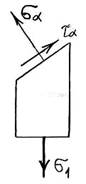
Рис.10
откуда ![]() .
.
Из анализа полученных выражений видно, что при α
= 0 нормальные напряжения достигают максимума, а касательные равны нулю. При α
=![]() σ = 0 и τ = 0,
т.е. в продольных сечениях нет ни нормальных, ни касательных напряжений. При
α =
σ = 0 и τ = 0,
т.е. в продольных сечениях нет ни нормальных, ни касательных напряжений. При
α =![]() касательное напряжение достигает
максимума и равно τmax =
касательное напряжение достигает
максимума и равно τmax =![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.