Диаграммы растяжения (сжатия). Действительное напряженное состояние равновесия упругого тела (системы), страница 2

Для взаимно перпендикулярной площадки, т.е. при угле  будем иметь:

.

Анализируя полученные результаты, видим, что:

, т.е. сумма нормальных напряжений по двум взаимно перпендикулярным площадкам, развернутым на угол α относительно главного напряжения, постоянна и равна главному напряжению;

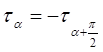, т.е. на двух взаимно перпендикулярных площадках действуют равные по величине и обратные по знаку касательные напряжения (закон парности или закон взаимности касательных напряжений).

Касательные напряжения на двух взаимно перпендикулярных площадках направлены оба либо к ребру пересечения площадок, либо от ребра.

Если нормаль к площадке для совпадения с направлением касательного напряжения необходимо поворачивать против часовой стрелки, то касательное напряжение считается отрицательным и наоборот.

8. Работа внешних и внутренних сил при растяжении (сжатии).

Рассмотрим случай статически приложенной внешней силы, т.е. такой, которая растет в процессе деформации от нуля до своего конечного значения с небольшой скоростью (рис.11-а).

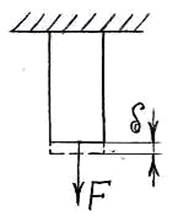
а)                                                                 б)

Рис.11

Элементарная работа dW внешней силы P на элементарном приращении перемещения dδ равна:

                                           (**).

Но в соответствии с законом Гука текущее значение удлинения стержня под действием нагрузки P (рис.11-б):

, откуда , поэтому , где F – площадь поперечного сечения .

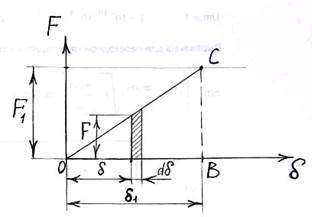
Полная работа конечного значения силы P₁на полном перемещении δ₁  определится путем интегрирования:

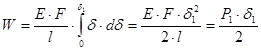, т.е.

Из последнего выражения видно, что работа внешней статически приложенной силы равна половине произведения окончательного значения силы на окончательную величину соответствующего перемещения (графически – площадь DOCB диаграммы рис.11-б).

Следует особо обратить внимание на то, что работа силы F₁, неизменной по значению, на перемещении δ₁ равна:

, т.е. в два раза больше, чем при статическом воздействии.

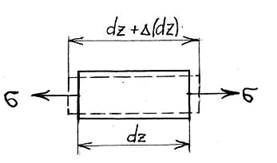
Определим работу внутренних сил при воздействии статически приложенной нагрузки. Для этого рассмотрим элемент стержня длиной dz, подвергнутого растяжению (рис.12). На элемент  dz действуют нормальные напряжения σ, являющиеся для него внешними силами. При этом элемент dzполучает приращение длины .  

Элементарная работа внутренних сил определится из выражения:

, где - равнодействующая нормального растягивающего усилия. Знак минус перед выражением учитывает тот факт, что внутренние усилия стержня сопротивляются растяжению стержня, т.е. направлены в противоположную сторону N.

Рис.12

Согласно закону Гука:

, следовательно

.

Полная работа внутренних сил определится после интегрирования последнего выражения по всей длине стержня l:

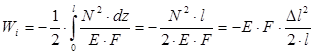,  где  - полное удлинение стержня.

Величина, равная работе внутренних сил, но имеющая противоположный знак, называется потенциальной энергией деформации (накопленная телом энергия при деформации):

.

Удельная потенциальная энергия (на единицу объема) определится из выражения:

.

Или   (т.к. ) или , где ε – относительное удлинение.

Укажем два важных свойства механической энергии:

1.     Суммарная работа внешних и внутренних сил при упругой деформации тела равна нулю, т.е.

, где

W – работа внешних сил («+» при нагружении),

Wi – работа внутренних сил («-» при нагружении).

Учитывая, что, можно записать:

.

2.     Действительное напряженное состояние равновесия упругого тела (системы) отличается от всех сложных состояний равновесия тем, что оно дает минимум потенциальной энергии деформации.

Например, если потенциальная энергия зависит от неизвестных усилий X₁, X₂,... то все неизвестные можно определить из условия минимума энергии:

; ; …

Данное свойство широко используется при решении статически неопределимых задач.

Пример. Рассчитатьусилия в шарнирно соединенных стержнях (рис.13), находящихся под действием нагрузки P.

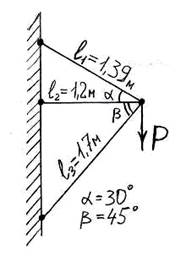
F₁ = 3.14 см²,

F₂ = 3.14 см²,

F₃ = 21.9 см².

Рис.13

Данная система один раз статически неопределима, поскольку можно составить только два уравнения статического равновесия, а неизвестных усилий три. Для решения задачи поступим следующим образом. Перерезаем мысленно стержень 3. Реакцию отброшенного стержня примем растягивающей и обозначим ее через продольную силу Х (рис.14).

                        

Рис.14

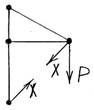
Определим усилия в оставшихся стержнях от действия усилия X (рис.15). Для этого мысленно разрежем стержни 1 и 2 и составим уравнения равновесия системы.

           

Рис.15

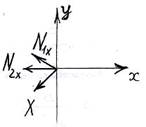
;                     , откуда

(растяжение).

;    , откуда

 (сжатие).

Теперь, поступая по аналогии,  определим усилия в стержнях 1 и 2 под действием нагрузки P(рис.15).

;        ;

 (растяжение);

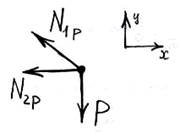
Рис.15

;    ;

 (сжатие).

Определяем суммарные усилия в стержнях под действием нагрузки P:

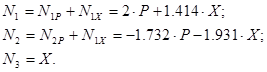
Определяем потенциальную энергию деформации:

.

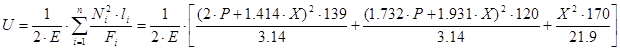Значение усилия X определим из условия минимума потенциальной энергии деформации:

,

откуда  (сжатие).

 (растяжение).

 (растяжение).

Таким образом, использование условия минимума потенциальной энергии деформации позволило раскрыть статическую неопределенность нагруженной системы и определить усилия в стержнях.