





Программа по математике предназначена для учащихся выпускных классов одногодичного потока СУНЦ НГУ, способствует углубленному изучению программы общеобразовательной школы, обеспечивает основы для получения фундаментального математического образования, способствует расширению математического кругозора и раннему развитию научных интересов школьников.
Курс содержит элементы логики, операции над множествами, свойства числовых множеств, понятия функции, предела последовательности, предела функции, свойства непрерывных функций, понятие производной и интеграла, дает основные операции над комплексными числами и многочленами. В курсе рассматриваются элементы векторной алгебры и метод координат на плоскости и в пространстве. Значительное внимание уделяется практическому применению теории при решении задач, геометрической интерпретации основных положений теории, получению практических навыков, завершению общеобразовательной подготовки, в том числе подготовки к ЕГЭ.
В результате освоения курса обучающийся должен: знать основные положения курса, формулировки определений и теорем, схемы и методы доказательств; уметь использовать приобретенные знания в практической деятельности и повседневной жизни, выполнять вычисления и преобразования, решать уравнения и неравенства, выполнять действия с функциями, с геометрическими фигурами, координатами и векторами, строить и исследовать математические модели, владеть калькулятором, компьютером, чертежными инструментами, чтением графиков функций.
Предусмотрены следующие формы организации учебного процесса: практические занятия, включающие самостоятельную работу учащегося, контрольная работа, консультация.
Предусмотрены следующие виды контроля: текущий контроль успеваемости в форме контрольной работы, месячного балла, промежуточный контроль в форме зачета, промежуточный контроль в форме письменного и устного экзаменов.
Рабочая программа семинарских занятий на 170 часов составлена на основе разработанной Ляпуновым И. Б. авторской программы по математике для учащихся одногодичного химико-биологического потока СУНЦ НГУ, 11 классов.
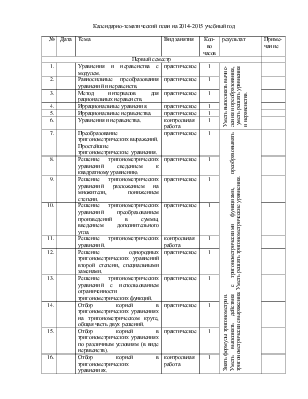
Календарно-тематический план на 2014-2015 учебный год
|
№ |
Дата |
Тема |
Вид занятия |
Кол-во часов |
результат |
Приме-чание |
|
Первый семестр |
||||||
|
1. |
Уравнения и неравенства с модулем. |
практическое |
1 |
Уметь выполнять вычис-ления и преобразования, уметь решать уравнения и неравенства. |
||
|
2. |
Равносильные преобразования уравнений и неравенств. |
практическое |
1 |
|||
|
3. |
Метод интервалов для рациональных неравенств. |
практическое |
1 |
|||
|
4. |
Иррациональные уравнения. |
практическое |
1 |
|||
|
5. |
Иррациональные неравенства. |
практическое |
1 |
|||
|
6. |
Уравнения и неравенства. |
контрольная работа |
1 |
|||
|
7. |
Преобразование тригонометрических выражений. Простейшие тригонометрические уравнения. |
практическое |
1 |
Знать формулы тригонометрии. Уметь выполнять действия с тригонометрическими функциями, преобразовывать тригонометрические выражения. Уметь решать тригонометрические уравнения. |
||
|
8. |
Решение тригонометрических уравнений сведением к квадратному уравнению. |
практическое |
1 |
|||
|
9. |
Решение тригонометрических уравнений разложением на множители, понижением степени. |
практическое |
1 |
|||
|
10. |
Решение тригонометрических уравнений преобразованием произведений в суммы, введением дополнительного угла. |
практическое |
1 |
|||
|
11. |
Решение тригонометрических уравнений. |
контрольная работа |
1 |
|||
|
12. |
Решение однородных тригонометрических уравнений второй степени, специальными заменами. |
практическое |
1 |
|||
|
13. |
Решение тригонометрических уравнений с использованием ограниченности тригонометрических функций. |
практическое |
1 |
|||
|
14. |
Отбор корней в тригонометрических уравнениях на тригонометрическом круге, общая часть двух решений. |
практическое |
1 |
|||
|
15. |
Отбор корней в тригонометрических уравнениях по различным условиям (в виде неравенств). |
практическое |
1 |
|||
|
16. |
Отбор корней в тригонометрических уравнениях. |
контрольная работа |
1 |
|||
|
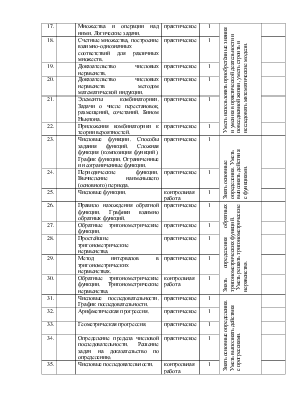
17. |
Множества и операции над ними. Логические задачи. |
практическое |
1 |
Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать математические модели. |
||
|
18. |
Счетные множества, построение взаимно-однозначных соответствий для различных множеств. |
практическое |
1 |
|||
|
19. |
Доказательство числовых неравенств. |
практическое |
1 |
|||
|
20. |
Доказательство числовых неравенств методом математической индукции. |
практическое |
1 |
|||
|
21. |
Элементы комбинаторики. Задачи о числе перестановок, размещений, сочетаний. Бином Ньютона. |
практическое |
1 |
|||
|
22. |
Приложения комбинаторики к теории вероятностей. |
практическое |
1 |
|||
|
23. |
Числовые функции. Способы задания функций. Сложная функция (композиция функций). График функции. Ограниченные и неограниченные функции. |
практическое |
1 |
Знать основные определения. Уметь выполнять действия с функциями. |
||
|
24. |
Периодические функции. Вычисление наименьшего (основного) периода. |
практическое |
1 |
|||
|
25. |
Числовые функции. |
контрольная работа |
1 |
|||
|
26. |
Правило нахождения обратной функции. Графики взаимно обратных функций. |
практическое |
1 |
Знать определения обратных тригонометрических функций. Уметь решать тригонометрические неравенства. |
||
|
27. |
Обратные тригонометрические функции. |
практическое |
1 |
|||
|
28. |
Простейшие тригонометрические неравенства. |
практическое |
1 |
|||
|
29. |
Метод интервалов в тригонометрических неравенствах. |
практическое |
1 |
|||
|
30. |
Обратные тригонометрические функции. Тригонометрические неравенства. |
контрольная работа |
1 |
|||
|
31. |
Числовые последовательности. График последовательности. |
практическое |
1 |
Знать основные определения. Уметь выполнять действия с прогрессиями. |
||
|
32. |
Арифметическая прогрессия. |
практическое |
1 |
|||
|
33. |
Геометрическая прогрессия. |
практическое |
1 |
|||
|
34. |
Определение предела числовой последовательности. Решение задач на доказательство по определению. |
практическое |
1 |
|||
|
35. |
Числовые последовательности. |
контрольная работа |
1 |
|||
|
36. |
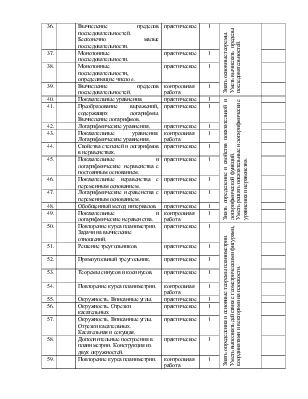
Вычисление пределов последовательностей. Бесконечно малые последовательности. |
практическое |
1 |
Знать основные теоремы. Уметь вычислять пределы последовательностей. |
||
|
37. |
Монотонные последовательности. |
практическое |
1 |
|||
|
38. |
Монотонные последовательности, определяющие число e. |
практическое |
1 |
|||
|
39. |
Вычисление пределов последовательностей. |
контрольная работа |
1 |
|||
|
40. |
Показательные уравнения. |
практическое |
1 |
Знать определение и свойства показательной и логарифмической функций. Уметь решать показательные и логарифмические уравнения и неравенства. |
||
|
41. |
Преобразование выражений, содержащих логарифмы. Вычисление логарифмов. |
практическое |
1 |
|||
|
42. |
Логарифмические уравнения. |
практическое |
1 |
|||
|
43. |
Показательные уравнения. Логарифмические уравнения. |
контрольная работа |
1 |
|||
|
44. |
Свойства степеней и логарифмов в неравенствах. |
практическое |
1 |
|||
|
45. |
Показательные и логарифмические неравенства с постоянным основанием. |
практическое |
1 |
|||
|
46. |
Показательные неравенства с переменным основанием. |
практическое |
1 |
|||
|
47. |
Логарифмические неравенства с переменным основанием. |
практическое |
1 |
|||
|
48. |
Обобщенный метод интервалов. |
практическое |
1 |
|||
|
49. |
Показательные и логарифмические неравенства. |
контрольная работа |
1 |
|||
|
50. |
Повторение курса планиметрии. Задачи на вычисление отношений. |
практическое |
1 |
Знать определения и основные теоремы планиметрии. Уметь выполнять действия с геометрическими фигурами, координатами и векторами на плоскости. |
||
|
51. |
Решение треугольников. |
практическое |
1 |
|||
|
52. |
Прямоугольный треугольник. |
практическое |
1 |
|||
|
53. |
Теоремы синусов и косинусов. |
практическое |
1 |
|||
|
54. |
Повторение курса планиметрии. |
контрольная работа |
1 |
|||
|
55. |
Окружность. Вписанные углы. |
практическое |
1 |
|||
|
56. |
Окружность. Отрезки касательных. |
практическое |
1 |
|||
|
57. |
Окружность. Вписанные углы. Отрезки касательных. Касательная и секущая. |
практическое |
1 |
|||
|
58. |
Дополнительные построения в планиметрии. Конструкция из двух окружностей. |
практическое |
1 |
|||
|
59. |
Повторение курса планиметрии. |
контрольная работа |
1 |
|||
|
60. |
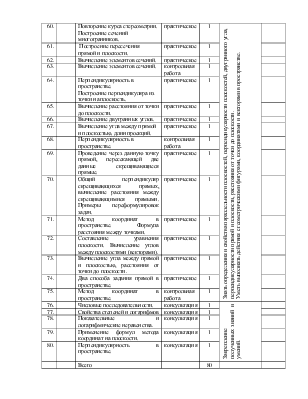
Повторение курса стереометрии. Построение сечений многогранников. |
практическое |
1 |
Знать определения и свойства параллельности плоскостей, перпендикулярности плоскостей, двугранного угла, перпендикулярности прямой и плоскости, расстояния от точки до плоскости. Уметь выполнять действия с геометрическими фигурами, координатами и векторами в пространстве. |
||
|
61. |
Построение пересечения прямой и плоскости. |
практическое |
1 |
|||
|
62. |
Вычисление элементов сечений. |
практическое |
1 |
|||
|
63. |
Вычисление элементов сечений. |
контрольная работа |
1 |
|||
|
64. |
Перпендикулярность в пространстве. Построение перпендикуляра из точки на плоскость. |
практическое |
1 |
|||
|
65. |
Вычисление расстояния от точки до плоскости. |
практическое |
1 |
|||
|
66. |
Вычисление двугранных углов. |
практическое |
1 |
|||
|
67. |
Вычисление угла между прямой и плоскостью, длин проекций. |
практическое |
1 |
|||
|
68. |
Перпендикулярность в пространстве. |
контрольная работа |
1 |
|||
|
69. |
Проведение через данную точку прямой, пересекающей две данные скрещивающиеся прямые. |
практическое |
1 |
|||
|
70. |
Общий перпендикуляр скрещивающихся прямых, вычисление расстояния между скрещивающимися прямыми. Примеры переформулировок задач. |
практическое |
1 |
|||
|
71. |
Метод координат в пространстве. Формула расстояния между точками. |
практическое |
1 |
|||
|
72. |
Составление уравнения плоскости. Вычисление углов между плоскостями (векторами). |
практическое |
1 |
|||
|
73. |
Вычисление угла между прямой и плоскостью, расстояния от точки до плоскости. |
практическое |
1 |
|||
|
74. |
Два способа задания прямой в пространстве. |
практическое |
1 |
|||
|
75. |
Метод координат в пространстве. |
контрольная работа |
1 |
|||
|
76. |
Числовые последовательности. |
консультация |
1 |
Закрепление полученных знаний и умений. |
||
|
77. |
Свойства степеней и логарифмов |
консультация |
1 |
|||
|
78. |
Показательные и логарифмические неравенства. |
консультация |
1 |
|||
|
79. |
Применение формул метода координат на плоскости. |
консультация |
1 |
|||
|
80. |
Перпендикулярность в пространстве. |
консультация |
1 |
|||
|
Всего |
80 |
|||||
|
Письменный экзамен. |
экзамен |
6 |
Оценка уме-ний и навыков |
|||
|
Устный экзамен. |
экзамен |
2 |
Оценка знаний теории |
|||
|
Итого за первый семестр |
88 |
|||||
|
Второй семестр |
||||||
|
81. |
Вычисление пределов функций на бесконечности. |
практическое |
1 |
Знать основные понятия теории предела функции. Уметь выполнять вычисления пределов и преобразования. |
||
|
82. |
Асимптоты на бесконечности. |
практическое |
1 |
|||
|
83. |
Вычисление пределов функций. |
контрольная работа |
1 |
|||
|
84. |
Два определения предела функции в точке. Решение задач на доказательство предела по определению. |
практическое |
1 |
|||
|
85. |
Вычисление пределов функций в точке. |
практическое |
1 |
|||
|
86. |
Вычисление пределов функций в точке. |
контрольная работа |
1 |
|||
|
87. |
Непрерывные функции |
практическое |
1 |
|||
|
88. |
Использование непрерывности при вычислении пределов. Применение первого и второго замечательных пределов. |
практическое |
1 |
|||
|
89. |
Односторонние пределы. Вертикальные асимптоты. |
практическое |
1 |
|||
|
90. |
Вычисление пределов функций в точке с использованием замечательных пределов. |
контрольная работа |
1 |
|||
|
91. |
Производная. Операции. Дифференцирование по таблице. |
практическое |
1 |
Знать основные понятия теории производной функции. Уметь выполнять вычисления производной и преобразования, исследовать | ||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.