Аналитические методы оптимизации. Решение задачи оптимизации с ограничениями типа равенств

Задание №1. Аналитические методы оптимизации.

Задача 1. Найти экстремум квадратичной функции . Изобразить в масштабе на плоскости  не менее пяти линий постоянного уровня около ее точки минимума (заполнить всю плоскость).

Решение.

Решается задача безусловной оптимизации.

1.  Реализация необходимого условия оптимальности.

Для того, чтобы точка  была точкой безусловного локального экстремума функции  (функция дифференцируема в окрестности этой точки), необходимо чтобы выполнялось равенство . То есть вектор градиента функции в этой точке должен быть нулевым.

Находим градиент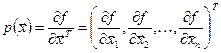

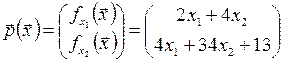
Приравнивая к нулю полученные частные производные, получаем систему двух линейных алгебраических уравнений с двумя переменными.

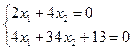
Решая эту систему, получаем единственную стационарную точку

2. Реализация достаточного условия оптимальности.

Второй дифференциал  есть квадратичная форма , где

·  Если квадратичная форма положительно определенная, точка является точкой строгого локального минимума.

·  Если квадратичная форма отрицательно определенная, точка является точкой строгого локального максимума.

·  Если квадратичная форма не определена, то в точке нет экстремума

·  Если квадратичная форма определена неотрицательно (неположительно) (может обращаться в нуль для некоторых ), то нельзя сказать ничего определенного о наличии или отсутствия локального экстремума в этой точке.

В скалярном виде квадратичная форма записывается следующим образом:

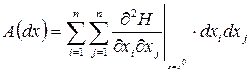, где 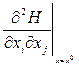- элементы матрицы Гессе

Находим матрицу Гессе, дифференцируя первые производные:

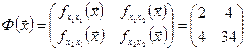
Так как функция квадратичная, то вторые частные производные постоянны и не зависят от координат точки, для которой они вычисляются.

В соответствии с критерием Сильвестра для того, чтобы квадратичная форма с симметричной матрицей  была положительно определена, необходимо и достаточно, чтобы все главные миноры ее матрицы были положительны. Для отрицательной определенности формы необходимо и достаточно, чтобы главные миноры нечетного порядка ее матрицы  были отрицательны, а главные миноры четного порядка  - положительны.

Так как все главные миноры матрицы Гессе данного и ее определитель положительны, следовательно, функция имеет в точке локальный минимум:

Так как точка одна, следовательно, локальный минимум является также и глобальным.

3.Построение линий постоянного уровня (ЛПУ).

1) Рассчитываем вспомогательные параметры:

,   ,

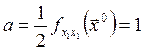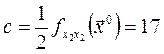
2) Рассчитываем собственные числа матрицы Гессе.

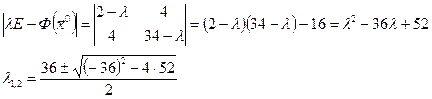
3) Рассчитываем вспомогательные константы для построения ЛПУ.

,

Полученные b равны собственным числам матрицы Гессе, следовательно, вычисления верны.

Полученные ЛПУ являются эллипсами

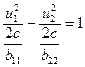, с – константа где u – координаты на новой системе координат, полученной смещением системы на координаты стационарной точки  и поворотом ее на угол α.

Ответ: Глобальный минимум функции  в точке 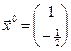, значение функции в этой точке

Задача 2. Решить задачу оптимизации с ограничениями типа равенств. Графически и аналитически оптимизировать функцию  при наличии ограничения типа равенства . Определить максимум или минимум достигается в оптимальной точке.

Решение.

Решается задача оптимизации с ограничением типа равенства методом множителей Лагранжа.

1. Реализация необходимого условия оптимизации.

Формируется функция Лагранжа:

, где

 - неизвестные постоянные – множители Лагранжа.

В векторной форме функция Лагранжа записывается так:

Множество точек услового минимума  совпадает с множеством точек безусловного минимума функции Лагранжа.

При решении задача безусловной оптимизации для функции Лагранжа (H) размерность задачи с n увеличивается до n+m, n – количество составляющих вектора x, m – количество связывающих уравнений. В невырожденных случаях только n-m переменных x_i являются независимыми, остальные m зависимые.

В нашем случае:

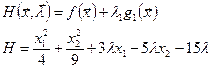
Необходимое условие в скалярной форме для нашего случая:

, ,

Получаем систему линейных уравнений:

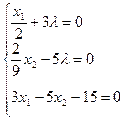
Решая ее, получаем:

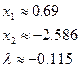
Стационарная точка:

2. Реализация достаточного условия локальной оптимизации.

Второй дифференциал функции Лагранжа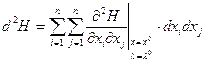

Формируем второй дифференциал функции Лагранжа: