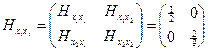
Непосредственно достаточные условия к
полученной матрице применить нельзя, так как не все переменные независимы. Выразив
из m зависимых дифференциалов через оставшиеся n-m независимых дифференциалов, после
подстановки их обратно во второй дифференциал функции Лагранжа и некоторых преобразований
формируется квадратичная форма n-m переменных ![]() :
: ![]() и ее матрица B есть матрица, составленная из коэффициентов
и ее матрица B есть матрица, составленная из коэффициентов ![]()
Для нашего случая:
Варьирование уравнения связи:
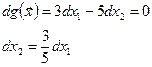
![]()
Матрица![]() -
следовательно, в точке
-
следовательно, в точке ![]() находится минимумом.
находится минимумом.
Ответ: Точка условной оптимизации с
ограничением типа равенства ![]() , точка
является минимумом, значение функции в этой точке
, точка
является минимумом, значение функции в этой точке ![]()
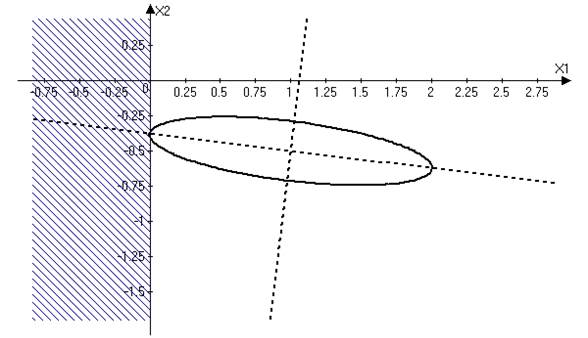
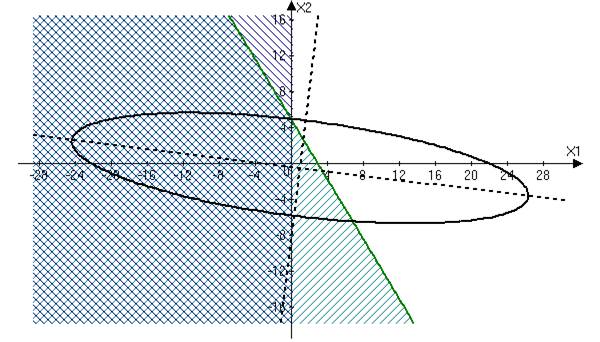
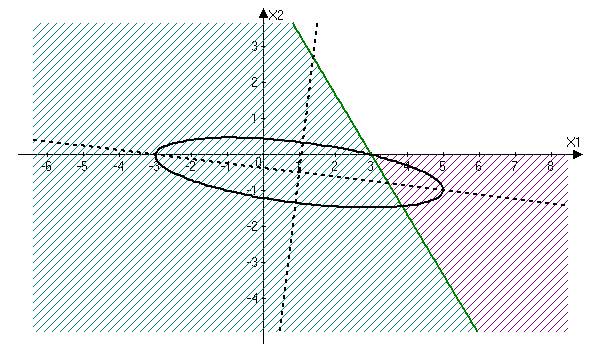
Задача 3. Графически и аналитически минимизировать квадратичную функцию задачи 1 при наличии ограничений типа неравенств:
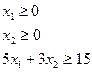
Указать на чертеже и выделить в ходе аналитического решения задачи все промежуточные точки, допустимые и недопустимые. Использовать семейство линий постоянного уровня функции задачи 1. Учесть, что при решении промежуточной задачи на условный экстремум при одном ограничении типа равенства в стационарной точке совпадают касательные к линии ограничения и соответствующей линии постоянного уровня целевой функции.
Решение.
Запишем ограничения в виде ![]() :
:
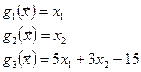
Для решения поставленной задачи формируется
функция Лагранжа от двух векторных переменных![]() и
и ![]()
Векторная форма: ![]()
Условие минимизации функции ![]() при наличии ограничений
при наличии ограничений ![]() в векторной форме имеет вид:
в векторной форме имеет вид:
![]() ,
, 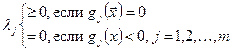
Фактически, решение задач оптимизации с ограничениями типа неравенств сводится к решению ряда задач абсолютной и условной оптимизации. Решение производится поэтапно. На первом этапе все множители Лагранжа приравниваются к нулю, это означает, что все ограничения неэффективны и решается задача абсолютной оптимизации функции. Второй этап – решается ряд задач оптимизации, когда один из множителей Лагранжа ненулевой, при этом одно из ограничений становится эффективным. Третий этап – решается ряд задач оптимизации, когда двое из множителей Лагранжа ненулевые и так далее поэтапно, пока все множители не будут отличны от нуля (задачи теряют смысл, когда n≥m). При этом на каждом этапе каждый полученный вектор проверяется ограничениями и недопустимые отбрасываются.
Этап 1. Решается задача абсолютной оптимизации функции.
Задача абсолютной оптимизации функции решалась в Задаче 1.
Стационарная точка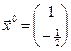 недопустима.
недопустима.
Этап 2. Решается задача оптимизации функции при одном ограничении типа равенства.
1) Эффективно первое ограничение
Для функции Лагранжа ![]() решаем задачу безусловной
оптимизации.
решаем задачу безусловной
оптимизации.
Система уравнений:
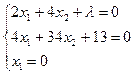
Решая систему, получаем ![]() ,
, ![]() ,
,
![]() . Проверяя по системе
ограничений, отбрасываем как недопустимую.
. Проверяя по системе
ограничений, отбрасываем как недопустимую.
2) Эффективно второе ограничение
Для функции Лагранжа ![]() решаем задачу безусловной
оптимизации.
решаем задачу безусловной
оптимизации.
Система уравнений:
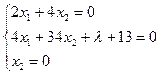
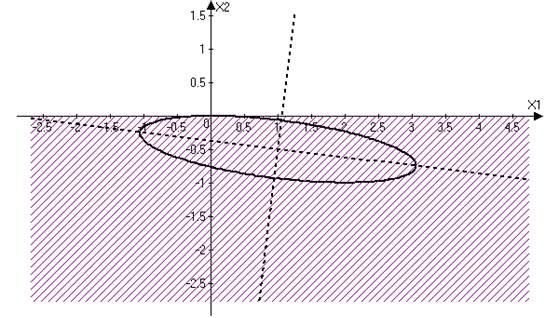
Решая систему, получаем ![]() ,
, ![]() ,
,
![]() . Проверяя по системе
ограничений, отбрасываем как недопустимую.
. Проверяя по системе
ограничений, отбрасываем как недопустимую.
3) Эффективно третье ограничение
Для функции Лагранжа ![]() решаем задачу безусловной
оптимизации.
решаем задачу безусловной
оптимизации.
Система уравнений:
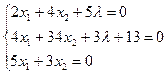
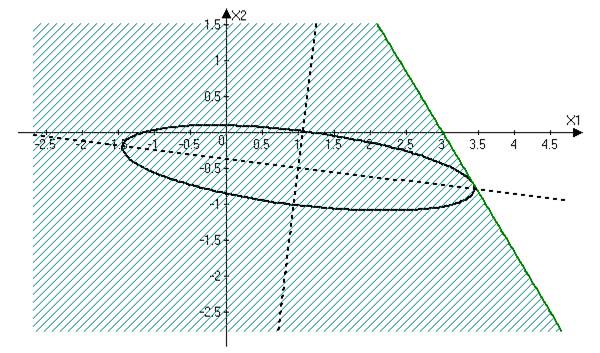
Решая систему, получаем ![]() ,
, ![]() ,
,
![]() . Проверяя по системе
ограничений, отбрасываем как недопустимую.
. Проверяя по системе
ограничений, отбрасываем как недопустимую.
Этап 3. Решается задача оптимизации функции при двух ограничениях типа равенства.
1) Эффективны первое и второе ограничения
Для функции Лагранжа ![]() решаем задачу безусловной
оптимизации.
решаем задачу безусловной
оптимизации.
Система уравнений:
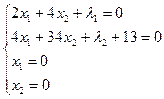

Решая систему, получаем ![]() ,
, ![]() ,
,
![]() . Такая точка уже была,
отбрасываем как недопустимую.
. Такая точка уже была,
отбрасываем как недопустимую.
2) Эффективны первое и третье ограничения
Для функции Лагранжа ![]() решаем задачу безусловной
оптимизации.
решаем задачу безусловной
оптимизации.
Система уравнений:
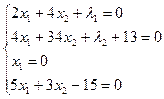
Решая систему, получаем ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
Точка принадлежит допустимой области решений. Значение функции в этой точке
.
Точка принадлежит допустимой области решений. Значение функции в этой точке ![]() .
.
3) Эффективны второе и третье ограничения
Для функции Лагранжа ![]() решаем задачу безусловной
оптимизации.
решаем задачу безусловной
оптимизации.
Система уравнений:
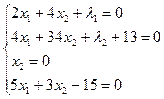
Решая систему, получаем ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
Точка принадлежит допустимой области решений. Значение функции в этой точке
.
Точка принадлежит допустимой области решений. Значение функции в этой точке ![]() .
.
Таким образом, получаем всего две допустимые точки:
![]() , значение
функции здесь
, значение
функции здесь ![]()
![]() , значение
функции здесь
, значение
функции здесь ![]()
Выбираем точку, ![]() где
значение функции минимально
где
значение функции минимально
Ответ. Оптимальная точка ![]() , значение функции в этой точке
, значение функции в этой точке
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.