|
Формулы сокращенного умножения:
1.
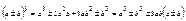
2.
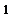 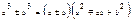
3.
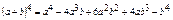
Схема Горнера:
Разделим многочлен f(x)=x3+5x2-3
на (x-5)
а=5; b2=a3=1; b1=b2*5+a2; b0=b1*5+a1, a1=0, не забыть, что не существующие члены принимаются за 0.
|
|
a3
|
a2
|
a1
|
a0
|
|
|
1
|
5
|
0
|
-3
|
|
5
|
1
|
10
|
50
|
247
|
|
|
b2
|
b1
|
b0
|
R
|
Точка минимума (максимума) квадратичной функции:  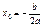
|
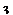 Тригонометрия: Тригонометрия:
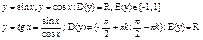
Основные формулы:
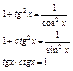
|
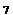 Уравнения
тригонометрические. Уравнения
тригонометрические.
|
|
|
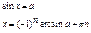
|
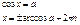
|
|
|
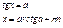
|
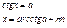
|
|
|
Значения тригонометрических функций:
|
|
0
|
30
p/6
|
45
p/4
|
60
p/3
|
90
p/2
|
180
p
|
270
3p/2
|
360
2p
|
|
sin
|
0
|
1/2
|
Ö2/2
|
Ö3/2
|
1
|
0
|
-1
|
0
|
|
cos
|
1
|
Ö3/2
|
Ö2/2
|
1/2
|
0
|
-1
|
0
|
1
|
|
tg
|
0
|
Ö3/3
|
1
|
Ö3
|
-
|
0
|
-
|
0
|
|
ctg
|
-
|
Ö3
|
1
|
Ö3/3
|
0
|
-
|
0
|
-
|
|
|
|
|
|
|
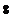 Логарифмы: Логарифмы:
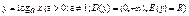
Основ. лог.
тождеств. 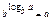
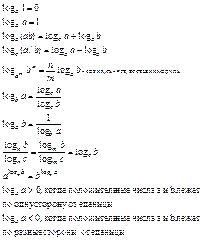
|
|
|
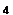 Формулы
сложения: Формулы
сложения:
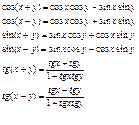
Формулы двойного и
тройного угла
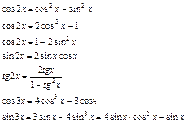
|
|
|
|
|
|
 Основные приемы преобразование графиков: Основные приемы преобразование графиков:
|
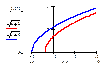
f(x+a)
|
Перенос графика f(x) влево на a
|
|
|
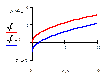
f(x)+b
|
Перенос графика f(x) вверх на a
|
|
|
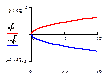
-f(x)
|
Симметрия относительно оси OX
|
|
|
f(-x)
|
Симметрия относительно оси OY
|
|
|
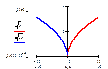
½f(x)½
|
Часть графика в верхней
полуплоскости и на оси OX без
изменения, а вместо части графика в нижней полуплоскости строим
симметричную ей относительно оси OX
|
|
|
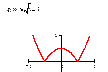
f(½x½)
|
Часть графика в правой полуплоскости и на оси OY без
изменения, а вместо части графика в левой полуплоскости строим симметричную
ей относительно оси OY
|
|
|
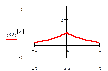
f(kx)
(k>0)
|
При k>1 сжатие к точке (0;0) вдоль оси OX в k
раз; при 0<k<1 растяжение от точки (0;0) вдоль оси OX в 1/k раз
|
|
|
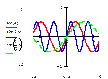
kf(x)
(k>0)
|
При k>1растяжение от точке (0;0) вдоль оси OY в k
раз; при 0<k<1 сжатие к точки (0;0) вдоль оси OY в
1/k раз
|
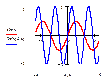
|
|
|
|
|
 Производная. Производная.
1.
Дифференцирование:
|
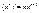
|
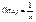
|
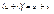
|
|
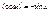
|
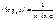
|
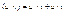
|
|
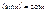
|
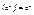
|
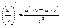
|
|
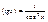
|
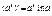
|
Уравнение касательной (не вертикальной к графику
функции y=f(x) в точке графика с абсциссой x0: 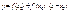
|
|
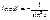
|
Производная сложной функции:
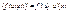
|
|
|
|
|
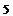 Формулы
понижения степени Формулы
понижения степени
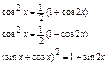
Универсальная
подстановка
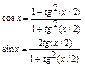 , не забыть про ОДЗ тангенса. , не забыть про ОДЗ тангенса.
|
|
|
 Суммы
в произведение Суммы
в произведение
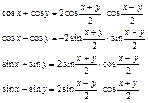
Произведение в сумму
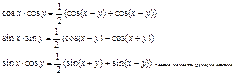 Формула дополнительного угла Формула дополнительного угла
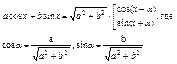
|
|
|
 Прогрессии Прогрессии
|
|
Арифметическая
|
Геометрическая
|
|
Формула общего
члена
|
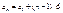
|
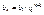
|
|
Характеристическое
свойство (исп. часто)
|
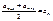
|
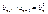
|
|
Формула суммы n
первых членов
|
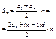
|
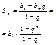
|
|
Другие формулы
|
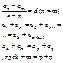
|
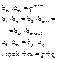
|
Формула суммы
бесконечно убывающий геометрической прогрессии (0<|q|<1): 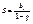
|
|
|
|
|