Треугольник, параллелограмм. Трапеция, равнобокая трапеция. Окружность. Нахождение биссектрис, медиан. Стереометрия

Треугольник:

        Биссектриса делит противолежащую сторону на отрезки, пропорциональные прилежащим  сторонам треугольника.

Средняя линия параллельна третьей стороне и равна ее половине.

Площадь треугольника:

, , где p- полупериметр, r – радиус вписан. окружности, R- описан. окруж.

Теорема косинусов:

Теорема синусов: , R - радиус описан. окружн.

Вписанная окружность: центр – точка пересеч. биссектрис , p – полупериметр.

Описанная окружность: центр – точка пересечения серединных перпендикуляров.

Прямоугольный треугольник: Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы. Центр описанной окружности совпадает с серединой гипотенузы.

Соотношения в прям. треугол:

Вычисл. радиусов описан. и вписан. окружности:

Правильный треугольник: Свойства: ,

Параллелограмм:

Доп. свойства: биссектриса угла параллелограмма отсекает от него равнобедренный треугольник; биссектрисы соседних углов параллелограмма перпендикулярны, а биссектрисы противоположных углов параллельны или лежат на одной прямой; диагонали параллелограмма делят его на четыре равновеликих треугольника.

- свойство диагоналей.

Площадь:

Ромб:

В ромб можно вписать окружность:

Площадь:

Прямоугольник:

Около прямоугольника можно описать окружность:

Площадь:

Квадрат:

Площадь квадрата:

Трапеция:

- средняя линия.

Площадь:

- отрезок, параллельный основаниям, проходящий через точку пересечения диагоналей.

- отрезок, параллельный основаниям и делящий трапецию на две равновеликие части.

В трапецию можно вписать окружность тогда и только тогда, когда сумма оснований равна сумме боковых сторон.

Равнобокая трапеция:

Свойства: Диагонали равнобокой трапеции равны.

Углы при одном основании равнобокой трапеции равны.

Только около равнобокой трапеции можно описать окружность; она совпадает с окружностью, описанной около любого треугольника с вершинами в вершинах трапеции; ее цент лежит на серединном перпендикуляре к основаниям трапеции.

Если центр описанной окружности лежит на основании трапеции, то ее диагональ перпендикулярна боковой стороне.

В равнобедренную трапецию можно вписать окружность, если боковая сторона равна средней линии.

Окружность:

Длина окружности: , Длина дуги, a - в радианах, j - в градусах

Площадь круга: Площадь сектора:

Площадь правильного n-угольника:

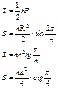
1.  Длина медианы треугольника:

Док-во: Достраиваем до параллелограмма и используем свойство диагоналей.

2.  Длина стороны треугольника: , где m_x – медианы треугольника.

Док-во: Достроим до новой фигуры, по свойству медиан треугольника:, из свойства диагоналей параллелограмма OBFC выразим a.

3.  Длина биссектрисы треугольника: (1.0)

Док-во: Применив теорему косинусов к треугольникам с равными углами BCD и ACD, составим уравнение: , далее преобразовываем, учитывая, что ab₁=a₁b (2.0)

4.  Длина биссектрисы треугольника через стороны:

Док-во: Запишем соотношение (1.0) в виде (3.0). Используя свойство (2.0), получаем, что , подставляем в формулу (3.0), получаем искомую.

5.  Зависимость между радиусом вписанной окружности и высотами треугольника.

Док-во: ,=> , p – полупериметр

6.  В равнобедренной трапеции, диагонали которой взаимно перпендикулярны  S=h²

Док-во: MN – перпендикуляр, являющийся осью симметрии трапеции. Т.к. ÐAOD=90⁰, то AD=2ON и BC=2OM =>

7.  Высота равнобедренный трапеции, в которую можно вписать окружность, является средним геометрическим ее основания.

Док-во: Т.к. в четырехугольнике, описанном около окружности, суммы длин противоположных сторон равны, то a+b=2c, оттуда . Далее, имеем  и из прям. треугол. ABE находим , т.е.

Стереометрия:

Призма: , V=S_оснH, V=S_^l?, P_^,S_^ - периметр, площадь перпендикулярный боковому ребру

Пирамида правильная: , где P – периметр основ. k – апофема,a - двугранный угол при ребре основания. V=1/3S_оснH– для любой пирамиды. - усеченная пирамида

Цилиндр: S_бок=2pRH, S_полн=2pR(R+H), V=S_оснH

Конус: S_бок=pRl, S_полн=2pR(R+l), l – образующая,

Усеченный конус: S_бок=p(R+r)l,

Шар и сфера: S=4pR², V=4/3pR³ , - объем сегмента, -шаровой сектор

Площади:

Некоторые соотношения площадей треугольников:

Площади треугольников, имеющих равные высоты (общую высоту), относятся как стороны, соответствующие этим высотам.

Площади треугольников, имеющих равные стороны, относятся как соответствующе этим сторонам высоты.

Площади треугольников, имеющих равный угол (или общий угол), относятся как произведения сторон, содержащих этот угол.

Соотношение площадей фигур, связанных с трапецией:

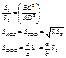
Площадь произвольного четырехугольника:

Площадь ромбоида:

Темы:

1.  Формулы сокращ. умнож. Схема Горнера.

2.  Основные приемы преобразования графиков.

3.  Тригонометрия (осн. формулы)

4.  Тригонометрия (формулы сложения и двойного угла)

5.  Тригонометрия (формулы понижения степени и универс. подстановка).

6.  Тригонометрия (формулы суммы и формула доп. угла).

7.  Тригонометрические уравнения и значения .тригонометрических функций.

8.  Логарифмы.                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                       

9.  Производная.

10.  Прогрессии.

11.  Треугольник.

12.  Параллелограмм.

13.  Трапеция.

14.  Окружность.

15.  Нахождение биссектрис, медиан и т.д.

16.  Площади.

17.  Стереометрия.

18.  Некоторые указания.

Некоторые указания:

При записи выражения для ОДЗ, для уравнений вида f(x)=g(x), берем одно любое, для неравенств вида f(x)>g(x), берем то, что меньше, т.е. g(x) (для неравенств f(x)<g(x), берем f(x))

При работе с модулем важно помнить, что модуль число не отрицательное, т.е. и

При раскрытии неравенств вида: получаем промежуток , для неравенств вида , получаем объединение промежутков: ; при решении неравенств вида: , данное равносильно

При решении систем уравнений часто используется замена: x+y=p и xy=q