Математическая постановка оптимизационных задач. Приложения дифференциального исчисления

Фирма имеет контракты на поставку кирпичей на ближайшие четыре недели в количестве 58000 шт., 36000 шт., 52000 шт. и 70000 шт. соответственно (доставка осуществляется один раз в конце недели). Из-за разницы цен на энергоносители в течение этих недель стоимость производства тысячи кирпичей меняется и составляет 840 рублей в первую неделю, 810 рублей во вторую, 780 в третью и 870 в четвертую. Из-за наличия других заказов фирма может произвести 60 тысяч кирпичей в первую неделю, 62 тысячи во вторую, 64 тысячи в третью и 66 тысяч в четвертую. Хранение произведенных неотправленных кирпичей обходится в 9 рублей за тысячу штук в неделю. При каком плане суммарные издержки производства и хранения оказываются минимальными?

Решение:

Пусть x_t – количество произведенных кирпичей, тыс. шт., а h_t – объем хранения готовой продукции также в тыс. шт. Тогда спрос на кирпичи определится следующим образом:

S_t=h_t-1+x_t-h_t

Ограничения по спросу:

x₁-h₁=58

h₁+x₂-h₂=36

h₂+x₃-h₃=52

h₃+x₄=70

Ограничения по мощности:

0£x_t£M_t

0£x₁£60

0£x₂£62

0£x₃£64

0£x₄£66

Определим затраты: f_t – суммарные затраты на производство и хранение готового кирпича на неделе t:

f₁=840x₁+9h₁

f₂=810x₂+9h₂

f₃=780x₃+9h₃

f₄=870x₄+9h₄

Тогда суммарные затраты, которые нужно минимизировать, составят:

Приложения дифференциального исчисления

15. Некто нанял пароход для перевозки грузов на расстояние 1000 км. Он предлагает хозяину парохода плату в размере 1500 золотых монет за вычетом 9 монет за каждый час нахождения в пути. За поддержание скорости  км/ч команда получает от хозяина премию в  золотых монет. При какой скорости хозяин парохода заработает больше всего золотых монет?

Решение:

Пусть скорость обозначим v.

Время в пути t=1000/v.

Оплата P=1500-9*(1000/v)-10v= 1500-9*(1000/v)-10

Найдем максимум функции: P`=9000/v²-10=0 =>v=30 км/ч

Хозяин заработает P=1500-9*1000/30-10*30=900 золотых монет

16. В гостинице 60 мест. При цене 600 рублей за место бывает занято 50 мест, а при цене 560 рублей за место оказываются занятыми 55 мест. Запишите закон спроса, считая его линейным, и зависимость выручки от цены. При какой цене достигается максимальная выручка?

Решение:

Найдем закон спроса S=I-kp:

k=(50-55)/(560-600)= 0,125

I=50+0,125*600=125

S=125-0,125p

Выручка V=pS=125p-0,125p²

Найдем максимум:

V`=125-0,25p=0

P=500

Спрос при оптимальной цене S=125-0,125*500=62,5

Это больше чем имеется в наличии. Т.к. функция выручки убывающая, следовательно, надо проверить выручку на границе интервала - 60 мест.

Цена для заполнения 60 мест составит 520 руб.

Максимальная выручка:

V=520*60=31200 руб.

17. Законы спроса и предложения имеют вид  и , где  — цена единицы товара. Постройте графики соответствующих функций и найдите точку равновесия. Определите, какую минимальную цену на этот товар может установить государство, если для покупки излишка продукции выделена сумма в 105 денежных единиц.

Решение:

Построим функции

p	10	11	12	13	14	15	16	17	18	19	20
D	11,9	11,9	11,9	11,9	12	12	12	12	12	12	12
S	0,7	2,3	4	5,7	7,3	9	10,7	12,3	14	15,7	17,3

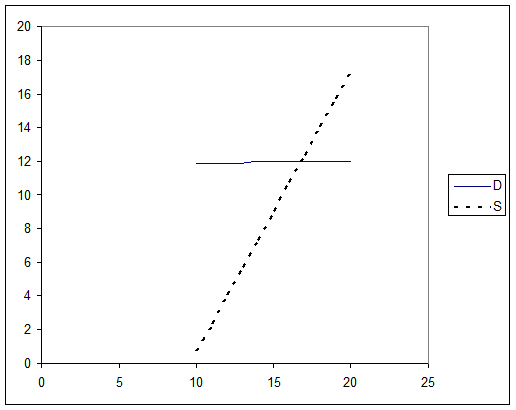
Точка равновесия:

, p₁=16,78 ед. p₂=0,02 ед. но при р=0,02 функции принимают отрицательные значения , значит этот корень не подходит.

Найдем равновесный спрос:

 ед.

Если выделено 105 единиц для покупки товара, то спрос:

Найдем функцию P(D)=, и найдем её минимум.

 и всегда меньше нуля следовательно цена убывает при росте спроса. Функция не имеет экстремума. Решения нет.

Теория вероятностей

19. В ящике для игрушек лежат три кубика, три шарика и три пирамидки. Предположим, что обезьяна взяла из ящика кубики, затем шарики, а затем пирамидки.

(1)     Найдите вероятность такого события при случайном выборе.

(2)     Можно ли на основании данного события утверждать, что обезьяна различает форму игрушек? Почему?

Решение:

1) Вероятность того, что первой игрушкой обезьяна выберет кубик, равна:

Р(А₁)=3/9=1/3

Вероятность того, что второй игрушкой обезьяна выберет кубик при условии, что первый был тоже кубик, равна:

=2/8=1/4

Вероятность того, что третьей игрушкой также будет кубик (при условии, что первые два – кубики), будет:

=1/7

Аналогично:

четвертый шарик если первые 3 кубики:

=3/6=1/2

пятый шарик, если первые 3 кубики и четвертый шарик:

=2/5

шестой шарик, если первые 3 кубики и четвертый и пятый шарики:

=1/4

После этого в ящике останутся только пирамидки, поэтому вероятность взять следующей игрушкой пирамидки будет равна 1:

=1

Поскольку все события зависимы, то вероятность произведения этих