Глава 5. Применение производных
5.1. Правило Лопиталя.
Среди неопределенных выражений чаще всего приходится встречаться с
неопределенностями типа ![]() или
или ![]() . При их раскрытии очень помогает
так называемое правило Лопиталя.
. При их раскрытии очень помогает
так называемое правило Лопиталя.
Раскрытие неопределенностей типа ![]() .
.
Теорема1. Пусть
а) функции
![]() и
и ![]() определены и непрерывны на
определены и непрерывны на ![]() ;
;
б) в
![]() существуют
существуют ![]() и
и ![]() , причем
, причем ![]() ;
;
в) ![]() ;
;
г) ![]() .
.
Тогда ![]() .
.
Доказательство.
В точке а функции ![]() и
и ![]() не определены. Доопределим их
по непрерывности, полагая
не определены. Доопределим их
по непрерывности, полагая ![]() .
Тогда по формуле Коши
.
Тогда по формуле Коши
![]() , где
, где ![]() . Поэтому при
. Поэтому при ![]() также будет
также будет ![]() . Переходя к пределу, получим
. Переходя к пределу, получим
![]() , так как
последний предел существует. <
, так как
последний предел существует. <
Теорема2.
Пусть
а) функции![]() и
и ![]() определены и непрерывны на
определены и непрерывны на ![]() ;
;
б) в
![]() существуют
существуют ![]() и
и ![]() , причем
, причем ![]() ;
;
в) ![]() ;
;
г) ![]() .
.
Тогда ![]() .
.
Доказательство.Сделаем «замену переменной» ![]() . Тогда при
. Тогда при ![]()
![]() и мы можем воспользоваться
предыдущей теоремой. Имеем
и мы можем воспользоваться
предыдущей теоремой. Имеем
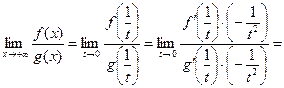
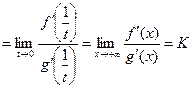 , что
и доказывает теорему. <
, что
и доказывает теорему. <
Несмотря на свою внешнюю простоту, правило Лопиталя довольно сложно при его практическом использовании. При практическом применении этого правила следует иметь в виду следующие рекомендации:
а) прежде, чем находить ![]() рекомендуется выражение
рекомендуется выражение ![]() упрощать,
насколько это возможно;
упрощать,
насколько это возможно;
б) если при вычислении ![]() снова подучилась неопределенность, то применить правило
Лопиталя еще раз. Однако перед его повторным применением рекомендуется выделить
отдельно сомножители, не стремящиеся к нулю, и заменить их предельными
значениями.
снова подучилась неопределенность, то применить правило
Лопиталя еще раз. Однако перед его повторным применением рекомендуется выделить
отдельно сомножители, не стремящиеся к нулю, и заменить их предельными
значениями.
Рассмотрим два примера на эти рекомендации.
Пример 1.
Вычислить ![]() .
.
Решение. Используем правило Лопиталя. Имеем
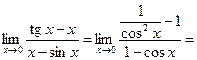
И вот тут не имеет смысла сразу подставлять ![]() , так как снова получилась неопределенность.
Не имеет также смысла сразу применять правило Лопиталя еще раз - залезем в такие дебри, из
которых не выберемся. Поэтому сначала упрощаем - убираем «трехэтажность» и
сокращаем сомножитель
, так как снова получилась неопределенность.
Не имеет также смысла сразу применять правило Лопиталя еще раз - залезем в такие дебри, из
которых не выберемся. Поэтому сначала упрощаем - убираем «трехэтажность» и
сокращаем сомножитель ![]() :
:
![]()
И вот тут уже можно смело подставить ![]() , так как нет никакой
неопределенности:
, так как нет никакой
неопределенности:
=2.
Пример 2.
Вычислить ![]() .
.
Решение. Используем правило Лопиталя и упрощаем. Имеем
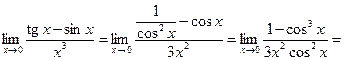
У нас снова получилась неопределенность. Но, прежде чем применять правило Лопиталя еще раз, надо сначала выделить сомножители, не стремящиеся к 0, и вычислить их предел отдельно:
![]()
А вот теперь к оставшемуся выражению применяем правило Лопиталя
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.