Глава 3. Непрерывные функции
3.1 Определения.
Дадим несколько расшифровок этого важнейшего определения. а) Вспоминая понятие предела, запишем непрерывность f(x) в точке х0 в виде
![]() .
.
б) Так как ![]() , то непрерывность в
точке х0 можно записать в виде
, то непрерывность в
точке х0 можно записать в виде
![]() .
.
Отсюда следует важнейшее свойство непрерывной функции: для непрерывной функции можно переставлять местами знак функции и знак предельного перехода
![]()
в) Обозначим Dx=x-x0 (приращение аргумента) и Df=f(x) - f(x0) (приращение функции). Тогда непрерывность в точке х0
означает, что ![]() , то есть
бесконечно-малому приращению аргумента соответствует бесконечно-малое
приращение функции.
, то есть
бесконечно-малому приращению аргумента соответствует бесконечно-малое
приращение функции.
Ведем обозначения:
![]() , если эти пределы существуют.
, если эти пределы существуют.
Определение 2. Функция f(x) называется непрерывной в точке х0 слева (справа) если f(x0)=f(x0 – 0) (f(x0)=f(x0+0)). Очевидно, что непрерывность в точке х0 означает непрерывность слева и справа одновременно.
Определение 3. Функция f(x) называется непрерывной на некотором множестве Х, если она непрерывна в каждой точке этого множества, то есть если
![]()
Обратите внимание, где стоит квантор ![]() , это важно.
, это важно.
Определение. Если функция f(x) не является непрерывной в точке х0, то говорят, что в точке х0 функция f(x) имеет разрыв.
3.2 Типы разрывов.
|
|
А. Пусть существуют конечные f(x0-0) и f(x0+0), они равны друг другу, но не равны значению функции в точке х0, то есть выполнено условие f(x0-0) = f(x0+0) ≠ f(x0), то говорят, что в точке х0 функция f(x) имеет устранимый разрыв. Действительно, достаточно изменить значение функции в точке х0 и разрыв исчезнет. Вид графика функции в этом случае приведен на рисунке. |
В. Пусть существуют конечные f(x0-0) и f(x0+0), но они не равны друг другу ![]() . Тогда говорят, что в точке х0
функция f(x) имеет разрыв I
рода или скачок.
. Тогда говорят, что в точке х0
функция f(x) имеет разрыв I
рода или скачок.
График функции f(x) в окрестности точки х0 имеет в этом случае примерно такой вид:
|
|
|
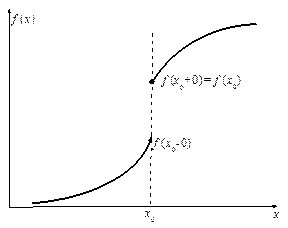
![]()
Величина |f(x0+0)-f(x0-0)| называется величиной скачка функции f(x) в точке х0.
В. Если хотя бы один из пределов ![]() или
или ![]() бесконечен
или не существует, то говорят, что в точке х0 функция f(x)
имеет разрыв второго рода.
бесконечен
или не существует, то говорят, что в точке х0 функция f(x)
имеет разрыв второго рода.
Виды графика функции f(x) в окрестности точки х0 в этом случае гораздо разнообразнее. Некоторые возможные варианты приведены ниже.
|
|
|
|
|
не существуют. |
3.3 Свойства непрерывных функций. Непрерывность сложной функции.
Доказательство.
Пусть f(x) и g(x) непрерывны в точке x0. Это значит, что ![]() . Но тогда, по свойствам пределов
. Но тогда, по свойствам пределов
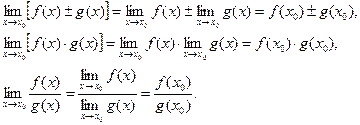
Последнее свойство верно, если ![]() . <
. <
Пусть y=f(x), но x, в свою очередь, является функцией некоторого аргумента t: x=j(t). Тогда комбинация y=f(j(t)) называется сложной функцией, или суперпозицией функций f(x) и j(t).
Примеры:
а) y=sin(x), x=et Þ y=sin(et)
б) y= ex , x=sin(t) Þ y= esin(t)
Теорема о непрерывности сложной функции.
Пусть функция j(t) непрерывна в точке t0 и функция f(x) непрерывна в точке х0=j(t0). Тогда функция f(j(t)) непрерывна в точке t0.
Доказательство.
Для доказательства этой теоремы воспользуемся формальным преобразованием двух строчек кванторов. Имеем
![]() непрерывна в точке
непрерывна в точке ![]() ,
,
![]() непрерывна в точке
непрерывна в точке ![]() , или
, или ![]() .
.
Выписывая подчеркнутые кванторы, получим, что
![]() , что и говорит о том, что f(j(t)) непрерывна в точке t0. <
, что и говорит о том, что f(j(t)) непрерывна в точке t0. <
Обратите внимание на следующие детали:
а) так как x=j(t), то |j(t)-j(t0)|<d может быть записано
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.