ГЛАВА 1. Множества. Вещественные числа
1.1 Множества
Понятие множества является первоначальным математическим понятием, то есть таким понятием, которое можно только показать на примерах. Можно говорить, например, о множестве людей, находящихся в данной аудитории, о множестве четных чисел, о множестве точек отрезка и т.п. Множества мы будем в дальнейшем обозначать большими латинскими буквами, например, A, B,C и т.д. Иногда множества будут задаваться просто перечислением их элементов и для этого будет использоваться запись вида A={a}, где в {…} будут перечисляться элементы множества A. Например, A={a, b, c} есть множество, состоящее из элементов a, b и c.
Обозначение aÎA означает, что элемент a принадлежит множеству A,
а обозначение ![]() или aÏA означает, что элемент aне принадлежит множеству A. Знаком Æ будет обозначаться так
называемое пустое множество, то есть такое множество, в котором нет ни
одного элемента.
или aÏA означает, что элемент aне принадлежит множеству A. Знаком Æ будет обозначаться так
называемое пустое множество, то есть такое множество, в котором нет ни
одного элемента.
1.2 Операции над множествами
1. Вхождение или включение множеств.
Говорят, что множество А входит
во множество В (обозначение АÌВ) или множество В включает
множество А (обозначение ВÉА) если из того, что некоторый
элемент aÎA следует, что aÎВ (запись ![]() ).
).
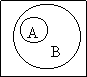 Эту операцию можно
пояснить следующим рисунком. Из него видно, что если АÌВ, то множество В
шире множества А, то есть содержит бóльшее число элементов.
Эту операцию можно
пояснить следующим рисунком. Из него видно, что если АÌВ, то множество В
шире множества А, то есть содержит бóльшее число элементов.
Если одновременно АÌВ и ВÌА, то означает, что множества А и В совпадают, или равны друг другу (обозначение А=В).
2. Объединение или сумма множеств.
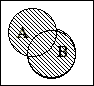 Множество С
называют объединением или сумой множеств А и В
(обозначение С=АÈВ) если оно состоит из элементов,
принадлежащих хотя бы одному из множеств А и В, то есть aÎС означает, что aÎA, или aÎВ или aÎ и А и В
одновременно. Это можно записать так:
Множество С
называют объединением или сумой множеств А и В
(обозначение С=АÈВ) если оно состоит из элементов,
принадлежащих хотя бы одному из множеств А и В, то есть aÎС означает, что aÎA, или aÎВ или aÎ и А и В
одновременно. Это можно записать так: ![]() ,
где знак Ú есть символ логического сложения (читается
«или»). Эта операция может быть пояснена следующим рисунком.
,
где знак Ú есть символ логического сложения (читается
«или»). Эта операция может быть пояснена следующим рисунком.
Операция È обладает обычными свойствами:
1) АÈВ= ВÈА;
2) АÈ( ВÈС)=(АÈВ) ÈС.
Для суммы множеств А1,
А2,…, Аn используют обозначение ![]() .
.
3. Пересечение или произведение множеств.
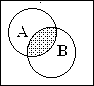 Множество С
называется пересечением или произведением множеств А и В
(обозначается С=АÇВ) если оно состоит из элементов,
принадлежащих одновременно и множеству А и множеству В.
Это можно записать так:
Множество С
называется пересечением или произведением множеств А и В
(обозначается С=АÇВ) если оно состоит из элементов,
принадлежащих одновременно и множеству А и множеству В.
Это можно записать так: ![]() где знак Ù есть символ
логического умножения (читается «и»). Эта операция может быть пояснена
следующим рисунком.
где знак Ù есть символ
логического умножения (читается «и»). Эта операция может быть пояснена
следующим рисунком.
Операция Ç обладает свойствами:
1) АÇВ= ВÇА;
2) АÇ( ВÇС)=(АÇВ) ÇС.
По отношению друг к другу операции Ç и È обладают следующими свойствами:
1). (АÈВ) ÇС=(АÇС) È(ВÇС)
(сравните с обычным соотношением из алгебры (a+b)c=ac+bc)
2). (АÇВ)ÈС=(АÈС) Ç(ВÈС)
Для пересечения множеств А1,
А2,…Аn используют символ ![]() .
.
4. Вычитание или разность множеств.
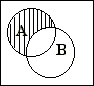 Множество С
называется разностью множеств А и В (обозначается С=А\В),
если оно состоит из элементов, принадлежащих А, но не принадлежащих В.
(Это можно записать так:
Множество С
называется разностью множеств А и В (обозначается С=А\В),
если оно состоит из элементов, принадлежащих А, но не принадлежащих В.
(Это можно записать так: ![]() ). Данный
рисунок поясняет эту операцию.
). Данный
рисунок поясняет эту операцию.
В дальнейшем нам наиболее часто придется иметь дело с двумя множествами.
N={1, 2, 3, 4, ... } – множество всех целых положительных чисел и
Z={0, +1, -1, +2, -2, +3, -3, +4, -4, ... } – множество всех целых чисел.
1.3 Сравнение множеств по числу элементов.
Пусть даны два множества: А={a, b, c} и B={a, b, g}. Спрашивается: в каком множестве больше элементов. Или даны два множества А={a, b, c} и С={1, 2, 3, 4}. Где больше элементов?
Видимо, на этот вопрос ответят все и на дополнительный вопрос: «А как Вы это узнали?» также ответят просто: сосчитали. В множестве А 3 элемента, в множестве В – тоже 3, в множестве С – 4, так что ответ очевиден.
Но вот более сложный вопрос: даны два множества N={1, 2, 3, 4, …} и D={2, 4, 6, 8,…}. В каком множестве больше элементов? И на сам собой напрашивающийся ответ: «конечно, их больше в N. Больше в 2 раза» можно спросить: «А как Вы это узнали? Неужели сосчитали? Но ведь в этих множествах бесконечное число элементов, так что сосчитать Вы никак не могли».
Или: даны 2 отрезка - AB и CD:
На каком отрезке больше точек? И на ответ «Конечно, на CD, ведь
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.