5. Приложения преобразования Фурье

1
5. Приложения преобразования Фурье
5.1. Предсказание высоты прилива.
5.2. Интерполяция рядами Фурье.
5.3. Фурье-анализ в акустике.
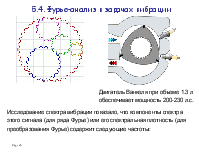
5.4. Фурье-анализ в задачах вибрации.
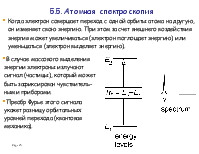
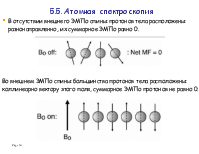
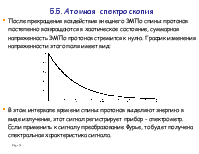
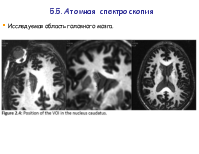
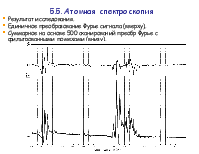
5.5. Атомная спектроскопия.

2
5. Приложения преобразования Фурье
-
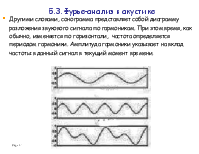
Монотонное постукивание колес поезда (звук) – периодическая функция. Бег спортсмена, вращение Земли, биение сердца – все это можно выразить периодические функциями от времени. Каждая из этих функций представима рядом Фурье, суммой синусоид и косинусоид – как их называют, гармоник. Если брать только аргументы этих тригонометрических функций, то получим спектр периодической функции. Представление периодических функций рядом Фурье и их преобразование для анализа частотных свойств оказалось очень полезным.
Page 3
5.1. Предсказание высоты прилива
-
Так, в конце XIX века лорд Кельвин на основе разложения в ряд Фурье построил аналоговое вычислительное устройство, которое позволяло оценивать высоту приливов. Вначале в конкретной гавани на протяжении года измеряли уровень моря и записывали соответствующие положения Солнца и Луны. По этим записям определяли параметры аналогового механического вычислителя, который выдавал приливные высоты в гавани как функцию от времени.
-
Выбор метода оказался удачным, таблицы высоты приливов были составлены для всех портов мира.
Page 4
5.1. Предсказание высоты прилива

Аналоговый показатель приливов Феррела (усовершенствованная машина Кельвина).
Вид сзади: устанавливались параметры вычислений. Вид спереди: результат – показывает верхний и нижний уровни прилива.
Page 5
5.2. Интерполяция рядами Фурье
-
Интерполирование – это приближенное или точное нахождение какой-либо величины по известным отдельным значениям этой же или связанной с ней другой величиной. Проще говоря – это восстановление значений функции в точке, значение в которой неизвестно, по ее известным значениям в других точках.
-
Ряд Фурье можно применять для интерполяции, но интерполяция рядом Фурье строит приближенную функцию, которая не обязательно проходит по заданным точкам.
-
Рассмотрим пример.
Page 6
5.2. Интерполяция рядами Фурье
-
Пример. Интерполирование в декартовой системе координат.
-
Пусть задано 10 точек на плоскости, никакие две из которых не лежат на одной вертикальной прямой. Требуется построить гладкую кривую, проходящую «близко» от этих точек.
-
Множество точек P:
-
{0.00, 2.18}, {1.22, 2.48}, {1.89, 2.52},
-
{2.55, 2.32}, {3.19, 2.34}, {3.71, 1.79},
-
{5.42, 1.78}, {5.06, 1.45}, {5.65, 2.20},
-
{6.28, 2.18}
-
– это координаты {xi,yi } , i=1,…,10.
Page 7
5.2. Интерполяция рядами Фурье
-
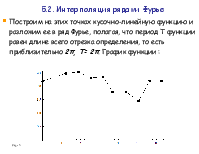
Построим на этих точках кусочно-линейную функцию и разложим ее в ряд Фурье, полагая, что период Т функции равен длине всего отрезка определения, то есть приблизительно 2π, Т= 2π. График функции :
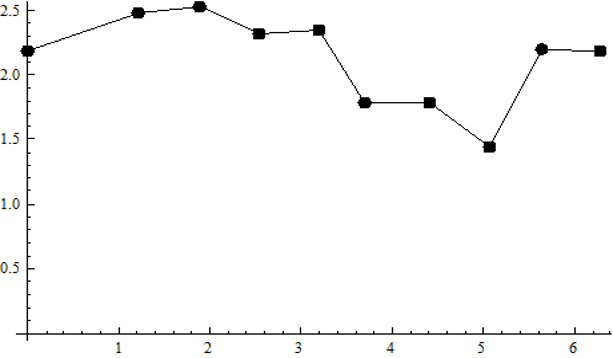
Page 8
5.2. Интерполяция рядами Фурье
-
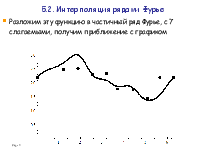
Разложим эту функцию в частичный ряд Фурье, с 7 слагаемыми, получим приближение с графиком
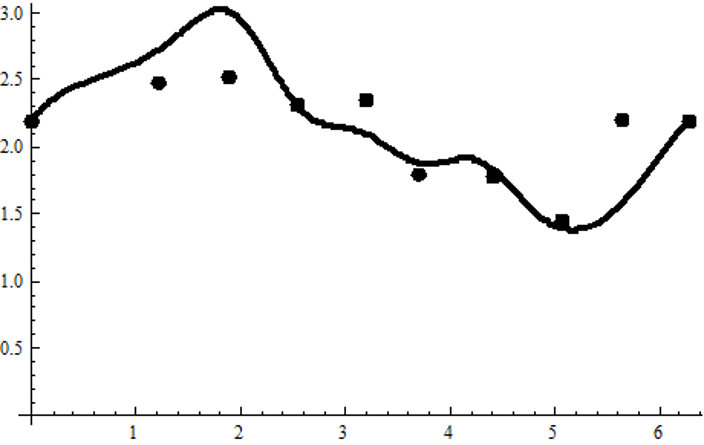
Page 9
5.2. Интерполяция рядами Фурье
-
Если рассмотреть этот результат в полярных координатах, то и там интерполяция будет не лучше. Рассматривая xi как угол θi, а yi как радиус ri, получаем график
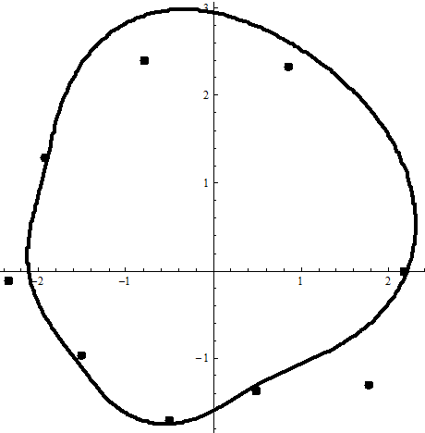
Page 10
5.2. Интерполяция рядами Фурье
-
При этом коэффициенты разложения быстро убывают с увеличением индекса, что означает, что ряд Фурье скорее всего сходится. Получено разложение (7 слагаемых, 6 значащих цифр в каждом) : y(x) =
-
2.16076 –
-
-0.0379978 Cos[x] +0.640706 Sin[x] -
-
-0.0768362 Cos[2 x] +0.111259 Sin[2 x] +
-
+0.138096 Cos[3 x] -0.0311125 Sin[3 x] +
-
+0.0527770 Cos[4 x] +0.0193192 Sin[4 x] -
-
- 0.0501658 Cos[5 x] +0.0035071 Sin[5 x] +
-
+0.0244504 Cos[6 x] -0.00192247 Sin[6 x]
Page 11
5.2. Интерполяция рядами Фурье
-
Увеличение числа слагаемых до 50 не дает улучшения результата. График этого разложения :
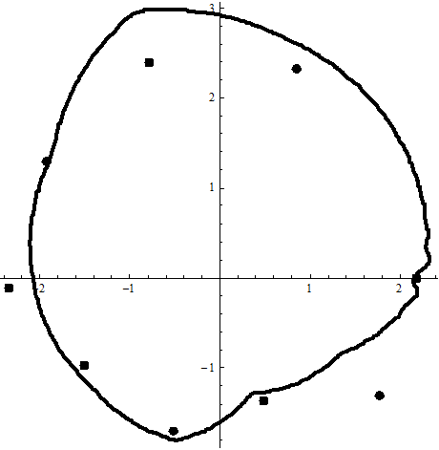
Page 12
5.3. Фурье-анализ в акустике
-
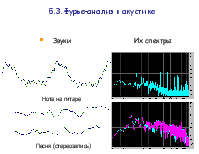
Ухо человека слышит звук, который представляет собой сигнал во временной области. Этот сигнал представлен незначительными уплотнениями и разряжением упругой среды, состоящей из молекул воздуха. Упругость среды определяется силами притяжения и отталкивания молекул. Амплитуда – громкость звука обусловлена изменением плотности воздушной массы от внешнего воздействия. У тех, кто слышит более тихие звуки (амплитуда), ухо реагирует на более слабое изменение плотности воздуха. Высота звука соответствует скорости изменения плотности (частота колебаний).
Page 13
5.3. Фурье-анализ в акустике
-
У пассажиров самолета, набирающего высоту, уши чувствуют изменение