Задачи диагностики. Отображение интервалов. Задача диагностики для b-схемы, страница 3

Выявление квазиэквивалентности произвольной пары операторов сводится к нахождению такой перестановки строк и столбцов матрицы одного из операторов, при которой эта матрица становится равной матрице другого оператора. Это нетривиальпая комбинаторная задача, на которой мы не будем здесь останавливаться. Заметим лишь, что она в сильной степени аналогична известной задаче об установлении изоморфизма графов.

Перестановочный оператор представляет собой частный случай кодирующих опeратoров, осуществляющих преобразование «без потери информации», когда различным значениям входного булева вектора х ставятся в соответствие различные значения выходного булева вектора у. Для оператора такого типа всегда можно найти обратный оператор, т. е. оператор, осуществляющий обратное преобразование значений вектора у в соответствующие им значения вектора х.

Справедливо следующее утверждение: необходимым и достаточным условием того, чтобы некоторый оператор В^V размером т на п был кодирующим оператором, является наличие в матрице В перестановочного минора размером n на n (отсюда следует, что т должно быть не меньше n).

Достаточность этого условия очевидна: если условие выполняется, то каждой входной булевой переменной x_i ставится в соответствие некоторая выходная переменная y_i совпадающая по значению с x_i. Необходимость доказывается рассуждением от противного: если перестановочного минора в матрице В нет, то это означает, что в матрице отсутствует строка с единственной единицей в некоторой i-й компоненте, а отсюда в свою очередь следует, что два значения входного вектора х, одно из которых состоит сплошь из единиц, а другое содержит единственный нуль в i-й компоненте, не смогут отобразиться в различные значения вектора у.

Если оператор В^V является кодирующим, то обратное преобразование вектора у в вектор х осуществляется оператором С^V, матрица которого получается из матрицы В путем замены 1 на 0 во всех строках, не входящих в перестановочный минор, и транспонирования получаемого при этом результата.

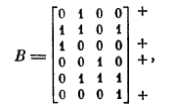
Например, если

то оператор В^V является кодирующим, поскольку отмеченные знаком + его строки образуют перестановочный минор. Поэтому существует обратное преобразование вектора у в вектор х, реализуемое оператором С^V   с матрицей

Заметим, что обратное преобразование не является кодирующим в полном смысле этого слова, поскольку различные значения вектора у могут отображаться одинаковыми значениями вектора x. Ho оно является кодирующим для множества всех тех значений вектора у, которые могут появиться на выходе матричной схемы, описываемой кодирующим оператором В^V.

Отображение интервалов. Полное описание отображения множества М значений входного булева вектора х в множество N значений выходного булева вектора у связано с перечислением всех пар значений этих векторов. Однако в некоторых ситуациях достаточно знать такую грубую, но довольно важную характеристику рассматриваемого матричного оператора, как создаваемый им образ булева пространства М в пространстве N. Этот образ может быть представлен характеристической функцией вектора у, принимающей значение 1 на тех элементах пространства N, которые принадлежат образу, и значение 0 на остальных элементах из N.

В других случаях более практичным оказывается описание такого уровня сложности, при котором множество М разбивается на интервалы и показывается, в какие интервалы пространства N они отображаются. Такой подход применяется, в частности, в методе «троичного моделирования», где рассматриваются троичные значения входного вектора х (значения некоторых компонент считаются неизвестными или безразличными) и находятся соответствующиеим, также троичные, значения выходного вектора у.