Задачи диагностики. Отображение интервалов. Задача диагностики для b-схемы, страница 2

Допустим, что в уравнении Y == В^VХ или У = Т^ÑХ задан лишь матричный оператор В^V или T^Ñ, а матрицы Z и У играют роль неизвестных величин. Какие содержательные задачи могут быть поставлены в этой ситуации?

Очевидно, что эти задачи должны быть каким-то образом связаны с исследованием свойств заданного матричного оператора. Рассмотрим в связи с этим некоторые характеристики операторов типа В^V и T^Ñ, а также некоторые отношения между различными операторами. Очевидно также, что сравнение однотипных операторов будет сводиться к сравнению их матриц.

Сравнение матричных операторов. Положим, что два однотипных оператора тождественны, или равны, если равны их матрицы. В свою очередь равенство матриц означает их поэлементное совпадение:

В = С, если b_i^j =c_i^j, и Т = U, если t_i^j = u_i^j, где i и j принимают любые допустимые значения из заданного диапазона, определяемого размерами сравниваемых матриц. Разумеется, размеры матриц должны также совпадать.

Два матричных оператора будем считать эквивалентными, если тождественны реализуемые ими отображения входного булева вектора х в выходной булев вектор у. Например, оператор В^V эквивалентен оператору С^V, если для любого х выполняется отношение равенства В^Vх = С^Vх, оператор Т^Ñ эквивалентен оператору U^Ñ, если выполняется отношение Т^Ñх = U^Ñх, оператор B^V эквивалентен оператору Т^Ñ, если выполняется отношение B^Vx=Т^Ñx (последний пример показывает, что эквивалентными могут быть и разнотипные операторы).

Введем также отношение ограниченной эквивалентности, или эквивалентности на матрице X, считая, например, что операторы В^V и С^V эквивалентны на X, если для любого столбца х^j матрицы Х выполняется отношение В^Vх^j == С^Vx^j.

Легко показать, что операторы b^V и С^V эквивалентны в том и только том случае, когда они равны. Аналогично операторы Т^Ñ и U^Ñ эквивалентны также в том и только том случае, когда они равны. Разнотипные операторы В^V и Т^Ñ эквивалентны в том и только том случае, когда матрица Т не содержит нулей и может быть получена из матрицы В заменой всех нулей на символ «—».

Ограниченная эквивалентность может иметь место и для неравных операторов. Именно в связи с этим и получает смысл рассмотренная выше задача минимизации числа единиц в матрице оператора В^V, реализующего заданное преобразование входной матрицы Х в выходную матрицу Y.

Обобщая понятие эквивалентности, введем отношение квазиэквивалентности, считая, что два оператора квазиэквивалентны, если они становятся эквивалентными при некоторой перестановке входных или выходных булевых переменных. Перестановку, т. е. перенумерацию переменных удобно рассматривать как действие перестановочного оператора Р^V, у которого матрица Р является квадратной булевой матрицей, содержащей ровно по одной единице в каждой строке и в каждом столбце. Очевидно, что для любой перестановки можно найти обратную перестановку, причем матрица обратной перестановки будет транспонированной формой матрицы прямой перестановки. Другими словами, для любой перестановочной матрицы Р будет выполняться отношение Р X Р^T = Е. Матрицу-единицу Е можно рассматривать как вырожденный оператор перестановки, задающий перестановку в себя.

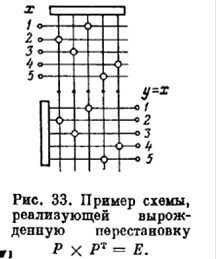
Например (см. рис. 33, обратив внимание на совпадение расположения транзисторов во входной (графически транспонированной!) и выходной транзисторных матрицах):

(изображённая схема осуществляет тождественное преобразование y=х).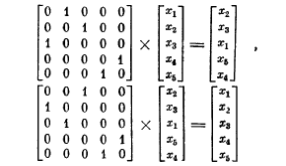

Таким образом, операторы В^V и СV квазиэквивалентны, если существует такая пара перестановочных операторов Р₁^V и Р₂^V,  что для любого значения входного вектора х будет выполняться B^vx =P₂^VC^VP₁^Vx. Аналогично определяется квазиэквивалентность троичных матричных операторов.