Сжатие булевой матрицы. Методы сканирования булева пространства

интервал содержит много элементов, то лучше свести данную задачу к уже рассмотренной нами задаче о вырожденности троичной матрицы. Делается это так: из матрицы B выделяется минор, образованный пересечением строк, неортогональных вектору u, со столбцами, в которых вектор u имеет значение «-», а затем проверяется, не является ли этот минор вырожденным. Если минор вырожден, то интервал u содержится в М¹, в противном случае не содержится. Пусть, например,

Проверим первый из перечисленных в матрице В элементов множества М¹ - строку 1. Сравнивая ее с другими строками, выявляем соседей

101111  4

000111  6

и строим определяемый ими минимальный поглощающий интервал

- 0 - 1 1 1

Этот интервал задает в матрице В минор вырожденность которого легко устанавливается. Отсюда следует, что элемент 100111 является определяющим, а определяемый им интервал - 0 - 1 1 1 является обязательным.

Вычисления можно значительно упростить, если элемент а имеет мало соседей. В частности, если у него нет соседей, то он сам образует обязательный интервал. Если он обладает лишь одним соседом, то обязательный интервал образуется склеиванием элемента а с этим соседом. Если элемент а имеет двух соседей, один из которых ортогонален ему по компоненте i, а другой — по компоненте j, то вычисления сводятся к проверке наличия в множестве М¹ элемента, ортогонального элементу а по двум компонентам i и j. В случае трех соседей достаточно найти в множестве М¹ элемент, ортогональный элементу а по трем соответствующим компонентам, и убедиться в том, что вместе с этим элементом множество М¹ содержит и его соседей по данным компонентам.

Рассмотрим попутно следующую задачу. Допустим, что мы получили каким-то образом интервал u множества М¹ и желаем узнать, является ли он обязательным. Из предыдущих рассуждений следует, что он обязателен, если какой-либо из его элементов является определяющим. Определяющий элемент можно назвать также внутренним элементом определяемого им интервала, имея в виду, что все его соседи, принадлежащие множеству М¹, также принадлежат интервалу. Остальные элементы интервала, не обладающие данным свойством, присущим внутреннему элементу, естественно назвать граничными.

Таким образом, интервал u множества М¹ обязателен, если он имеет внутренние элементы. Для того чтобы узнать, есть ли у него внутренние элементы, нет необходимости испытывать по очереди все его элементы. Можно решить эту задачу иначе.

Выделим из матрицы В минор, образуемый пересечением строк, смежных с интервалом u (т. е. не принадлежащих этому интервалу, но соседних с некоторыми его элементами), и столбцов, в которых вектор u имеет значение «—». Затем определим, является ли этот минор вырожденным. Если минор вырожден, то это означает, что для каждого элемента интервала u в множестве М¹ найдется соседний с ним элемент, не принадлежащий интервалу u, откуда следует, что интервал u не обязателен. Если же минор не вырожден, т. е. если существует некоторый булев вектор, ортогональный каждой строке минора, то задаваемый этим вектором элемент интервала u не будет иметь в множестве М¹ соседей, не принадлежащих интервалу u. В этом случае интервал u обязателен.

Допустим, что, рассматривая некоторую булеву матрицу В, задающую множество М¹, мы нашли некоторый интервал u этого множества

- 0 - 1 1 -

и выделили в матрице В следующие строки, смежные с u:

110111

        101010

 000100

    010110

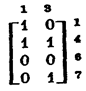
Выбирая столбцы, в которых вектор u имеет значение «—», мы строим из них минор

 

 1 0 1

 1 1 0

 0 0 0

 0 0 0

и легко устанавливаем его невырожденность, означающую, что интервал u обязателен. Например, ортогональным этому минору оказывается вектор 111. Задаваемый этим вектором элемент 101111 интервала u не имеет, следовательно, соседей в множестве М¹, которые не принадлежали бы данному интервалу, т. е. этот элемент является внутренним элементом интервала u.

Допустимые  интервалы   как  элементы кратчайшего покрытия. Найдя в множестве М¹ хотя бы один обязательный интервал, мы можем открыть дорогу цепному процессу конструирования элементов покрытия этого множества, который при благоприятных обстоятельствах может завершиться получением точного решения интересующей нас задачи.

Рассмотрим текущую ситуацию, когда часть элементов множества М¹ оказывается уже покрытой некоторыми интервалами, выбор которых был строго обоснован, а другая часть, образующая текущее, т. е. изменяемое в процессе решения множество М*, состоит из тех элементов множества М¹, которые не принадлежат ни одному из выбранных интервалов. Именно об их покрытии и следует далее беспокоиться.