






и Y, представляющая некоторую систему булевых функций: если некоторые два столбца матрицы У находятся в отношении ортогональности, то соответствующие им два столбца матрицы Х также должны быть взаимно ортогональными. Очевидно, что это условие будет всегда выполняться, если все столбцы матрицы Х взаимно ортогональны, в частности, если мы используем булеву матрицу Х с попарно различными столбцами.
Для дальнейшего изложения нам понадобится еще одна форма представления системы булевых функций. Точнее говоря, эта форма представляет систему ДНФ. Она состоит из троичной матрицы X, задающей своими столбцами некоторую систему интервалов и соответствующих им элементарных конъюнкций, и булевой матрицы Y, интерпретируемой теперь следующим образом: если уji = 1, то j-я элементарная конъюнкция, представляемая 7-м столбцом матрицы X, входит в i-ю дизъюнктивную нормальную форму, представляемую i-ц строкой матрицы У. Примером может служить пара матриц
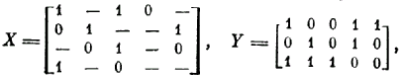 |
С вводом значения «—» мы перешли, по существу, к рассмотрению троичных переменных. Подготавливая почву для дальнейшего изложения, введем серию операций над троичными переменными, определив их как такое обобщение соответствующих булевых операций, при котором значение «—» интерпретируется как символ неопределенности двоичного значения, т. е. считается, что рассматриваемая переменная принимает одно из двух значений, О или 1, но какое именно, неизвестно.
 |
Например, рассматривая дизъюнкцию р \/ q, мы полагаем, что эта функция принимает значение 1, если известно, что по крайней мере одна из переменных р и q обладает значением 1, принимает значение 0, если известно, что обе переменные имеют значение 0, и принимает значение «—», т. е. остается неопределенной, во всех остальных случаях.
Нетрудно убедиться, что сохраняется старая интерпретация дизъюнкции и конъюнкции:
![]()
(при этом надо считать, что 0 < — < 1). Сохраняются также
остальные свойства всех операций и отношения между ними.
ГЛАВА 2 МЕТОДЫ КОМБИНАТОРНОГО ПОИСКА
5. Комбинаторный поиск
Полный перебор. Традиционная математика приучила нас к аналитическим процессам решения различных задач, представляющим собой целенаправленные вычислительные процедуры, непосредственно ведущие к цели. Комбинаторные аспекты остаются при этом в тени. Однако при решении логических задач комбинаторика выходит явно на первый план, становится очевидной и неизбежной. Процесс поиска решения приобретает комбинаторный характер.
В своей простейшей, тривиальной форме комбинаторный поиск сводится к так называемому полному перебору конструкций некоторого типа, среди которых, как нам заранее известно, должно находиться и решение рассматриваемой задачи. Перебираемые конструкции по очереди испытываются, и как только выясняется, что очередная из них является решением, процесс решения задачи может считаться завершенным.
В некоторых случаях этот простой метод может оказаться единственно возможным, особенно в специально созданных ситуациях. Пусть, например, нам требуется открыть секретный замок, зная лишь, что ключом к нему служит некоторое пятизначное десятичное число, а какое именно — неизвестно. Очевидна неизбежность перебора, объем которого может достигать 100 000 перебираемых элементов (лишь в этом случае решение гарантируется).
Логические задачи замечательны тем, что то множество, среди элементов которого ищется решение, всегда конечно, и, реализовав полный перебор элементов множества, мы всегда найдем решение или убедимся в том, что рассматриваемая задача вообще не имеет решений. Поэтому любая логическая задача может быть решена «в принципе», т. е. конечной решающей процедурой. Однако это не означает, что она может быть решена практически, за приемлемое время, даже с помощью самой быстро-действующей ЭВМ.
Допустим, что, решая некоторую задачу, мы знаем, что ее решение представляется неизвестной нам булевой функцией от восьми переменных. Можно ли надеяться на успех, применив здесь метод полного перебора?
Известно, что число различных булевых функций от т
переменных равно 2 в степени 2m , т. е. при т = 8 равно 2256> 1085. Это очень большое число, и перебрать столько элементов практически невозможно. Чтобы убедиться в этом, достаточно вспомнить, что число элементарных частиц во Вселенной не превышает 1079 (по Эддингтону), или подсчитать, что сверхбыстродействующая ЭВМ, выполняющая за одну секунду 100 000 000 операций, успела бы выполнить за все время существования нашей Галактики (десятки миллиардов лет) не более чем 1026 элементарных операций.
Становится очевидным, что метод полного перебора применим разве что в самых простых ситуациях. В общем же случае поиск решения должен быть сопряжен с существенным сокращением объема перебора, возможным лишь на основе учета дополнительной информации о решаемой задаче и свойствах ее решений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.