Методы комбинаторного поиска. Дерево поиска без повторения ситуаций, страница 2

Дерево поиска. Один из наиболее общих и плодотворных подходов к решению самых разнообразных логических задач заключается в построении многошаговых ветвящихся процессов, реализующих режим поиска решения с ветвлением вариантов, их оценкой, выбором перспективных продолжений решающего процесса, захождением в некоторые тупики и отбрасыванием соответствующих ветвей, после чего приходится возвращаться к старым ситуациям, с тем чтобы рассмотреть другие вытекающие из них варианты, и т. д.

Общая схема такого процесса может быть представлена деревом поиска, которое определяется следующим образом. Корень дерева поиска ставится в соответствие с исходной ситуацией, остальные вершины — с ситуациями, которых можно достичь в процессе поиска. Дуги соответствуют некоторым достаточно простым операциям — шагам решающего процесса — и связывают вершины, со

ответствующие ситуациям, одна из которых преобразуется в другую посредством одного шага. Решения рассматриваемой задачи могут представляться некоторыми вершинами этого дерева или путями. Иногда требуется найти все решения, иногда лишь одно из них, неважно какое именно, а иногда — оптимальное в определенном смысле, например представленное кратчайшим путем.

Важно отметить, что дерево поиска обычно не задается априори, а строится уже в процессе поиска: когда возникает некоторая ситуация, тогда и определяются возможные продолжения процесса, представляемые совокупностью дуг, исходящих из вершины, соответствующей данной ситуации. Естественно стремиться по возможности сократить число этих дуг, чтобы быстрее найти решение. Способы этого сокращения строятся с учетом особенностей конкретных задач.

Проиллюстрируем этот общий подход на следующем примере.

Как отмерить ровно 6 л воды, пользуясь водопроводным краном и двумя кувшинами, первый из которых обладает емкостью 5 л, второй — 7 л?

Представим текущую ситуацию вектором (р, q), где р — количество воды в первом сосуде, q —количество воды во втором сосуде, и примем за начальную ту ситуацию, когда оба кувшина пусты, т. е. ситуацию, представляемую значением (0, 0) вектора (р, q), или, короче, значением О О. В каждой ситуации возможны следующие операции:

а) долить первый кувшин, б) долить второй кувшин, в) вылить воду из первого кувшина, г) вылить воду из второго кувшина, д) отлить из первого кувшина во второй, освободив при этом первый кувшин или долив второй, е) отлить из второго кувшина в первый, освободив при этом второй кувшин или долив первый.

Построение полного дерева поиска решения этой задачи, без каких бы то ни было упрощений, невозможно, поскольку дерево окажется бесконечным: например, можно наполнять первый кувшин, освобождать его, вновь наливать в него воду и т. д. без конца. Конечно, можно ограничить глубину поиска, полагая, что если данная задача имеет какое-то решение, то должен существовать и ведущий к нему путь ограниченной длины. Но даже в этом случае построение соответствующего дерева может привести к слишком громоздкой картине, поскольку каждый последующий ярус дерева будет содержать вершин в шесть раз больше, чем предыдущий. Поэтому разумно ограничить число дуг, исходящих из рассматриваемых вершин, отбрасывая заведомо излишние варианты .

Например, можно отказаться от выполнения в конкретных ситуациях таких элементарных операций, которые не ведут к изменению ситуации (не стоит выливать воду из пустого кувшина или доливать полный!). Тогда первые ярусы дерева поиска будут иметь вид, показанный на рис. 17 (вершины отмечены значениями вектора (р, q), характеризующими соответствующие ситуации, а ребра — символами операций). Однако такое ограничение слабо упрощает дерево поиска.

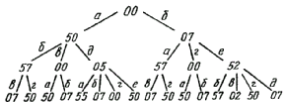
Рис. 17. Первые ярусы дерева поиска с простейшим ограничением.