Положим, что текущая ситуация будет характеризоваться двумя переменными величинами: троичным вектором w, число компонент которого фиксировано и равно числу столбцов в матрице U, и троичной матрицей Т, значениями которой будут служить некоторые миноры матрицы U. Именно перебор значений вектора w должен привести нас к искомому решению, т. е. к вектору v, разумеется, если последний существует.
Положим также, что в текущей ситуации уже определены значения некоторых компонент вектора w, т. е. им приписаны значения 0 или 1, и отыскиваются значения остальных компонент, такие чтобы вектор w стал ортогональным каждой из строк матрицы Т (ее текущего значения), столбцы которой ставятся в соответствие этим компонентам. В начальной ситуации матрица Т совпадает с матрицей U, а вектор w полностью неопределен, т. е. все его компоненты имеют значение « — ».
Элементарный шаг заключается в приписывании значения 0 или 1 некоторой компоненте вектора w или в упрощении матрицы Т путем удаления некоторых строк и столбцов с сохранением нумерации остающихся.
Содержательный анализ данной задачи приводит к нахождению следующих правил редуцирования, применение которых может существенно ускорить поиск решения.
Правило 1. Из матрицы Т удаляются столбцы, не содержащие ни значений 0, ни значений 1.
Правило 2. Из матрицы Т удаляются строки, ортогональные вектору w, а затем столбцы, которым соответствуют компоненты вектора w со значением 0 или 1.
Правило 3. Если в матрице Т имеется строка, где лишь одна компонента обладает значением, отличным от «—», то соответствующей компоненте вектора w приписывается инверсное значение.
Правило 4. Если в матрице Т существует столбец, не содержащий значения 0 (или значения 1), то это значение приписывается соответствующей компоненте вектора w.
Когда редуцирование становится невозможным, производится расщепление текущей ситуации.
Правило расщепления предписывает перебор значений 1 и 0 некоторой компоненты вектора w. При этом рекомендуется выбирать такую компоненту, которая соответствует максимально определенному, т. е. имеющему минимальное число значений «—», столбцу матрицы Г.
Правило нахождения решения. Если непосредственно после удаления некоторой строки из матрицы Т, согласно правилу 2, матрица становится пустой, текущее значение вектора w представляет искомое решение v.
Правило возврата. Если матрица Т становится пустой непосредственно после удаления некоторого столбца или если она содержит строку без значений 0 и 1, то на данной ветви дерева поиска вектор v найти невозможно и следует продолжить обход дерева поиска, возвратившись к последней из точек ветвления с незавершенным перебором.
Правило прекращения поиска. Если при полном обходе дерева поиска вектор v найти не удалось, то это свидетельствует о вырожденности матрицы U.
 |
Договоримся для удобства нумеровать рассматриваемые далее значения переменной матрицы Т, т. е. некоторые миноры (остатки) исходной матрицы U, представляя их как матрицы-константы Т1, Т2, Т3 ц т. д. Положим, что Т1= U.
Непосредственное сокращение матрицы U невозможно, поскольку не выполняются условия применения правил редуцирования. Поэтому воспользуемся правилом расщепления и образуем точку ветвления процесса поиска вектора v, соответствующую выбору значения компоненты а вектора w.
Допустим, что а = 1. Тогда, согласно правилам 2 и 1, определение значений остальных компонент вектора w сводится к поиску вектора, ортогонального матрице
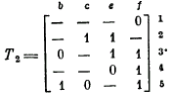 |
Обратив внимание на строку 1 и применяя правило 3, припишем компоненте f вектора w значение 1, после чего
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.