





«Дифференциальные уравнения»
Тесты для самопроверки
Задание 1. Используя определение решения дифференциального уравнения, проверьте,
является ли функция ![]() решением
следующих дифференциальных уравнений:
решением
следующих дифференциальных уравнений:
1.1) ![]() ; 1.2)
; 1.2)
![]() ;
;
1.3) ![]() ; 1.4)
; 1.4)
![]() .
.
Ответы:
|
1.1 |
1.2 |
1.3 |
1.4 |
|
нет |
да |
нет |
да |
Задание 2. Используя представление производной как отношение дифференциалов ![]() , «разделите»
переменные в приведенных ниже дифференциальных уравнениях, т.е. приведите
уравнения к виду
, «разделите»
переменные в приведенных ниже дифференциальных уравнениях, т.е. приведите
уравнения к виду
![]() .
.
2.1) ![]() ; 2.2)
; 2.2)
![]() ; 2.3)
; 2.3) ![]() ;
;
2.4) ![]() ; 2.5)
; 2.5)
![]() .
.
Ответы:
|
2.1 |
2.2 |
2.3 |
2.4 |
2.5 |
|
|
|
|
|
|
Задание 3. Найдите решения дифференциальных уравнений 2.1 - 2.5, которые в результате выполнения задания 2 были приведены к виду, готовому для интегрирования. В задачах 2.1, 2.3 - 2.5 постоянную интегрирования С запишите в логарифмическом виде.
Ответы:
|
2.1 |
|
|
2.2 |
|
|
2.3 |
|
|
2.4 |
|
|
2.5 |
|
Задание 4. Повторите, как распознаются основные типы дифференциальных уравнений первого порядка:
(А) уравнения с разделяющимися переменными;
(Б) однородные уравнения;
(В) линейные уравнения;
(Г) уравнения Бернулли.
Среди приведенных ниже дифференциальных уравнений укажите номера тех уравнений, которые являются уравнениями типа (А) - (Г).
4.1) ![]() ; 4.2)
; 4.2) ![]() ;
4.3)
;
4.3) ![]() ;
;
4.4) ![]() ;
4.5)
;
4.5) ![]() ; 4.6)
; 4.6) ![]() .
.
Ответы:
|
Тип уравнения |
Номера уравнений данного типа |
|
А |
4.2; 4;6 |
|
Б |
4.1; 4.5 |
|
В |
4.3; 4.4 |
|
Г |
4.2; 4.5 |
Задание 5. Вспомните методы интегрирования основных типов (А) - (Г) дифференциальных уравнений первого порядка. Проинтегрируйте уравнения 4.1 - 4.6 из задания 4. Для проверки правильности решения этих уравнений определите, решениями каких из уравнений 4.1 - 4.6 являются приведенные ниже функции (а) - (е):
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) 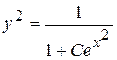 ; е)
; е) ![]() .
.
Ответы:
|
а |
б |
в |
г |
д |
е |
|
4.6 |
4.1 |
4.4 |
4.5 |
4.2 |
4.3 |
Задание 6. Приведенные ниже дифференциальные уравнения 2-го порядка разбейте на
три группы. К группе А отнесите те дифференциальные уравнения, которые содержат
только вторую производную ![]() и
независимую переменную х; к группе Б - те уравнения, которые не содержат
неизвестной функции у; к группе В - уравнения, не содержащие независимой
переменной х.
и
независимую переменную х; к группе Б - те уравнения, которые не содержат
неизвестной функции у; к группе В - уравнения, не содержащие независимой
переменной х.
6.1) ![]() ; 6.2)
; 6.2)
![]() ; 6.3)
; 6.3) 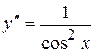 ;
;
6.4) ![]() ; 6.5)
; 6.5)
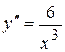 ; 6.6)
; 6.6) ![]() .
.
Ответы:
|
А |
Б |
В |
|
6.3; 6.5 |
6.2; 6.6 |
6.1; 6.4 |
Задание 7. Вспомните методы понижения порядка для неполных дифференциальных уравнений 2-го порядка. Опираясь на схемы-подсказки, проинтегрируйте уравнения группы А (подсказка 1), группы Б (подсказка 2) и группы В (подсказка 3).
Подсказка 1
|
Если уравнение имеет вид
|
Подсказка 2
|
Если уравнение не содержит неизвестной функции у,
то нужно ввести новую неизвестную функцию |
Подсказка 3
|
Если уравнение не содержит независимой переменной х,
то нужно объявить у - новой независимой переменной, а |
Для проверки правильности полученных результатов определите, решениями каких дифференциальных уравнений 6.1 - 6.6 являются приведенные ниже функции.
7.1) ![]() ; 7.2)
; 7.2)
![]() ;
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.