«Ряды»
Тесты для самопроверки
1. Необходимый признак сходимости ряда.
|
Теорема (необходимый признак сходимости). Если ряд Следствие (достаточное условие расходимости ряда). Если Важно! Если |
Задание 1. Среди следующих рядов
1) 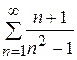 ; 2)
; 2) 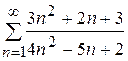 ; 3)
; 3) 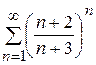 ;
;
4) 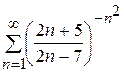 ; 5)
; 5) 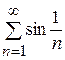 ; 6)
; 6) 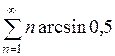 , найдите те, для
которых справедливы утверждения:
, найдите те, для
которых справедливы утверждения:
а) ![]() ; б)
; б) ![]() ;
;
в) ряд сходится; г) ряд расходится.
Правильные ответы:
|
№ ряда |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
0 |
|
|
0 |
0 |
|
|
сходится или расходится |
неизвестно |
расходится |
расходится |
неизвестно |
неизвестно |
расходится |
2. Признаки сравнения.
|
Теорема (признак сравнения). Пусть 1) ряд Важно! При решении использовать: а) ряд Дирихле б) геометрическую прогрессию |
Задание 2. Найти верные оценки для ![]() :
:
2.1) 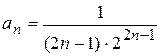 ; 2.2)
; 2.2) 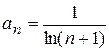 ;
;
2.3) 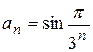 ; 2.4)
; 2.4)
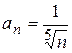 ; 2.5)
; 2.5) 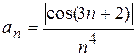 .
.
Варианты ответов
|
1 |
2 |
3 |
|
|
2.1 |
|
|
|
|
2.2 |
|
|
|
|
2.3 |
|
|
|
|
2.4 |
|
|
|
|
2.5 |
|
|
|
Правильные ответы (номера):
|
2.1 |
2.2 |
2.3 |
2.4 |
2.5 |
|
1 |
2 |
2 |
3 |
1 |
Задание 3. Используя признак сравнения, среди рядов, приведенных в задании 2, найти сходящиеся и расходящиеся.
Правильные ответы:
|
сходится |
1, 3, 5 |
|
расходится |
2, 4 |
|
Теорема (предельный признак сравнения). Пусть |
Задание 4. Используя предельный признак сравнения, исследовать на сходимость ряды
с общими членами ![]() :
:
4.1) 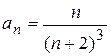 ; 4.2)
; 4.2)
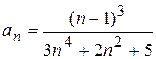 ;
;
4.3) 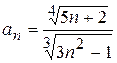 ; 4.4)
; 4.4)
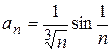 .
.
Указание: Использовать для сравнения подходящий ряд Дирихле.
Правильные ответы:
|
№ |
С каким рядом |
|
Сходится или расходится |
|
4.1 |
|
|
сходится |
|
4.2 |
|
|
расходится |
|
4.3 |
|
|
расходится |
|
4.4 |
|
|
сходится |
|
Теорема (признак сравнения в эквивалентной форме). Пусть Важно! При решении нужно использовать таблицу эквивалентных функций:
А также тот факт,
что |
Задание 5. Используя признак сравнения в эквивалентной форме, найти для 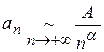 и сделать вывод о
сходимости следующих рядов:
и сделать вывод о
сходимости следующих рядов:
5.1) 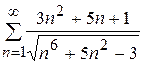 ; 5.2)
; 5.2) 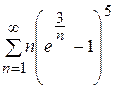 ; 5.3)
; 5.3) 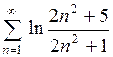 ; 5.4)
; 5.4) 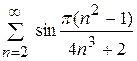 ; 5.5)
; 5.5) 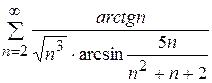 .
.
Варианты ответов:
1) 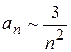 , сходится; 2)
, сходится; 2)
![]() , сходится;
, сходится;
3) ![]() , сходится; 4)
, сходится; 4)
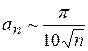 , расходится;
, расходится;
5) 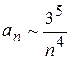 , сходится; 6)
, сходится; 6)
![]() , расходится;
, расходится;
7) ![]() , расходится; 8)
, расходится; 8)
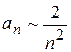 , сходится.
, сходится.
Правильные ответы (номера):
|
5.1 |
5.2 |
5.3 |
5.4 |
5.5 |
|
6 |
5 |
8 |
7 |
4 |
3. Признак Даламбера.
|
Теорема (признак Даламбера). Пусть Важно! Если |
Задание 6. Найти ![]() , если
, если
6.1) 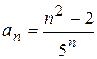 ; 6.2)
; 6.2)
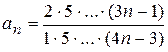 ;
;
6.3) 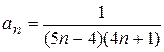 ; 6.4)
; 6.4) 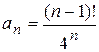 ;
;
6.5) 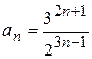 ; 6.6)
; 6.6)
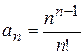 .
.
Варианты ответов
|
6.1 |
|
|
|
|
6.2 |
|
|
|
|
6.3 |
|
|
|
|
6.4 |
|
|
|
|
6.5 |
|
|
|
|
6.6 |
|
|
|
Правильные ответы (номера):
|
6.1 |
6.2 |
6.3 |
6.4 |
6.5 |
6.6 |
|
2 |
1 |
3 |
1 |
2 |
3 |
Задание 7. Исследовать сходимость рядов из задания 6, вычисляя 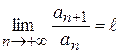 и применяя признак
Даламбера.
и применяя признак
Даламбера.
Варианты ответов:
7.1) ![]() , сходится; 7.2)
, сходится; 7.2)
![]() , расходится;
, расходится;
7.3) ![]() , сходится; 7.4)
, сходится; 7.4)
![]() , расходится;
, расходится;
7.5) ![]() , сходится; 7.6)
, сходится; 7.6)
![]() , вывод сделать нельзя;
, вывод сделать нельзя;
7.7) ![]() , расходится; 7.8)
, расходится; 7.8)
![]() , сходится.
, сходится.
Правильные ответы (номера):
|
7.1 |
7.2 |
7.3 |
7.4 |
7.5 |
7.6 |
|
3 |
5 |
6 |
2 |
1 |
7 |
4. Радикальный признак Коши.
|
Теорема (признак Коши). Пусть Важно! Если Важно! |
Задание 8. Вычислить ![]() и, используя
признак Коши, исследовать сходимость следующих рядов:
и, используя
признак Коши, исследовать сходимость следующих рядов:
8.1) 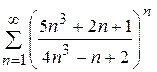 ; 8.2)
; 8.2)
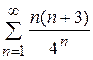 ;
;
8.3) 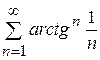 ; 8.4)
; 8.4) 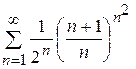 ; 8.5)
; 8.5) 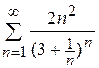 .
.
Варианты ответов:
8.1) ![]() , сходится; 8.2)
, сходится; 8.2)
![]() , расходится;
, расходится;
8.3) ![]() , сходится; 8.4)
, сходится; 8.4) ![]() , сходится; 8.5)
, сходится; 8.5) ![]() , сходится;
, сходится;
8.6) ![]() , расходится; 8.7)
, расходится; 8.7) ![]() , сходится.
, сходится.
Правильные ответы (номера):
|
8.1 |
8.2 |
8.3 |
8.4 |
8.5 |
|
6 |
4 |
3 |
2 |
1 |
5. Интегральный признак Коши.
|
Теорема (интегральный признак Коши). Если члены знакоположительного ряда 1) если 2) если |
Задание 9. Применить интегральный признак для исследования сходимости рядов:
9.1) 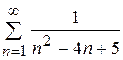 ; 9.2)
; 9.2)
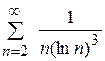 ;
;
9.3) 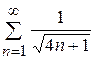 ; 9.4)
; 9.4)
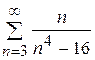 .
.
Указать вид первообразной ![]() для
для ![]() и
и 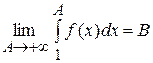 .
.
Варианты ответов
1) ![]() , расходится;
, расходится;
2) ![]() , сходится;
, сходится;
3) 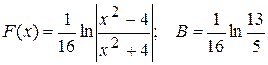 , сходится;
, сходится;
4) 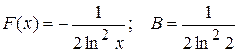 , сходится.
, сходится.
Правильные ответы (номера):
|
9.1 |
9.2 |
9.3 |
9.4 |
|
2 |
4 |
1 |
3 |
6. Знакочередующие ряды. Признак Лейбница. Знакопеременные ряды.
|
Теорема (признак Лейбница). Знакочередующийся ряд 1) последовательность абсолютных величин членов ряда
монотонно убывает, т.е. 2) общий член ряда стремится к нулю: При этом сумма S ряда удовлетворяет неравенству: Важно! Если Если члены ряда Определение. Знакопеременный ряд Важно! Для исследования абсолютной сходимости к рядам Важно! Признак Лейбница - это признак условной сходимости рядов. |
Задание 10. Даны ряды:
10.1) 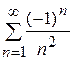 ; 10.2)
; 10.2)
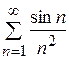 ; 10.3)
; 10.3) 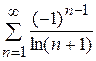 ;
;
10.4) 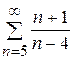 ; 10.5)
; 10.5)
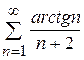 ; 10.6)
; 10.6) 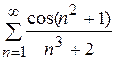 ;
;
10.7) 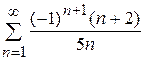 ; 10.8)
; 10.8) 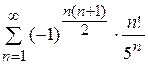 .
.
Выберите из них те, которые удовлетворяют условиям:
а) знакочередующиеся;
б) знакопеременные;
в) знакоположительные.
Правильные ответы (номера):
|
а |
б |
в |
|
1, 3, 7 |
2, 6, 8 |
4, 5 |
Задание 11. Для знакочередующихся рядов из задания 10 проверить выполнены ли условия признака Лейбница.
Правильные ответы:
1) да; 3) да; 7) нет.
Задание 12. Из знакочередующихся и знакопеременных рядов задания 10 найти:
а) абсолютно сходящиеся;
б) условно сходящиеся;
в) расходящиеся.
Правильные ответы:
а) абсолютно сходятся: 10.1; 10.2; 10.6;
б) условно сходятся: 10.3;
в) расходятся: 10.7; 10.8.
Задание 13. Вычислить сумму S ряда 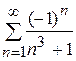 с
точностью:
с
точностью:
1) 0,15; 2) 0,02; 3) 0,01.
Сколько n членов ряда при этом надо взять?
Варианты ответов:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
Правильные ответы (номера):
|
13.1 |
13.2 |
13.3 |
|
3 |
1 |
2 |
7. Степенные ряды.
|
Степенным рядом называется ряд вида
или вида
где |
|
Теорема Абеля. Если степенной ряд (1) сходится при Из теоремы Абеля вытекает, что степенной ряд (1)
сходится в интервале (-R, R) и расходится вне этого интервала. Число R
называется радиусом сходимости. При R = 0 ряд (1) сходится в единственной точке
х = 0, при Для ряда (2) интервал сходимости имеет вид: Формулы для нахождения радиуса сходимости имеют вид:
|
Задание 14. Даны степенные ряды:
14.1) 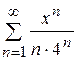 ; 14.2)
; 14.2)
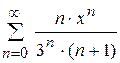 ; 14.3)
; 14.3) 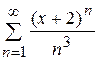 ;
;
14.4) 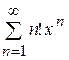 ; 14.5)
; 14.5) 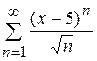 ; 14.6)
; 14.6) 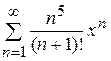 .
.
Найти: а) радиус сходимости; б) интервал сходимости; в) область сходимости.
Варианты ответов:
а) радиус сходимости:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() .
.
б) интервал сходимости:
1) ![]() ; 2)
; 2) ![]() ; 3) точка
; 3) точка ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) ![]() .
.
в) область сходимости:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ;
;
6) ![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() ; 9) точка
; 9) точка ![]() .
.
Правильные ответы (номера):
|
14.1 |
14.2 |
14.3 |
14.4 |
14.5 |
14.6 |
|
|
а |
4 |
2 |
6 |
1 |
6 |
3 |
|
б |
7 |
1 |
5 |
3 |
6 |
4 |
|
в |
1 |
5 |
8 |
9 |
3 |
7 |
8. Применение степенных рядов.
Запишите разложения в ряд Тейлора некоторых элементарных функций: ![]() .
.
Задание 15. Зная разложение в степенной ряд элементарных функций, разложить в ряд Маклорена следующие функции:
15.1) ![]() ; 15.2)
; 15.2)
![]() ;
;
15.3) ![]() ; 15.4)
; 15.4)
![]() .
.
Варианты ответов:
1) 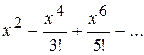 ; 2)
; 2) 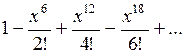 ;
;
3) 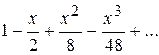 ; 4)
; 4) 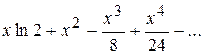 .
.
Правильные ответы (номера):
|
15.1 |
15.2 |
15.3 |
15.4 |
|
3 |
1 |
2 |
4 |
Задание 16. Найти разложение в ряд первообразных ![]() функций
функций
![]() из задания 15,
проинтегрировав соответствующие степенные ряды их в пределах от 0 до х.
из задания 15,
проинтегрировав соответствующие степенные ряды их в пределах от 0 до х.
Варианты ответов:
16.1) 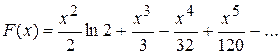 ;
;
16.2) 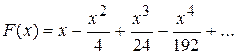 ;
;
16.3) 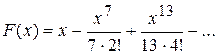 ;
;
16.4) 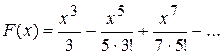 .
.
Правильные ответы (номера):
|
16.1 |
16.2 |
16.3 |
16.4 |
|
2 |
4 |
3 |
1 |
Для того, чтобы найти сумму ряда с заданной степенью точности
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.