7.3) ![]() ; 7.4)
; 7.4)
![]() ;
;
7.5) ![]() ; 7.6)
; 7.6)
![]() .
.
Ответы:
|
7.1 |
7.2 |
7.3 |
7.4 |
7.5 |
7.6 |
|
6.5 |
6.3 |
6.1 |
6.6 |
6.4 |
6.2 |
Задание 8. Для каждого из линейных однородных дифференциальных уравнений 8.1 - 8.7 с постоянными коэффициентами составьте характеристическое уравнение, найдите его корни и напишите (в зависимости от характера корней) общее решение уравнения
Подсказка 1
|
Если линейное однородное уравнение имеет вид |
Подсказка 2
|
Если корни |
1)действительные различные
|
2) действительные
равные |
3) комплексно-сопряженные
|
|
|
|
|
8.1) ![]() ; 8.2)
; 8.2)
![]() ;
;
8.3) ![]() ; 8.4)
; 8.4)
![]() ; 8.5)
; 8.5)
![]() ;
;
8.6) ![]() ; 8.7)
; 8.7)
![]() .
.
Для проверки правильности выполнения задания каждой функции 8.А - 8.Ж из списка приведенных ответов поставьте в соответствие номер той из задач 8.1 - 8.7, общим решением которой она является.
8.А. ![]() ; 8.Б.
; 8.Б.
![]() ;
;
8.В. ![]() ; 8.Г.
; 8.Г.
![]() ;
;
8.Д. ![]() ; 8.Е.
; 8.Е.
![]() ;
;
8.Ж. ![]() .
.
Ответы:
|
8.А |
8.Б |
8.В |
8.Г |
8.Д |
8.Е |
8.Ж |
|
8.6 |
8.4 |
8.3 |
8.7 |
8.1 |
8.5 |
8.2 |
Задание 9. Даны линейные неоднородные дифференциальные уравнения 2-го порядка со специальной правой частью. Повторите метод подбора частного решения ỹ для таких уравнений. Напишите частные решения уравнений 9.1 - 9.4, не находя числовых значений их коэффициентов.
Подсказка
|
Дано уравнение 1. Если
3.
|
9.1) ![]() ; 9.2)
; 9.2)
![]() .
.
9.3) ![]() ; 9.4)
; 9.4)
![]() .
.
Из списка приведенных ответов 9.А - 9.Р выберите верные, присвоив им номера тех из уравнений 9.1 - 9.4, решениями которых они являются.
9.А. ![]() ; 9.Б.
; 9.Б.
![]() ;
;
9.В. ![]() ; 9.Г.
; 9.Г.
![]() ;
;
9.Д. ![]() ; 9.Е.
; 9.Е.
![]() ;
;
9.Ж. ![]() ; 9.И.
; 9.И.
![]() ;
;
9.К. ![]() ;
9.Л.
;
9.Л. ![]() ;
;
9.М. ![]() ; 9.Н.
; 9.Н.
![]() ;
;
9.О. ![]() ;
;
9.Р. ![]() .
.
Ответы:
|
9.1 |
9.2 |
9.3 |
9.4 |
|
9.В |
9.Е |
9.Л |
9.Р |
Задание 10. Даны 2 матрицы
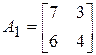 ;
; 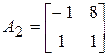 .
.
а) Найдите собственные значения ![]() и
и ![]() матриц
матриц ![]() и
и ![]() и укажите их
среди данных пар чисел 10.1 - 10.5:
и укажите их
среди данных пар чисел 10.1 - 10.5:
10.1 {1; 1}; 10.2. {1; 10}; 10.3. {1; 3};
10.4. {-3; 3}; 10.5. {-3; -3}.
Ответы:
|
|
|
|
10.2 |
10.4 |
б) Найдите собственные векторы матриц ![]() и
и ![]() и укажите их
среди следующих пар векторов 10.6 - 10.9.
и укажите их
среди следующих пар векторов 10.6 - 10.9.
10.6. 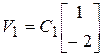 ,
, 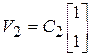 ;
;
10.7. 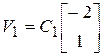 ,
, 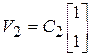 ;
;
10.8. 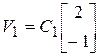 ,
, 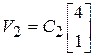 ;
;
10.9. 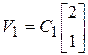 ,
, 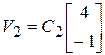 .
.
Ответы:
|
|
|
|
10.6 |
10.9 |
Задание 11. Решите системы линейных однородных дифференциальных уравнений 11.1, 11.2 с постоянными коэффициентами, используя алгоритм, приведенный в схеме-подсказке.
Подсказка
|
Пусть дана система 1. Напишем матрицу системы 2. Найдем ее собственные значения 3. Определим собственные векторы 4. Составим общее решение системы в векторном виде:
|
11.1. 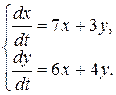 11.2.
11.2.
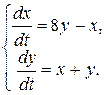
Среди приведенных ответов 11.А - 11.Г выберите верные.
11.А. 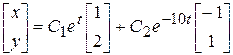 .
.
11.Б. 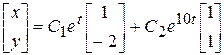 .
.
11.В. 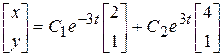 .
.
11.Г. 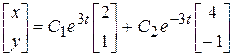 .
.
Ответы:
|
11.1 |
11.2 |
|
11.Б |
11.Г |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.