Синтез цифровых схем арифметических устройств (исходные операнды - десятичные числа: Мн = 28,69, Мт = 21,59; алгоритм выполнения операции умножения ¾ “Б”)

оценки погрешности сложения полученная сумма  приводится к нулевому порядку, а затем переводится в десятичную систему счисления:

Сумма ₄ =  302,101      Рсум ₄ = 0.00

Сумма ₁₀ = 50,27

Результат прямого сложения операндов дает следующее значение:

А+Б₁₀ = 28,69 + 21,59 = 50,28

Абсолютная погрешность:

∆= 50,28 – 50,27=0,01

Относительная погрешность:

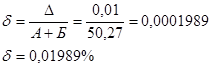
Эта погрешность является суммарной, накопленной за счет приближенного перевода из 10 с/с в четверичную обоих слагаемых.

5. Разработка структурной схемы сумматора-умножителя

Структурная схема сумматора-умножителя 2-го типа для алгоритма умножения «Б»:

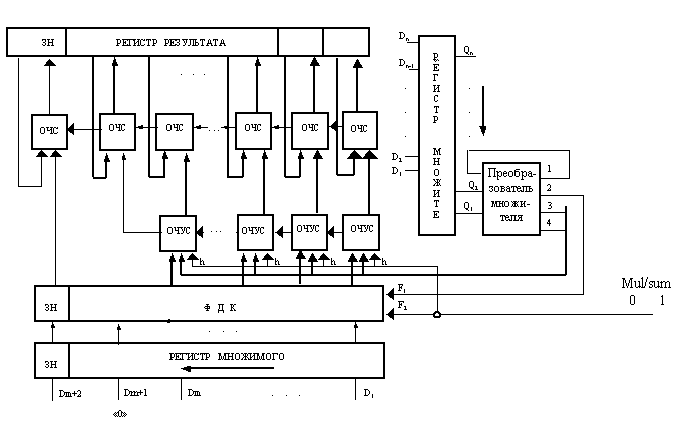
Данная схема может работать в двух режимах:

1.  Как сумматор (на входе mul/sum – “1”). Оба слагаемых последовательно заносятся в регистр множимого, после чего они проходят через ОЧУС не изменяясь и складываются в ОЧС.

2.  Как умножитель (на входе mul/sum – “0”).

В ФДК формируется дополнительный код множимого (если пара множителя отрицательная).

Принцип действия  - в следующей таблице

Таблица 2

F1          F2	РЕЗУЛЬТАТ НА ВЫХОДАХ ФДК
0           0	Доп. код множимого
0           1	Доп. код слагаемого
1           0	Меняет знак Мн
1           1	Меняет знак слагаемого

В преобразователь множителя (ПМ) из регистра множителя поступает двоичо – четверичная пара, которая, если необходимо, преобразуется определённым образом. После чего она поступает на входы ОЧУС.

В ОЧУС  множимое умножается на пару множителя с учётом переносов.

В ОЧС складываются результат из ОЧУС и частичная сумма предыдущего результата.   

В Регистре результата храняться частичные суммы.

Временные затраты на умножение шестиразрядных сомножителей определяются :

T_у = 6(11t_ОЧУС+11t_ОЧС+t_сдв)

где:     t_сдв      ¾ время сдвига множимого;

t_ОЧУС  ¾ время формирования единицы переноса из одного ОЧУС в другой (умножение происходит последовательно во всех ОЧУС);

t_ОЧС    ¾ время формирования единицы переноса в ОЧС (для последнего ОЧС это время сложения слагаемых);

6. Разработка функциональных схем основных узлов сумматора-умножителя

6.1 Логический синтез одноразрядного четверичного умножителя

ОЧУС - это комбинационное устройство, имеющее 6 входов (2 разряда из регистра Мн, 2 разряда из регистра Мт,управляющий вход h и перенос p) и 3 выхода. Принцип работы ОЧУС описывается с помощью таблицы истинности .

Разряды множителя закодированы : 0 - 00; 1 - 01; 2 - 10; 3 - 11.

Разряды множимого закодированы : 0 - 01; 1 - 10; 2 - 11; 3 – 00.

Управляющий вход h определяет тип операции: 0 - умножение закодированных цифр, поступивших на информационные входы; 1 - вывод на выходы без изменения значения разрядов, поступивших из регистра множимого.

На вход ОЧУC из разрядов множителя не может поступить код 11, при работу ОЧУС как сумматора на вход переноса не может поступить 1, а при умножении на 0 или 1 на вход переноса не может поступить 1. 

Таблица 3

Пер.	Мн		Мт		Упр.		Перенос	Результат		Результат операции
Р1	Х1	Х2	У1	У2	H		Р	Q1	Q2	в четверичной с/с
0	0	0	0	0	0		0	0	1	3*0+0=00
0	0	0	0	0	1		0	0	0	выход - код «03»
0	0	0	0	1	0		0	0	0	3*1+0=03
0	0	0	0	1	1		0	0	0	Выход - код «03»
0	0	0	1	0	0		1	1	1	3*2+0=12
0	0	0	1	0	1		0	0	0	выход - код «03»
0	0	0	1	1	0		X	X	X	3*3+0=21	*
0	0	0	1	1	1		X	X	X	выход - код «03»	*
0	0	1	0	0	0		0	0	1	0*0+0=00
0	0	1	0	0	1		0	0	1	выход - код «00»
0	0	1	0	1	0		0	0	1	0*1+0=00
0	0	1	0	1	1		0	0	1	выход - код «00»
0	0	1	1	0	0		0	0	1	0*2+0=00
0	0	1	1	0	1		0	0	1	выход - код «00»
0	0	1	1	1	0		Х	Х	Х	0*3+0=00	*
0	0	1	1	1	1		Х	Х	Х	выход - код «00»	*
0	1	0	0	0	0		0	0	1	1*0+0=00
0	1	0	0	0	1		0	1	0	Выход - код «01»
0	1	0	0	1	0		0	1	0	1*1+0=01
0	1	0	0	1	1		0	1	0	выход - код «01»
0	1	0	1	0	0		0	1	1	1*2+0=02
0	1	0	1	0	1		0	1	0	Выход - код «01»
0	1	0	1	1	0		Х	Х	Х	1*3+0=03	*
0	1	0	1	1	1		Х	Х	Х	выход - код «01»	*
0	1	1	0	0	0		0	0	1	2*0+0=00
0	1	1	0	0	1		0	1	1	Выход - код «02»
0	1	1	0	1	0		0	1	1	2*1+0=02
0	1	1	0	1	1		0	1	1	выход - код «02»
0	1	1	1	0	0		1	0	1	2*2+0=10
0	1	1	1	0	1		0	1	1	выход - код «02»
0	1	1	1	1	0		Х	Х	Х	2*3+0=12	*
0	1	1	1	1	1		Х	Х	Х	выход - код «02»	*
1	0	0	0	0	0		X	X	X	3*0+1=01	*
1	0	0	0	0	1		X	X	X	выход - код «03»	*
1	0	0	0	1	0		X	X	X	3*1+1=10	*
1	0	0	0	1	1		X	X	X	выход – код «03»	*
1	0	0	1	0	0		1	0	0	3*2+1=13
1	0	0	1	0	1		X	X	X	Выход - код «03»	*
1	0	0	1	1	0		X	X	X	3*3+1=22	*
1	0	0	1	1	1		X	X	X	Выход - код «03»	*
1	0	1	0	0	0		X	X	X	0*0+1=01	*
1	0	1	0	0	1		X	X	X	выход - код «00»	*
1	0	1	0	1	0		X	X	X	0*1+1=01	*
1	0	1	0	1	1		X	X	X	выход - код «00»	*
1	0	1	1	0	0		0	1	0	0*2+1=01
1	0	1	1	0	1		X	X	X	выход – код «00»	*
1	0	1	1	1	0		X	X	X	0*3+1=01	*
1	0	1	1	1	1		X	X	X	выход – код «00»	*
1	1	0	0	0	0		X	X	X	1*0+1=01	*
1	1	0	0	0	1		X	X	X	выход - код «01»	*
1	1	0	0	1	0		X	X	X	1*1+1=02	*
1	1	0	0	1	1		X	X	X	выход - код «01»	*
1	1	0	1	0	0		0	0	0	1*2+1=03
1	1	0	1	0	1		X	X	X	выход – код «01»	*
1	1	0	1	1	0		X	X	X	1*3+1=10	*
1	1	0	1	1	1		X	X	X	выход - код «01»	*
1	1	1	0	0	0		X	X	X	2*0+1=01	*
1	1	1	0	0	1		X	X	X	выход - код «02»	*
1	1	1	0	1	0		X	X	X	2*1+1=03	*
1	1	1	0	1	1		X	X	X	выход - код «02»	*
1	1	1	1	0	0		1	1	0	2*2+1=11
1	1	1	1	0	1		X	X	X	выход - код «02»	*
1	1	1	1	1	0		X	X	X	2*3+1=13	*
1	1	1	1	1	1		X	X	X	выход - код «02»	*

Минимизация функций выходов

Минимизацию выхода Q2 проведем с использованием карты Карно-Вейча, а P и Q1 - с использованием алгоритма Рота:

Выход P

1)Поиск простых импликант

В результате выполнения пяти операций звездчатого умножения (см. табл.1 приложения) были найдены следующие простые импликанты:

Z={111x00, 11110x, x001x0, x111x0, 100xxx, xxx11x, 1xx0xx, 1xxxx1, 1xxx1x,}

2)Поиск L-экстремалей

Для поиска L-экстремалей применим операцию решетчатого вычитания (см. табл.2 приложения). Результат операции указывает, какие импликанты из множества Z стали L-экстремалями:

E={x001x0, x111x0, xxx11x, 1xx0xx, 1xxxx1}

3)Проверка L-экстремалей

В результате проверки (см. табл.3 приложения) было выяснено, что только кубы x001x0 и x111x0 стали L-экстремалями за счет множества L.

4)Поиск  непокрытых исходных наборов

Поиск (см. табл.4 приложения) показал отсутствие непокрытых наборов (L-экстремали покрывают все кубы из множества L)

 

F_min={x001x0, x111x0}=

5)Проверка

X1

1

1

Y1

*

*

1

*

*

1

P1

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

Y2

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

P1

X2

H

H

Выход Q1

1)Поиск простых импликант

В результате выполнения пяти операций звездчатого умножения (см. табл.5 приложения) были найдены следующие простые импликанты:

Z={0x01x0, 0101xx, 1x1x00, 1x110x, x1xxx1, x1xx1x, xxx11x, 1xx0xx, 1xxxx1, 1xxx1x}

2)Поиск L-экстремалей

Для поиска L-экстремалей применим операцию решетчатого вычитания (см. табл.6 приложения). Результат операции указывает, какие импликанты из множества Z стали L-экстремалями:

E={1xxxx1, 1xx0xx, xxx11x, x1xx1x, x1xxx1, 0x01x0}

3)Проверка L-экстремалей

В результате проверки (см. табл.7 приложения) было выяснено, что только кубы x1xx1x, x1xxx1 и 0x01x0 стали L-экстремалями за счет множества L.

4)Поиск  непокрытых исходных наборов

Поиск (см. табл.8 приложения) показал наличие непокрытых наборов.

5)Поиск покрытия оставшихся кубов

Для покрытия кубов 101100 и 111100 воспользуемся операцией