основании
сравнения строим куб 
, в котором поглощенная координата заменяется символом x.
={101x1, 1x101}.
Сравним попарно 
и 
:
|
|
||
|
|
11111 |
|
|
10111 |
1x111 |
|
|
11101 |
111x1 |
На основании
сравнения строим куб 
, в котором поглощенная координата заменяется символом x.
={1x111, 111x1}.
Разобьем все 1-кубы на четыре группы в зависимости от положения независимой координаты x:
|
|
|
|
|
|
000x1 |
0x001 |
100x0 |
1x000 |
|
001x0 |
0x011 |
101x1 |
1x010 |
|
010x1 |
0x100 |
110x0 |
1x101 |
|
011x0 |
0x110 |
111x1 |
1x111 |
Cклеим 
и 
, 
и 
, 
внутри каждой группы:
|
0x0x1 |
0x0x1 |
1x0x0 |
1x0x0 |
|
0x1x0 |
0x1x0 |
1x1x1 |
1x1x1 |
На основании
склеивания, формируем получившиеся 2-кубы:
={0x0x1, 0x1x0}, 
={0x0x1, 0x1x0}, 
={1x0x0, 1x1x1}, 
={1x0x0, 1x1x1}.
Сформируем все 2-кубы в одну группу склеивания в зависимости от положения независимой координаты x:
|
|
|
0x0x1 |
|
0x1x0 |
|
1x0x0 |
|
1x1x1 |
Очевидно, единственный
2-куб 
={ 0x0x1, 0x1x0, 1x0x0, 1x1x1} больше не склеивается и представляет
собой конечный результат склеивания. Построим таблицу покрытия всех склеенных
получившихся кубов и первичных импликант:
|
00001 |
00011 |
00100 |
00110 |
01001 |
01011 |
01100 |
01110 |
10000 |
10010 |
10101 |
10111 |
11000 |
11010 |
11101 |
11111 |
|
|
0x0x1 |
v |
v |
v |
v |
||||||||||||
|
0x1x0 |
v |
v |
v |
v |
||||||||||||
|
1x0x0 |
v |
v |
v |
v |
||||||||||||
|
1x1x1 |
v |
v |
v |
v |
Найдем кубы, которые осуществляют минимальное покрытие термов 00001, 00011, 00100, 00110, 01001, 01011, 01100, 01110, 10000, 10010, 10101, 10111, 11000, 11010, 11101, 11111. Ими будут являться кубы 0x0x1, 0x1x0, 1x0x0, 1x1x1.
После минимизация функция S1 будет иметь следующий вид:
S1=
Функция для реализации в заданном базисе будет иметь вид:
S1 = (
Минимизация S2
Произведём минимизацию функции S2 при помощи метода Квайна – Мак-Класки. Для этого выпишем из таблицы истинности все 0-кубы:
={00000, 00001, 00100, 00111, 01010, 01011, 01101,
01110, 10000, 10011, 10110, 10111, 11001, 11010, 11100, 11101}.
Разобьем 0-кубы на 5 групп по количеству единиц в каждом двоичном наборе:
={00000};
={00001, 00100, 10000};
={01010};
={00111, 01011, 01101, 01110, 10011, 10110, 11001, 11010, 11100};
={10111, 11101};
Сравним попарно и :
|
|
||||
|
|
00001 |
00100 |
10000 |
|
|
00000 |
0000x |
00x00 |
x0000 |
На основании
сравнения строим куб 
, в котором поглощенная координата заменяется символом x.
={0000x, 00x00, x0000}.
Сравним попарно и :
|
|
||
|
|
01010 |
|
|
00001 |
||
|
00100 |
||
|
10000 |
На основании
сравнения куб получился пустым.
Сравним попарно и :
|
|
||||||||||
|
|
00111 |
01011 |
01101 |
01110 |
10011 |
10110 |
11001 |
11010 |
11100 |
|
|
01010 |
0101x |
01x10 |
x1010 |
На основании
сравнения строим куб , в котором поглощенная координата заменяется символом x.
={0101x, 01x10, x1010}.
Сравним попарно и :
|
|
|||
|
|
10111 |
11101 |
|
|
00111 |
x0111 |
||
|
01011 |
|||
|
01101 |
x1101 |
||
|
01110 |
|||
|
10011 |
10x11 |
||
|
10110 |
1011x |
||
|
11001 |
11x01 |
||
|
11010 |
|||
|
11100 |
1110x |
На основании
сравнения строим куб , в котором поглощенная координата заменяется символом x.
={ x0111, 10x11, 1011x, x1101, 11x01, 1110x}.
Разобьем все 1-кубы на три группы в зависимости от положения независимой координаты x:
|
|
|
|
|
0000x |
00x00 |
x0000 |
|
0101x |
01x10 |
x0111 |
|
1011x |
10x11 |
x1010 |
|
1110x |
11x01 |
x1101 |
Очевидно, что при
склеивании не получается кубов новой размерности, следовательно кубы , 
являются конечными.
Построим таблицу покрытия всех склеенных получившихся кубов и первичных импликант:
|
00000 |
00001 |
00100 |
00111 |
01010 |
01011 |
01101 |
01110 |
10000 |
10011 |
10110 |
10111 |
11001 |
11010 |
11100 |
11101 |
|
|
0000x |
v |
v |
||||||||||||||
|
0101x |
v |
v |
||||||||||||||
|
1011x |
v |
v |
||||||||||||||
|
1110x |
v |
v |
||||||||||||||
|
00x00 |
v |
v |
||||||||||||||
|
01x10 |
v |
v |
||||||||||||||
|
10x11 |
v |
v |
||||||||||||||
|
11x01 |
v |
v |
||||||||||||||
|
x0000 |
v |
v |
||||||||||||||
|
x0111 |
v |
v |
||||||||||||||
|
x1010 |
v |
v |
||||||||||||||
|
x1101 |
v |
v |
Найдем кубы, которые осуществляют минимальное покрытие термов 00000, 00001, 00100, 00111, 01010, 01011, 01101, 01110, 10000, 10011, 10110, 10111, 11001, 11010, 11100, 11101. Ими будут являться кубы 0000x, 0101x, 1011x, 1110x, 00x00, 01x10, 10x11, 11x01, x0000, x0111, x1010, x1101
После минимизация функция S2 будет иметь следующий вид:
S2 =
Функция для реализации в заданном базисе будет иметь вид: 
S2 =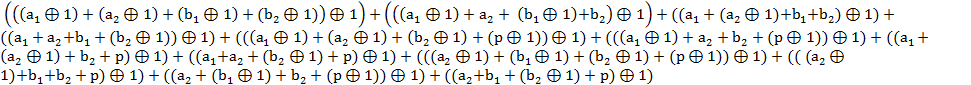
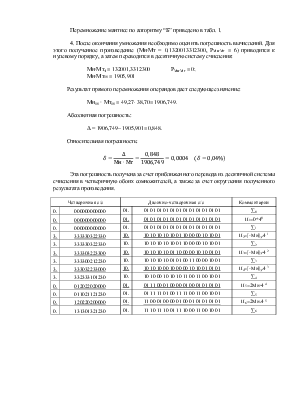
Мультиплексор – это логическая схема, имеющая n информационных входов, m управляющих входов и один выход. При этом должно выполняться условие n = 2m.На выход мультиплексора может быть пропущен без изменений любой (один) логический сигнал, поступающий на информационные входы. Порядковый номер информационного входа, значение с которого в данный момент должно быть передано на выход, определяется двоичным кодом на управляющих входах.
Для синтеза ОЧС будем использовать мультиплексор “один из восьми” (1 из 8ми).
Входы I0,I1,…, I3 - это информационные входы мультиплексора. Сигналы х1 могут принимать значения 0 или 1. Входы S0 ,S1 , S2 - управляющие входы.
Таблица истинности для ОЧС на мультиплексорах
|
a1a2b1 |
b2p |
П |
Псхема |
S1 |
S1схема |
S2 |
S2схема |
|
000 |
00 |
1 |
|
0 |
p |
1 |
|
|
01 |
1 |
1 |
1 |
||||
|
10 |
0 |
0 |
0 |
||||
|
11 |
0 |
1 |
0 |
||||
|
001 |
00 |
1 |
|
1 |
|
1 |
|
|
01 |
1 |
0 |
0 |
||||
|
10 |
0 |
1 |
0 |
||||
|
11 |
1 |
0 |
1 |
||||
|
010 |
00 |
0 |
|
0 |
p |
0 |
|
|
01 |
0 |
1 |
0 |
||||
|
10 |
0 |
0 |
1 |
||||
|
11 |
0 |
1 |
1 |
||||
|
011 |
00 |
0 |
|
1 |
|
0 |
|
|
01 |
1 |
0 |
1 |
||||
|
10 |
0 |
1 |
1 |
||||
|
11 |
0 |
0 |
0 |
||||
|
100 |
00 |
1 |
|
1 |
|
1 |
|
|
01 |
1 |
0 |
0 |
||||
|
10 |
0 |
1 |
0 |
||||
|
11 |
1 |
0 |
1 |
||||
|
101 |
00 |
1 |
const 1 |
0 |
p |
0 |
|
|
01 |
1 |
1 |
0 |
||||
|
10 |
1 |
0 |
1 |
||||
|
11 |
1 |
1 |
1 |
||||
|
110 |
00 |
0 |
|
1 |
|
0 |
|
|
01 |
1 |
0 |
1 |
||||
|
10 |
0 |
1 |
1 |
||||
|
11 |
0 |
0 |
0 |
||||
|
111 |
00 |
1 |
|
0 |
p |
1 |
|
|
01 |
1 |
1 |
1 |
||||
|
10 |
0 |
0 |
0 |
||||
|
11 |
0 |
1 |
0 |
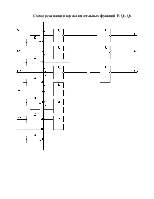
Схема реализации модуля ОЧС на мультиплексорах
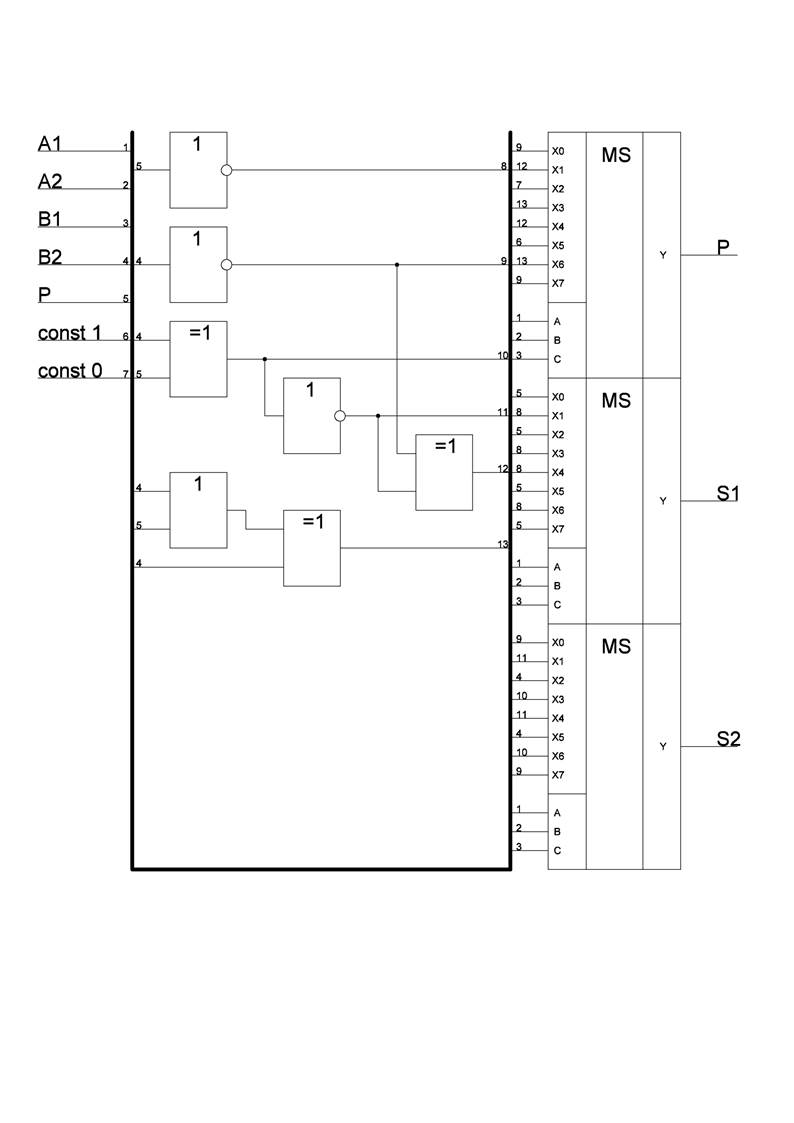
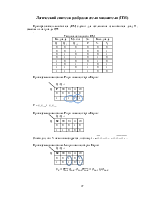
Преобразователь множителя (ПМ) служит для исключения из множителя диад
11, заменяя их на триады 
.
Таблица истинности ПМ.
|
Вх. диада |
Мл. бит |
Зн. |
Вых. диада |
||
|
Qn |
Qn-1 |
Qn-2 |
P |
S1 |
S2 |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
0 |
0 |
Проведём минимизацию P при помощи карты Карно:
|
Qn-1Qn-2 |
|||||
|
Qn |
P |
00 |
01 |
11 |
10 |
|
0 |
|
0 |
|
0 |
|
|
1 |
1 |
1 |
1 |
||
P = 
+
Проведём минимизацию P при помощи карты Карно:
|
Qn-1Qn-2 |
|||||
|
Qn |
S2 |
00 |
01 |
11 |
10 |
|
0 |
0 |
0 |
1 |
0 |
|
|
1 |
1 |
0 |
0 |
0 |
|
Очевидно, что S1 не минимизируется,
поэтому 
.
Проведём минимизацию S2 при помощи карты Карно:
|
Qn-1Qn-2 |
|||||
|
Qn |
S2 |
00 |
01 |
11 |
10 |
|
0 |
|
1 |
|
1 |
|
|
1 |
0 |
1 |
0 |
1 |
|
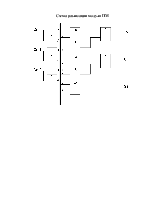
Схема реализации модуля ПМ
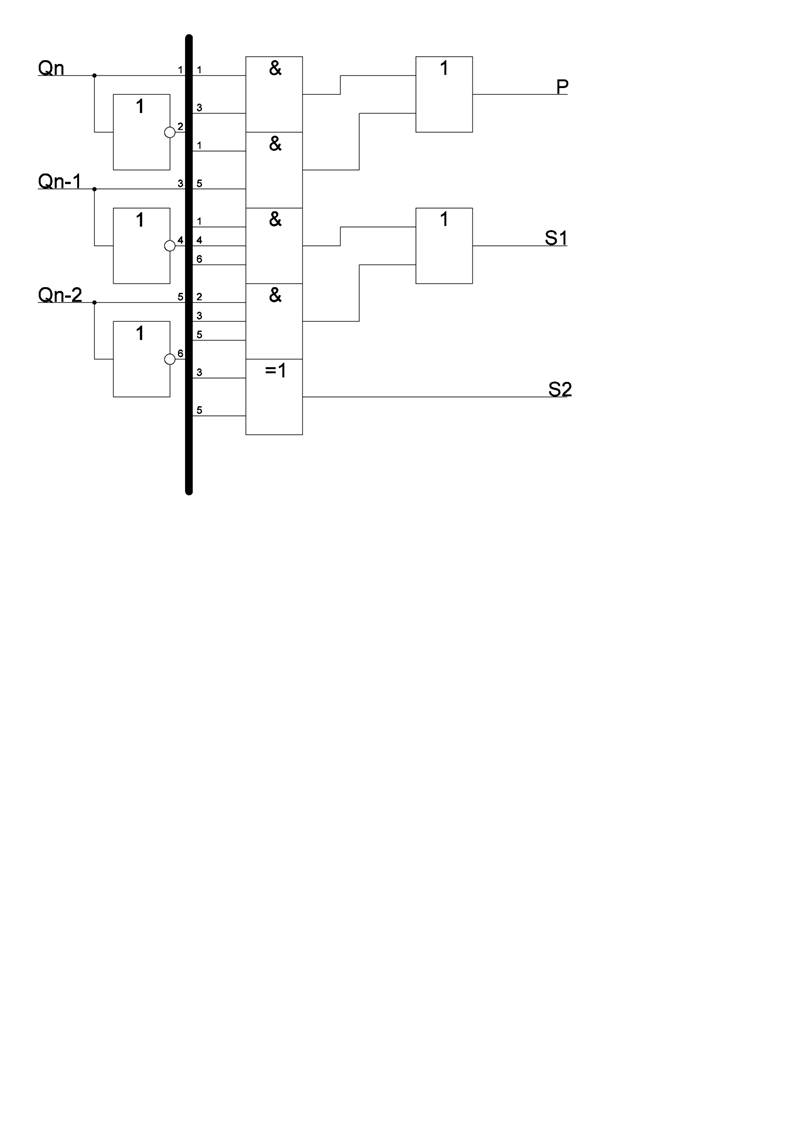
1. Лысиков Б.Г. Арифметические и логические основы цифровых автоматов. Мн.: Вышейшая школа, 1980.
2. Лысиков Б.Г. Цифровая вычислительная техника. Мн.: , 2003 г.
3. Луцик Ю.А., Лукьянова И.В.– Учебное пособие по курсу "Арифметические и логические основы вычислительной техники". -Мн.: ротапринт МРТИ, 2004 г.
4. Луцик Ю.А., Лукьянова И.В. -- Методические указания к курсовому проекту по курсу “Арифметические
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
0
0
0