







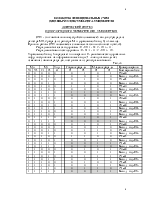








Минимизацию данной функции проведем при помощи карт Карно-Вейча.
L = {10001, 10010, 10011, 10101, 11001, 11010, 11011, 11101}.
______ X2 ______
|
X1 |
1 |
1 |
1 |
1 |
1 |
1 |
Y1 |
||
|
1 |
* |
* |
* |
* |
1 |
||||
|
* |
* |
* |
* |
||||||
___________________________
_____________ Y2 _____________
H H
Минимальная форма функции выхода Р3 будет такова:
Сmin = { 1XXX1, 1XX1X }
b
P3 =X1H +X1Y2 ;
К = (8*5 + 8 + 4) / (4+2) = 8,667.
Множество единичных кубов для выходов P4:
Результаты умножения Ci * Ci приведены в таблицах 4.1, 4.2, 4.3, 4.4.
Z0 = Æ;
Z1 = Æ;
Z2 = {0XX00, XX000, 0X1X0};
Z3 = {X10XX, 01XXX, X1XX1, X1X1X, XX11X}.
Z = {0XX00, XX000, 0X1X0, X10XX, 01XXX, X1XX1, X1X1X, XX11X }
По результатам вычитания Z # (Z \ z) не все кубы множества Z являются обязательными (см. табл. 4.5).
Для выявления кубов, покрывающих вершины не принадлежащие к комплексу L, используется операция пересечения множеств. Пересечение множества L с остатками, полученными при выделении L-экстремалей, показывает, содержат ли остатки единичные кубы, т.е. нужен нам этот куб или нет. (табл. 4.6) После проведенной операции L – экстремалями являются кубы {XX000, X1XX1}. Zk = {0XX00, 0X1X0, X10XX, 01XXX, X1X1X, XX11X}.
Найдем множество L2, используя операцию вычитания (см. табл. 4.7). L2 = {00100, 01010, 01100, 11010}.
Проведем операцию пересечения множества L2 с множеством Zk (см. табл. 4.8). В результате всех проведенных действий получим несколько тупиковых форм:
Сmin1 = {0X1X0, X1X1X, XX000, X1XX1}
Сmin 2= {0X1X0, X10XX, XX000, X1XX1}.
Сmin 3= {0XX00, X10XX, XX000, X1XX1}.
Сmin 4= {0XX00, X1X1X, XX000, X1XX1}.
Выберем одну из них:
Сmin1 = {0X1X0, X1X1X, XX000, X1XX1}
b
P4=X1 Y1 H + X2 Y2 + Y1 Y2 H + X2 H
К = (14*5 +1 4 + 5) / (10 + 4 + 4) = 4,944.
Для реализации полученных минимальных функций в заданном базисе ИЛИ-НЕ используем правила де Моргана.
E b
P1 = X2 Y1 H
E b
P2 = H
P3 = X1 H + X1 Y2 =
P4 = X1Y1 H + X2 Y2 + Y1 Y2 H + X2 H
Функциональная схема блока ОЧУ приведена на рис. 4.
ОДНОРАЗРЯДНОГО ЧЕТВЕРИЧНОГО СУММАТОРА
ОЧС - это комбинационное устройство, имеющее 5 входов (2 разряда одного слагаемого, 2 разряда второго слагаемого и вход переноса) и 3 выхода. Принцип работы ОЧС описывается с помощью таблицы истинности (табл.21).
Разряды обоих слагаемых закодированы: 0 - 11; 1 - 00; 2 - 01; 3 - 10.
Табл. 21
|
А1 |
А2 |
В1 |
В2 |
p |
П |
S1 |
S2 |
Пример операции в четверичной с/с |
||
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
2+2+0=10 |
* |
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
2+2+1=11 |
* |
|
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
2+0+0=02 |
||
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
2+0+1=03 |
||
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
2+3+0=11 |
* |
|
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
2+3+1=12 |
* |
|
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
2+1+0=03 |
||
|
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
2+1+1=10 |
||
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0+2+0=02 |
* |
|
|
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0+2+1=03 |
* |
|
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0+0+0=00 |
||
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0+0+1=01 |
||
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0+3+0=03 |
* |
|
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0+3+1=10 |
* |
|
|
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0+1+0=01 |
||
|
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0+1+1=02 |
||
|
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
3+2+0=11 |
* |
|
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
3+2+1=12 |
* |
|
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
3+0+0=03 |
||
|
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
3+0+1=10 |
||
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
3+3+0=12 |
* |
|
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
3+3+1=13 |
* |
|
|
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
3+1+0=10 |
||
|
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
3+1+1=11 |
||
|
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1+2+0=03 |
* |
|
|
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1+2+1=10 |
* |
|
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1+0+0=01 |
||
|
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1+0+1=02 |
||
|
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1+3+0=10 |
* |
|
|
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1+3+1=11 |
* |
|
|
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1+1+0=02 |
||
|
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1+1+1=03 |
||
Так как ОЧС синтезируется для схемы 1-го типа, то в таблице истинности присутствуют 16 безразличных наборов, т.к. со старших выходов ОЧУ не могут прийти коды 2 и 3.
Минимизация выходов проводится с помощью карт Карно-Вейча.
Для выхода П:
______ A2 ______
|
A1 |
* |
* |
1 |
* |
* |
B1 |
|||
|
* |
* |
1 |
1 |
* |
* |
||||
|
* |
* |
1 |
* |
* |
|||||
|
* |
* |
* |
* |
___________________________
_____________ B2 _____________
p p
__ _ _
Пmin= A2 B1 P + A1 A2 P + A1 A2 B1;
Эффективность минимизации можно оценить отношением числа входов схемы (цены схемы) до и после минимизации:
К = (4*5 + 4 + 4) / (9 + 3 + 1) = 2,1538;
Для выхода S1:
______ A2 ______
|
A1 |
* |
* |
1 |
1 |
* |
* |
B1 |
||
|
* |
* |
1 |
1 |
* |
* |
||||
|
* |
* |
1 |
1 |
* |
* |
||||
|
* |
* |
1 |
1 |
* |
* |
___________________________
_____________ B2 _____________
p p
В результате имеем:
_ e
S1min =A1 B1 P + A1 B1 P + A1 B1 P + A1 B1 P.
Коэффициент минимизации для S1min:
К = (8*5 + 8 + 4) / (4*3 + 4 + 3) = 2,737;
Для выхода S2:
______ A2 ______
|
A1 |
* |
* |
1 |
1 |
* |
* |
B1 |
||
|
* |
* |
1 |
1 |
* |
* |
||||
|
* |
* |
1 |
1 |
* |
* |
||||
|
* |
* |
1 |
1 |
* |
* |
___________________________
_____________ B2 _____________
p p
e
Smin = A1 A2 B1 + A1 A2 P + A2 B1 P + A1 A2 P + A1 A2 B1 + A2 B1 P ;
Коэффициент минимизации для S2:
К = (8*5 + 8 + 4) / (18 + 6 + 4) = 1,857.
Мультиплексор – это логическая схема, имеющая n информационных входов, m управляющих входов и один выход. При этом должно выполняться условие n = 2m.
На выход мультиплексора может быть пропущен без изменений любой (один) логический сигнал, поступающий на информационные входы. Порядковый номер информационного входа, значение с которого в данный момент должно быть передано на выход, определяется двоичным кодом на управляющих входах.
Для реализации наших функций используем мультиплексоры 1 из 8.
Входные данные разбиваются на группы с одинаковыми значениями определенных входных переменных, например, A1, A2 и B1, которые используются в качестве адресозадающих. На соответствующие информационные входы подается значение функции, зависящее только от значений остальных (не адресозадающих) входных переменных и верное для определенного набора значений адресных переменных.
Реализация ОЧС с учетом безразличных наборов приведена на рис. 5.
Реализация ОЧС в нашем логическом базисе приведена на рис. 6.
ЛОГИЧЕСКИЙ СИНТЕЗ ПРЕОБРАЗОВАТЕЛЯ МНОЖИТЕЛЯ (ПМ)
Задачей ПМ является исключение из множителя диады 11 путем замены их на триады 101, при этом единица переноса будет добавлена по цепи обратной связи к следующей диаде множителя (см. выход П ). Выход О ПМ переходит в единичное состояние, если текущая диада содержит отрицание. Принцип работы ПМ описывается в табл. 22.
Табл. 5
|
D1 |
D2 |
D3 |
П1 |
П2 |
O |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
1 |
0 |
1 |
0 |
|
|
0 |
1 |
0 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
0 |
0 |
|
|
1 |
0 |
0 |
1 |
0 |
1 |
|
|
1 |
0 |
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
0 |
1 |
1 |
|
|
1 |
1 |
1 |
0 |
0 |
0 |
0 = D1 D3 + D1 D2
П1 = D1 D2 D3 + D1 D2 D3
П2 = D2 D3 + D2 D3
ПМ реализуется в нашем элементарном логическом базисе и привлекателен простотой способа реализации. Реализация ПМ приведена на рис.7.
В общую сумму времени, требуемого для умножения на один разряд множителя, входят следующие составляющие:
tСДВ - время сдвига множителя и частичной суммы на один четверичный разряд.
tПМ - время преобразования двоичной диады множителя.
tФДК - время формирования дополнительного кода множимого требуемого знака.
tОЧУ - время умножения одной диады множимого на текущую диаду множителя. В общую сумму входит лишь один раз, т. к. умножение всех двоичных пар множимого происходит одновременно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.