Информатика и выч. техника \ Арифметические и логические основы вычислительной техники

Синтез устройства умножения двоично-четверичных чисел в дополнительных кодах (исходные операнды - дробные десятичные числа: Мн = -19,88; Мт = 45,77; алгоритм выполнения операции умножения: А)

Страницы работы

27 страниц (Word-файл)
Посмотреть все страницы
Скачать файл

Уважаемые коллеги! Предлагаем вам разработку программного обеспечения под ключ.

Опытные программисты сделают для вас мобильное приложение, нейронную сеть, систему искусственного интеллекта, SaaS-сервис, производственную систему, внедрят или разработают ERP/CRM, запустят стартап.

Сферы - промышленность, ритейл, производственные компании, стартапы, финансы и другие направления.

Языки программирования: Java, PHP, Ruby, C++, .NET, Python, Go, Kotlin, Swift, React Native, Flutter и многие другие.

Всегда на связи. Соблюдаем сроки. Предложим адекватную конкурентную цену.

Заходите к нам на сайт и пишите, с удовольствием вам во всем поможем.

Фрагмент текста работы

Первым шагом алгоритма Рота является нахождение множества простых импликант. Умножение C0*C0 приведет в таблице 11. В результате  этой операции мы получили новое множество кубов C1:

 


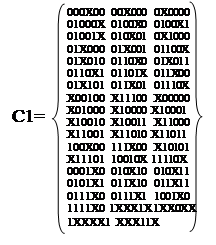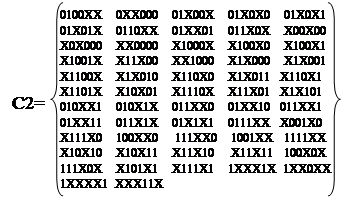Множество Z0 кубов пустое. Следующее умножение C1*C1 приведено в таблице 12. В результате получили новое множество кубов C2:

Множество Z1 кубов пустое. Следующее умножение C2*C2 приведено в таблице 13. В результате получили новое множество кубов C3:

 


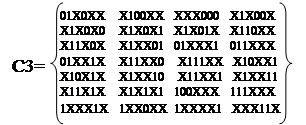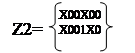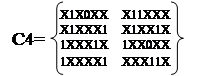Во множестве Z2 содержится 2 куба, которые не дали кубов большей размерности при выполнении операции C2C2 . Умножение C3*C3 приведено в таблице 14. В результате получили новое множество кубов C4:

 


Таблица 15. Умножение C4*C4

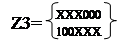X1X0XX

X11XXX

X1XXX1

X1XX1X

1XXX1X

1XX0XX

1XXXX1

XXX11X

X1X0XX

X11XXX

X110XX

X1XXX1

X1X0X1

X11XX1

X1XX1X

X1X01X

X11X1X

X1XX11

1XXX1X

11X01X

111X1X

11XX11

11XX1X

1XX0XX

11X0XX

1110XX

11X0X1

11X01X

1XX01X

1XXXX1

11X0X1

111XX1

11XXX1

11XX11

1XXX11

1XX0X1

XXX1XX

X1XY1X

X1111X

X1X111

X1X11X

1XX11X

1XXY1X

1XX111

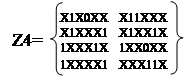
В результате С4*С4 новых кубов не образуется. Таким образом, в результате проведенных операций мы сформировали множество простых импликант Z=Z0UZ1UZ2UZ3UZ4 .

Следующий этап  - поиск L – экстремалей на множестве простых импликант, приведено в  таблице 16.

Таблица 16. Поиск L-экстремалей 

X00X00

X001X0

XXX000

100XXX

X1X0XX

X11XXX

X1XXX1

X1XX1X

1XXX1X

1XX0XX

1XXXX1

XXX11X

X00X00

ZZZZ1Z

X00110

Z11ZZZ

X1X000

XX1000

ZZZZ11

100X1X

100XX1

ZY1Z11

X1X0XX

ZYYZ11

X11XXX

ZY1ZY1

X1XXX1

ZY1ZY1

X1XX1X

Z11ZY1

1XXX1X

Z11Z11

11X0XX

1X10XX

1XX01X

1XX0X1

Z11Z11

1XXXX1

Z11ZY1

XXX11X

X001X0

ZZZ0ZZ

X00000

ZY1YZZ

X1X000

Z1YYZZ

XX1000

ZZZ0Z1

10001X

100X11

ZZZ0ZY

100XX1

ZY1YZ1

X1X0XX

ZYY0Z1

X11XXX

ZY10ZY

X1XXX1

ZY10Z1

X1XX1X

Z110Z1

11XX1X

1X1X1X

1XX01X

1XXX11

ZY1YZ1

11X0XX

Z1YYZ1

1X10XX

Z11YZ1

1XX01X

Z11YZY

1XX0X1

Z110ZY

1XXXX1

Z11ZZ1

X1X11X

XX111X

XXX111

XXX000

ZZZZZZ

ZZZYYZ

X00110

ZZZZY1

10001X

ZZZ1YY

100X11

ZZZ11Y

100XX1

ZZZZ11

X1X01X

X1X0X1

ZZZ111

X111XX

X11X1X

X11XX1

ZZZ11Y

X1XXX1

ZZZ1Y1

X1XX1X

ZZZ1Y1

11XX1X

ZZZ1Y1

1X1X1X

ZZZZY1

1XX01X

ZZZ1YY

1XXX11

ZZZZ11

11X01X

11X0X1

ZZZZ11

1X101X

1X10X1

ZZZZY1

1XXX01X

ZZZZ1Y

1XX0X1

ZZZ11Y

1XXXX1

ZZZYY1

X1X11X

ZZZYY1

XX111X

ZZZYYY

XXX111

100XXX

0ZZZZZ

000110

0Y1ZZZ

X1X000

01YZZZ

XX1000

0Y1ZZZ

X1X01X

0Y1ZZZ

X1X0X1

0YYZZZ

X111XX

0YYZZZ

X11X1X

0YYZZZ

X11XX1

0Y1ZZZZ

X1XXX1

0Y1ZZZ

X1XX1X

ZY1ZZZ

11XX1X

Z1YZZZ

1X1X1X

Z11ZZZ

11X01X

1X101X

Z11ZZZ

11XX11

1X1X11

ZY1ZZZ

11X01X

ZY1ZZZ

11X0X1

Z1YZZZ

1X101X

Z1YZZZ

1X10X1

Z11ZZZ

11X01X

1X101X

Z11ZZZ

11X0X1

1X10X1

Z11ZZZ

11XXX1

1X1XX1

0Y1ZZZ

X1X11X

01YZZZ

XX111X

011ZZZ

0XX111

X1X111

XX1111

X1X0XX

ZYZYZZ

000110

ZZZZZZ

Z0ZZZZ

X01000

ZYZZZZ

10001X

ZYZ1ZZ

100X11

ZYZ1ZZ

100XX1

ZZZYZZ

X111XX

ZZZ1ZZ

X1111X

ZZZ1ZZ

X111X1

ZZZ1ZZ

X1X1X1

ZZZ1ZZ

X1X11X

ZZZ1ZZ

11X11X

Z0Z1ZZ

101X1X

1X111X

ZZZZZZ

Z0ZZZZ

10101X

ZZZ1ZZ

11X111

Z0Z1ZZ

101X11

1X1111

ZZZZZZ

ZZZZZZ

Z0ZZZZ

10101X

Z0ZZZZ

1010X1

ZZZZZZ

Z0ZZZZ

10101X

ZZZZZZ

Z0ZZZZ

1010X1

ZZZ1ZZ

11X1X1

Z0Z1ZZ

101XX1

1X11X1

ZZZYZZ

X1X11X

Z0ZYZZ

XX111X

Z0ZYZZ

0XX111

ZZZYZZ

X1X111

Z0ZYZZ

XX1111

X11XXX

ZYYZZZ

000110

ZYZZZ

X01000

ZYYZZZ

10001X

ZYYZZZ

100X11

ZTTZZZ

100XX1

ZZ0ZZZ

X1001X

ZZ0ZZZ

X100X1

ZZ0ZZZ

X101X1

ZZ0ZZZ

X1011X

ZZ0ZZZ

11011X

ZYZZZZ

101X1X

Z0ZZZZ

10111X

ZYZZZZ

10101X

ZZ0ZZZ

110111

ZYZZZZ

101X11

Z0ZZZZ

101111

ZYZZZZ

10101Z

ZYZZZZ

1010X1

ZYZZZZ

10101X

ZYZZZZ

1010X1

ZZ0ZZZ

1101X1

ZYZZZZ

101XX1

Z0ZZZZ

1011X1

ZZ0ZZZ

X1011X

Z0ZZZZ

X0111X

Z00ZZZ

00X111

0X0111

ZZ0ZZZ

X10111

Z0ZZZZ

X01111

X11XXX

ZYYZZZ

000110

ZYZZZZ

X01000

ZYYZZZ

10001X

ZYYZZZ

100X11

ZYYZZZ

100XX1

ZZ0ZZZ

X1001X

ZZ0ZZZ

X100X1

ZZ0ZZZ

X101X1

ZZ0ZZZ

Z1011X

ZZ0ZZZ

11011X

ZYZZZZ

101X1X

Z0ZZZZ

10111X

ZYZZZZ

10101X

ZZ0ZZZ

110111

ZYZZZZ

101X11

Z0ZZZZ

101111

ZYZZZZ

10101X

ZYZZZZ

1010X1

ZYZZZZ

10101X

ZYZZZZ

1010X1

ZZ0ZZZ

1101X1

ZYZZZZ

101XX1

Z0ZZZZ

1011X1

Z0ZZZ

X1011X

Z0ZZZZ

X0111X

Z00ZZZ

00X111

0X0111

ZZ0ZZZ

X10111

Z0ZZZZ

X01111

X1XXX1

ZYZZZY

000110

ZYZZZY

X01000

ZYZZZ0

10001X

ZYZZZZ

100X11

ZYZZZZ

100XX1

ZZZZZ0

X10010

ZZZZZZ

ZZZZZ0

X111X0

ZZZZZ0

X11110

ZZZZZZ

ZZZZZ0

X10110

ZZZZZ0

110110

ZYZZZ0

101X1X

ZYZZZ0

10111X

ZYZZZ0

10101X

ZZZZZZ

ZYZZZZ

101X11

ZYZZZZ

101111

ZYZZZ0

10101X

ZYZZZZ

1010X1

ZYZZZ0

10101X

ZYZZZZ

1010X1

ZZZZZZ

ZYZZZZ

101XX1

ZYZZZZ

1011X1

ZZZZZ0

X10110

ZYZZZ0

X0111X

ZYZZZZ

00X111

Z0ZZZZ

000111

ZZZZZZ

ZYZZZZ

X01111

X1XX1X

ZYZZZZ

000110

ZYZZYZ

X01000

ZYZZZZ

10001X

ZYZZZZ

1001X11

ZYZZ0Z

100XX1

ZZZZZZ

ZZZZ0Z

X11100

ZZZZZZ

ZZZZ0Z

X10101

ZZZZZZ

ZYZZZZ

101X1X

ZYZZZZ

10111X

ZYZZZZ

10101X

ZYZZZZ

101X11

ZYZZZZ

101111

ZYZZZZ

10101X

ZYZZ0Z

1010X1

ZYZZZZ

10101X

ZYZZ0Z

1010X1

ZYZZ0Z

101XX1

ZYZZ0Z

1011X1

ZZZZZZ

ZYZZZZ

X0111X

ZYZZZZ

00X111

ZYZZZZ

000111

ZYZZZZ

X01111

1XXX1X

YZZZZZ

000110

0ZZZYZ

X01000

ZZZZZZ

ZZZZZZ

ZZZZ0Z

100X01

0ZZZYZ

X11100

0ZZZYZ

X10101

0ZZZZZ

010110

ZZZZZZ

ZZZZ0Z

101001

ZZZZZZ

ZZZZ0Z

101001

ZZZZ0Z

101X01

ZZZZ0Z

101101

0ZZZZZ

00111X

YZZZZZ

00X111

YZZZZZ

000111

0ZZZZZ

001111

1XX0XX

YZZYZZ

000110

0ZZZZZ

00100

ZZZ1ZZ

100101

0ZZYZZ

X11100

0ZZYZZ

X10101

YZZYZZ

010110

ZZZ1ZZ

10111X

ZZZYZZ

10111X

ZZZZZZ

ZZZ1ZZ

101111

ZZZYZZ

101111

ZZZ1ZZ

101101

ZZZYZZ

101101

YZZYZZ

00111X

YZZYZZ

00X111

YZZYZZ

000111

YZZYZZ

001111

1XXXX1

YZZZZY

000110

YZZZZY

001000

ZZZZZZ

0ZZZZY

X11100

0ZZZZZ

010101

YZZZZY

010110

ZZZZZ0

101110

ZZZZZ0

101110

ZZZZZZ

ZZZZZZ

ZZZZZZ

ZZZZZZ

YZZZZ0

00111X

YZZZZZ

00X111

YZZZZZ

000111

YZZZZZ

001111

XXX11X

ZZZZZZ

ZZZYYZ

001000

ZZZZZYZ

X11100

ZZZZYZ

010101

ZZZZZZ

ZZZZZZ

ZZZZZZ

ZZZZYZ

101101

ZZZZYZ

101101

001000

X11100

010101

101101

00111X

00X111

В результате этой операции L – экстремалями стали  простые импликанты: XXX000, X11XXX, X1XXX1, 1XXXX1, XXX11X.

По результатам таблицы 17, L – экстремалями не связанными с безразличными наборами стали кубы XXX000, X11XXX, X1XXX1. Далее необходимо проанализировать, какие из исходных единичных кубов (множество L) не покрыты найденными L – экстремалями. Данный анализ приведен в таблице 1.

Таблица 17. Проверка L-экстремалей.

001000

X11100

010101

101101

00111X

00X111

000111

001111

000000

00Z000

0ZZZ00

0Z0Z0Z

Z0ZZ0Z

00ZZZ0

000ZZZ

000ZZZ

00ZZZZ

000100

00ZZ00

0ZZ100

0Z010Z

Z0Z10Z

00Z1Z0

0001ZZ

0001ZZ

00Z1ZZ

001000

001000

0Z1Z00

0ZZZ0Z

Z01Z0Z

001ZZ0

001ZZZ

00ZZZZ

001ZZZ

010000

0ZZ000

01ZZ00

010Z0Z

ZZZZ0Z

0ZZZZ0

0Z0ZZZ

0Z0ZZZ

0ZZZZZ

010001

0ZZ00Z

01ZZ0Z

010Z01

ZZZZ01

0ZZZZ1

0Z0ZZ1

0Z0ZZ1

0ZZZZ1

010010

0ZZ0Z0

01ZZZ0

010ZZZ

ZZZZZZ

0ZZZ10

0Z0Z1Z

0Z0Z1Z

0ZZZ1Z

010011

0ZZ0ZZ

01ZZZZ

010ZZ1

ZZZZZ1

0ZZZ11

0Z0Z11

0Z0Z11

0ZZZ11

010101

0ZZZ0Z

01Z10Z

010101

ZZZ101

0ZZ1Z1

0Z01Z1

0Z01Z1

0ZZ1Z1

011000

0Z1000

011Z00

01ZZ0Z

ZZ1Z0Z

0Z1ZZ0

0Z1ZZZ

0ZZZZZ

0Z1ZZZ

011001

0Z100Z

011Z0Z

01ZZ01

ZZ1Z01

0Z1ZZ1

0Z1ZZ1

0ZZZZ1

0Z1ZZ1

011010

0Z10Z0

011ZZ0

01ZZZZ

ZZ1ZZZ

0Z1Z10

0Z1Z1Z

0ZZZ1Z

0Z1Z1Z

011011

0Z10ZZ

011ZZZ

01ZZZ1

ZZ1ZZ1

0Z1Z11

0Z1Z11

0ZZZ11

0Z1Z11

011100

0Z1Z00

011100

01Z10Z

ZZ110Z

0Z11Z0

0Z11ZZ

0ZZ1ZZ

0Z11ZZ

011101

0Z1Z0Z

01110Z

01Z101

ZZ1101

0Z11Z1

0Z11Z1

0ZZ1Z1

0Z11Z1

100100

Z0ZZ00

1ZZ100

ZZ010Z

10Z10Z

Z0Z1Z0

Z001ZZ

Z001ZZ

Z0Z1ZZ

111100

ZZ1Z00

111100

Z1Z10Z

1Z110Z

ZZ11Z0

ZZ11ZZ

ZZZ1ZZ

ZZ11ZZ

Далее необходимо проанализировать, какие из исходных единичных кубов (множество L) не покрыты найденными L – экстремалями. Данный анализ приведен в таблице 18.

Таблица 18. Поиск непокрытых исходных наборов.

000000

000100

001000

010000

010001

010010

010011

010101

011000

011001

011010

011011

011100

011101

100100

111100

XXX000

ZZZZZZ

ZZZYZZ

000100

ZZZZZZ

ZZZZZZ

ZZZZZY

010001

ZZZZYZ

010010

ZZZZYY

010011

ZZZYZY

010101

ZZZZZZ

ZZZZZY

011001

ZZZZYZ

011010

ZZZZYY

011011

ZZZYZZ

011100

ZZZYZY

011101

ZZZYZ

100100

ZZZYZZ

111100

X11XXX

ZYYZZZ

000100

ZZYZZZ

010001

ZZYZZZ

010010

ZZYZZZ

010011

ZZYZZZ

010101

ZZZZZZ

ZZZZZZ

ZZZZZZ

ZZZZZZ

ZZZZZZ

ZYYZZZ

100100

ZZZZZZ

X1XXX1

ZYZZZY

000100

ZZZZZZ

ZZZZZY

010010

ZZZZZZ

ZZZZZZ

ZYZZZY

100100

000100

010010

100100

Из таблицы 16 видно, что L – экстремалями не покрыты следующие единичные кубы:  000100, 010010, 100100. Чтобы покрыть их воспользуемся множеством простых импликант, не ставших L – экстремалями.

Таблица 19.Поиск покрытия оставшихся кубов

000100

010010

100100

X00X00

000100

0Z00Z0

100100

X001X0

000100

0Z0Z10

100100

100XXX

Z00100

ZZ0010

100100

X1X0XX

0Z0Z00

010010

1Z0Z00

X1XX1X

0Z01Z0

010010

1Z01Z0

1XXX1X

Z001Z0

Z10010

1001Z0

1XX0XX

Z00Z00

Z10010

100Z00

1XXXX1

Z0010Z

Z1001Z

10010Z

XXX11X

0001Z0

010Z10

1001Z0

Из таблицы видно, что для покрытия оставшихся единичных кубов можно взять следующие простые импликанты X00X00, X1XX1X;

Следовательно, возможно одна из тупиковых минимальных форм:

 


Q1min = Y1Y2h + X1X2 + X1h + X1X2Y2h+X1Y2

Эффективность минимизации:

K = (16*5+5+16)/23=4.4

Минимизация выхода Q2.

Определим множества единичных кубов L и множество безразличных кубов N:

 


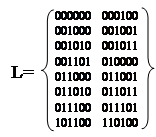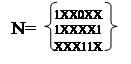Сформируем множество C0 = L U N.

Первым шагом алгоритма Рота является нахождение множества простых импликант. Умножение C0*C0 приведет в таблице 20.

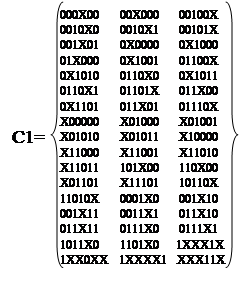В результате  этой операции мы получили новое множество кубов C1:

Множество Z0 кубов, не участвовавших в образовании новых кубов, пустое. Следующее умножение C1*C1 приведено в таблице 21. В результате получили новое множество кубов C2:

 


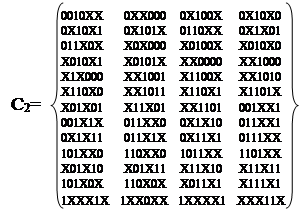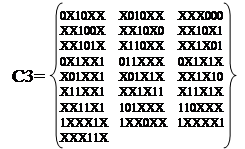Множество Z1 кубов пустое. Следующее умножение C2*C2 приведено в таблице 22. В результате получили новое множество кубов C3:

 


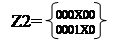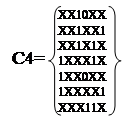Во множестве Z2 содержится 2 куба, которые не дали кубов большей размерности при выполнении операции C2*C2.  Умножение C3*C3 приведено в таблице 23. В результате получили новое множество кубов C4:

 


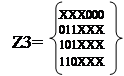Умножение C4*C4 приведено в таблице 24. В результате новых кубов не образуется. Таким образом, в результате проведенных операций мы сформировали множество простых импликант Z=Z0UZ1UZ2UZ3;

 


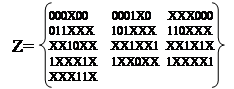Таблица 24. С4*С4

XX10XX

XX1XX1

XX1X1X

1XXX1X

1XX0XX

1XXXX1

XX10XX

XX1XX1

XX10X1

XX1X1X

XX101X

XX1X11

1XXX1X

1X101X

1X1X11

1X1X1X

1XX0XX

1X10XX

1X10X1

1X101X

1XX01X

1XXXX1

1X10X1

1X1XX1

1X1X11

1XXX11

1XX0X1

111XX1

11XY1X

XX1111

XX111X

1XX11X

1XXY1X

1XX111

Следующий этап  - поиск L – экстремалей на множестве простых импликант. Для этого используется операция # (вычитание) таблица 25.

Таблица 26. Проверка L – экстремалей.

010000

011100

101100

110100

001101

1100101

01011X

000111

0X0111

000000

0Z0000

0ZZZ00

Z0ZZ00

Z0ZZ00

00ZZ0Z

Z00Z0Z

0Z0ZZ0

000ZZZ

000ZZZ

000100

0Z0Z00

0ZZ100

Z0Z100

Z0Z100

00Z10Z

Z0010Z

0Z01Z0

0001ZZ

0001ZZ

001000

0ZZ000

0Z1Z00

Z01Z00

ZZZZ00

001Z0Z

Z0ZZ0Z

0ZZZZ0

00ZZZZ

00ZZZZ

001001

0ZZ00Z

0Z1Z0Z

Z01Z0Z

ZZZZ0Z

001Z01

Z0ZZ01

0ZZZZ1

00ZZZ1

00ZZZ1

001010

0ZZ0Z0

0Z1ZZ0

Z01ZZ0

ZZZZZ0

001ZZZ

Z0ZZZZ

0ZZZ10

00ZZ1Z

00ZZ1Z

001011

0ZZ0ZZ

0Z1ZZZ

Z01ZZZ

ZZZZZZ

001ZZ1

Z0ZZZ1

0ZZZ11

00ZZ11

00ZZ11

001101

0ZZZ0Z

0Z110Z

Z0110Z

ZZZ10Z

001101

Z0Z101

0ZZ1Z1

00Z1Z1

00Z1Z1

010000

010000

01ZZ00

ZZZZ00

Z10Z00

0ZZZ0Z

ZZ0Z0Z

010ZZ0

0Z0ZZZ

010ZZZ

011000

01Z000

011Z00

ZZ1Z00

ZZ1Z00

0Z1Z0Z

ZZZZ0Z

01ZZZ0

0ZZZZZ

01ZZZZ

011001

01Z00Z

011Z0Z

ZZ1Z0Z

ZZ1Z0Z

Z1ZZ01

ZZZZ01

01ZZZ1

0ZZZZ1

01ZZZ1

011010

01Z0Z0

011ZZ0

ZZ1ZZ0

ZZ1ZZ0

0Z1ZZZ

ZZZZZZ

01ZZ10

0ZZZ1Z

01ZZ1Z

011011

01Z0ZZ

011ZZZ

ZZ1ZZZ

Z1ZZZZ

0Z1ZZ1

ZZZZZ1

01ZZ11

0ZZZ11

01ZZ11

011100

01ZZ00

011100

ZZ1100

Z1Z100

0Z110Z

ZZZ10Z

01Z1Z0

0ZZ1ZZ

01Z1ZZ

011101

01ZZ0Z

01110Z

ZZ110Z

Z1Z10Z

0Z1101

ZZZ101

01Z1Z1

0ZZ1Z1

01Z1Z1

101100

ZZZZ00

ZZ1100

101100

1ZZ100

Z0110Z

10Z10Z

ZZZ1Z0

Z0Z1ZZ

Z0Z1ZZ

110100

Z10Z00

Z1Z100

1ZZ100

110100

ZZZ10Z

1Z010Z

Z101Z0

ZZ01ZZ

Z101ZZ

В результате L – экстремалями стали  простые импликанты: XXX000; 011XXX; 101XXX; 110XXX; XX1XX1. Далее необходимо проанализировать, какие из исходных единичных кубов (множество L) не покрыты найденными L – экстремалями. Данный анализ приведен в таблице 27.

Таблица 27. Поиск непокрытых исходных наборов. L/E

000000

000100

001000

001001

001010

001011

001101

010000

011000

011001

011010

011011

011100

011101

101100

110100

XXX000

ZZZZZZ

ZZZYZZ

000100

ZZZZZZ

ZZZZZY

001001

ZZZZYZ

001010

ZZZZYY

001011

ZZZYZY

001101

ZZZZZZ

ZZZZZZ

ZZZZZY

011001

ZZZZYZ

011010

ZZZZYY

011011

ZZZYZZ

011100

ZZZYZY

011101

ZZZYZZ

101100

ZZZYZZ

110100

011XXX

ZYYZZZ

000100

ZYZZZZ

001001

ZYZZZZ

001010

ZYZZZZ

001011

ZYZZZZ

001101

ZZZZZZ

ZZZZZZ

ZZZZZZ

ZZZZZZ

ZZZZZZ

YYZZZZ

101100

YZYZZZ

110100

101XXX

YZYZZZ

000100

YZZZZZ

001001

YZZZZZ

001010

YZZZZZ

001011

YZZZZZ

001101

ZZZZZZ

ZYYZZZ

110100

110XXX

YYZZZZ

000100

YYYZZZ

001001

YYYZZZ

001010

YYYZZZ

001011

YYYZZZ

001101

ZZZZZZ

XX1XX1

ZZYZZY

00100

ZZZZZZ

ZZZZZY

001010

ZZZZZZ

ZZZZZZ

000100

001010

Из таблицы видно, что L – экстремалями не покрыты кубы 000100 и 001010. Чтобы покрыть их воспользуемся множеством простых импликант, не ставших L – экстремалями.

Таблица 28. Покрытие оставшихся наборов.

000100

001010

000X00

000100

00Z0Z0

0001X0

000100

00ZZ10

XX10XX

00ZZ00

001010

XX1X1X

00Z1Z0

001010

1XXX1X

Z001Z0

Z01010

1XX0XX

Z00Z00

Z01010

1XXXX1

Z0010Z

Z0101Z

XXX11X

0001Z0

001Z10

Из таблицы 28 видно, что для покрытия оставшихся единичных кубов можно взять следующие простые импликанты 0001X0, XX1Х1Х.

Следовательно, существует одна тупиковая минимальная форма:

Q2=P1X1X2Y1h+X2Y2+Y1Y2h+P1X1X2+P1X1X2+P1X1X2+X2h.

Эффективность минимизации:

К=(16*5+5+16)/34=3.0

5.3. Логический синтез ОЧC на мультиплексорах

A1

A2

B1

П
S1

S2

0

0

0

1

B2P+B2

B2P

0

0

1

B2P

B2P

P

0

1

0

1

B2

B2P+B2P

0

1

1

B2+B2P

B2+B2P

P+B2P

1

0

0
B2P+B2

B2P+B2

B2P+B2

1

0

1

0

B2P

0

1

1

0

B2P

B2P

B2P+B2

1

1

1

0

B2P+B2

B2P

Q2=P1X1X2Y1h+X2Y2+Y1Y2h+P1X1X2+P1X1X2+P1X1X2+X2h

Q1min = Y1Y2h + X1X2 + X1h + X1X2Y2h+X1Y2

Рmin = X1X2Y2h + X1Y1h

П=А2В1(В2+р)+А1В2(А2+р)+А1(А2р+В1)+В1В2р

S1=А1А2(В2р+В1р)+А1А2(В1+р)+В1В2р(А1+А2)+А1р(А2В1+А2В1)+А1В1В2

S2=А1А2В1(р+В2)+А1А2(В1р+В2р)+А2В2(В1р+В2р)+А1(А2В1р+В2р)

5.4. Логический синтез преобразователя множителя (ПМ)

Преобразователь множителя (ПМ) служит для исключения из множителя диад

Похожие материалы

Информация о работе

ВУЗ:
Белорусский государственный университет информатики и радиоэлектроники (БГУИР)
Предмет:
Арифметические и логические основы вычислительной техники
Тип:
Курсовые работы
Категория:
Информатика и выч. техника (Технические предметы)
Размер файла:
1 Mb
Скачали:
0
Скачать файл

Уважаемые коллеги! Предлагаем вам разработку программного обеспечения под ключ.

Опытные программисты сделают для вас мобильное приложение, нейронную сеть, систему искусственного интеллекта, SaaS-сервис, производственную систему, внедрят или разработают ERP/CRM, запустят стартап.

Сферы - промышленность, ритейл, производственные компании, стартапы, финансы и другие направления.

Языки программирования: Java, PHP, Ruby, C++, .NET, Python, Go, Kotlin, Swift, React Native, Flutter и многие другие.

Всегда на связи. Соблюдаем сроки. Предложим адекватную конкурентную цену.

Заходите к нам на сайт и пишите, с удовольствием вам во всем поможем.