















6 КОРРЕКЦИЯ ДИНАМИЧЕСКИХ СВОЙСТВ САУ
6.1 Способы включения корректирующих звеньев
Коррекция динамических
свойств САУ используется для выполнения требований по устойчивости, точности и
качеству процессов управления. Коррекция осуществляется с помощью введения в
систему специальных корректирующих звеньев с определенной, заранее подобранной
передаточной функцией ![]() . Корректирующие звенья
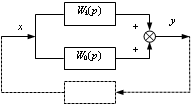
(КЗ) могут включаться последовательно (рис. 6.1, а) или параллельно
(рис. 6.1, б, в) с основными звеньями
. Корректирующие звенья
(КЗ) могут включаться последовательно (рис. 6.1, а) или параллельно
(рис. 6.1, б, в) с основными звеньями ![]() САУ,
поэтому они делятся на последовательные и параллельные КЗ. Из рис. 6.1, б,
в следует, что возможны два способа включения параллельных КЗ, но в дальнейшем
будем рассматривать только последний вариант включения КЗ, когда
САУ,
поэтому они делятся на последовательные и параллельные КЗ. Из рис. 6.1, б,
в следует, что возможны два способа включения параллельных КЗ, но в дальнейшем
будем рассматривать только последний вариант включения КЗ, когда ![]() .
.
 |
|||
а)
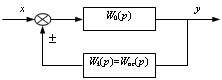
б)
в)
Рис. 6.1 - Включение корректирующих звеньев в САУ: последовательное (а), параллельное (б), обратная связь (в)
Последнее объясняется
тем, что в замкнутом контуре САУ КЗ, изображенное на рис. 6.1, б), тоже
может рассматриваться как обратная связь, но относительно другой части САУ,
показанной пунктиром. С другой стороны, схему на рис. 6.1, б) можно
свести и к последовательной коррекции (рис. 6.1, а), принимая за
передаточную функцию КЗ сумму ![]() . Рассмотрим
действие КЗ на конкретных примерах.
. Рассмотрим
действие КЗ на конкретных примерах.
6.2 Пропорционально-дифференцирующее
последовательное корректирующее звено
Изучение пропорционально-дифференцирующих (ПД) КЗ начнем с идеального пропорционально-дифференцирующего звена, имеющего передаточную функцию вида
![]() .
(6.1)
.
(6.1)
Из (6.1) видно, что
выходная величина ПД-звена содержит две составляющие: пропорциональную входной
величине, определяемую коэффициентом ![]() , и
пропорциональную ее первой производной, определяемой коэффициентом
, и
пропорциональную ее первой производной, определяемой коэффициентом ![]() . Вторая составляющая может быть
положительной или отрицательной.
. Вторая составляющая может быть
положительной или отрицательной.
Существуют также ПД-звенья, на выходе которых имеется составляющая, пропорциональная второй производной. Однако такую составляющую предпочитают получать последовательным включением двух звеньев с передаточной функцией (6.1).
Включение ПД-звена в
САУ приводит к тому, что передаточная функция ![]() разомкнутой
системы умножается на передаточную функцию этого КЗ, т.е. принимает вид
разомкнутой
системы умножается на передаточную функцию этого КЗ, т.е. принимает вид
![]() .
.
Следовательно, передаточная функция замкнутой САУ имеет следующий вид:
![]() .
.
В результате левая часть дифференциального уравнения замкнутой САУ становится такой, что характеристический многочлен можно записать в виде
![]() , где
, где ![]() .
.
Обычно ![]() , поэтому введение дополнительного
воздействия по производной с помощью ПД-звена позволяет изменить величину
коэффициента при
, поэтому введение дополнительного
воздействия по производной с помощью ПД-звена позволяет изменить величину
коэффициента при ![]() в 1-й степени в
многочлене
в 1-й степени в
многочлене ![]() . Применение ПД-звена со второй
производной или двух последовательных звеньев с передаточной функцией (6.1) приводит
к изменению коэффициента у
. Применение ПД-звена со второй
производной или двух последовательных звеньев с передаточной функцией (6.1) приводит
к изменению коэффициента у ![]() и т.д.
Изменение коэффициентов в многочлене
и т.д.
Изменение коэффициентов в многочлене ![]() изменяет
условия устойчивости и качество переходных процессов в САУ.
изменяет
условия устойчивости и качество переходных процессов в САУ.
Рассмотрим в качестве
примера использование ПД-звеньев для обеспечения устойчивости САУ с астатизмом
выше первого порядка. Пусть передаточная функция разомкнутой системы с порядком
астатизма, равным ![]() , имеет вид :
, имеет вид :
![]() , где
, где ![]() при
при ![]() .
.
Соответственно, характеристический многочлен для замкнутой системы
![]() .
(6.2)
.
(6.2)
Вспомним, что
необходимым условием устойчивости САУ является положительность коэффициентов
при ![]() всех степеней от 0 до
всех степеней от 0 до ![]() , где
, где ![]() -
порядок характеристического уравнения системы. Если
-
порядок характеристического уравнения системы. Если ![]() ,
то из (6.2) следует важный вывод о том, что САУ с порядком астатизма
,
то из (6.2) следует важный вывод о том, что САУ с порядком астатизма ![]() являются структурно неустойчивыми,
так как при этом в
являются структурно неустойчивыми,
так как при этом в ![]() отсутствуют члены с
отсутствуют члены с ![]() в степени от
в степени от ![]() до
до ![]() .
.
Введем в систему
ПД-звенья, дающие положительное воздействие по производным от первого до (![]() )-го порядков. При этом в
многочлене
)-го порядков. При этом в
многочлене ![]() появятся недостающие члены :
появятся недостающие члены :
![]() . (6.3)
. (6.3)
Из (6.3) следует, что при введении в систему ПД-звеньев, дающих положительное воздействие по производным, САУ становится структурно устойчивой.
Аналогично
доказывается, что с помощью дополнительного воздействия по производным можно
сделать устойчивой систему, структурно неустойчивую из-за наличия в ней
неустойчивых звеньев, создающих в ![]() члены с
отрицательными коэффициентами. Применение дополнительного воздействия позволяет
изменить в
члены с
отрицательными коэффициентами. Применение дополнительного воздействия позволяет
изменить в ![]() знак этих коэффициентов.
знак этих коэффициентов.
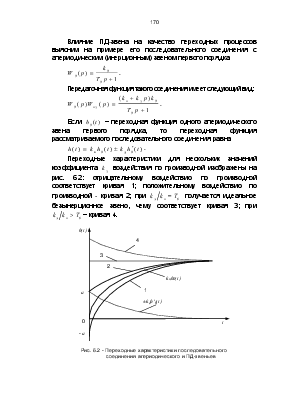
Влияние ПД-звена на качество переходных процессов выясним на примере его последовательного соединения с апериодическим (инерционным) звеном первого порядка
![]() .
.
Передаточная функция такого соединения имеет следующий вид:
![]() .
.
Если ![]() - переходная функция
одного апериодического звена первого порядка, то переходная функция
рассматриваемого последовательного соединения равна
- переходная функция
одного апериодического звена первого порядка, то переходная функция
рассматриваемого последовательного соединения равна
![]() .
.
Переходные характеристики для нескольких значений коэффициента
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.