Алгоритм решения транспортной задачи с нарушенным балансом

1.2 АЛГОРИТМ РЕШЕНИЯ

1.2.1 Общие понятия и определения

Транспортам задача относится к классу задач линейного программирования. Транспортная задача решает проблему нахождения оптимального (минимального по стоимости) плана распределения и перемещения ресурсов от производителей к потребителям. Проблема оптимизации стоимости перевозок актуальна и на сегодняшний день, так как позволяет фирмам и предприятиям существенно сократить расходы на транспорт. Правильная организация перевозок позволяет устранить встречные и дублирующие перевозки, сократить количество дальних перевозок и т.д. При решении транспортной задачи необходимо:

- обеспечить всех потребителей ресурсами;

- распределить все произведенные ресурсы;

- переместить ресурсы от производителей к потребителям с оптимальными затратами.

От каждого производителя ресурс может перемещаться к любому потребителю и измеряться в одних единицах измерения.

1.2.2 Математическая формулировка транспортной задачи

От каждого i-го производителя произведенный им ресурс а может перемещаться j-му потребителю ресурса в объеме, не превышающем b. Таким образом, x будет означать перемещение некоторого числа единиц ресурса от i-го производителя к j-му потребителю. Через c обозначим стоимость перемещения единицы ресурса от i-го производителя к j-му потребителю.

Тогда матрица X={x} будет называться матрицей перевозок или планом перевозок и, соответственно, матрица C={c} матрицей стоимости.

Предполагаем, что суммарный объем произведенного ресурса в точности совпадает с объемом потребления ресурса (задача закрытого типа). Понятно, что любой план перевозок X, обеспечивающий распределение ресурса между потребителями, будет допустимым. Суммарная стоимость всех перевозок, вычисленная по любому допустимому плану, будет

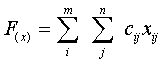                                                              (1)

Оптимальным планом перевозок X будет называться тот из допустимых планов перевозок, который обеспечит минимальную сумму затрат на перевозку всех ресурсов.

Отсюда следует, что исходные данные транспортной задачи задаются вектором произведенных ресурсов А={a}, вектором потребления ресурсов B={b} и матрицей стоимостей C={c} при i=1,…,m и j=1,…,n, где m - общее число производителей ресурса, а n – общее число потребителей ресурса.

Математическая модель транспортной задачи:

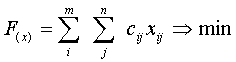                                               (2)

При ограничениях:

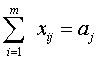                                                                           (3)

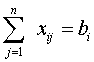                                                                           (4)

где ; ; .

Таким обрезом, транспортную задачу можно решить симплексным методом, но при этом потребуется выполнить большое количество расчетов матрицы.

По аналогии с симплексным методом допустимым решением будем называть любое решение, которое удовлетворяет условиям (3) и (4). Опорным решением будем называть такое, которое имеет m+n-1 перевозок, отличных от нуля. Оптимальным решение будет одно из опорных решений, которое обеспечивает минимальную сумму затрат по всем перевозкам.

Если при решении задачи линейного программирования симплексным методом требовалось на каждом шаге пересчитать матрицу целиком, то при решении транспортной задачи одним из методов поиска оптимального решения пересчитывается только часть матрицы (замкнутый контур), что резко сокращает количество вычислений.

1.2.3. Построение опорного плана перевозок

Для того чтобы начать решение транспортной задачи, надо построить опорный план. Опорный (или начальный) план является одним из допустимых планов.

1.2.4. Метод «северо-западного угла»

При использовании этого метода опорный план перевозок начинают строить с левого верхнего (северо-западного) угла матрицы перевозок по  следующему алгоритму:

1.  Первому потребителю назначается ресурс от первого производителя. При этом возможны следующие варианты:

- запрос первого потребителя удовлетворён не полностью, тогда недостающий ресурс первому потребителю добавляют от второго производителя и при необходимости от третьего производителя, до тех пор пока потребности первого потребителя не будут полностью обеспечены;

- запрос первого потребителя удовлетворён полностью. Остаток ресурса от первого производителя назначают второму потребителю, а при необходимости и третьему потребителю и т.д.;

- запрос первого потребителя обеспечен полностью ресурсом первого производителя, и ресурс первого производителя израсходован полностью. Далее переходят к обеспечению запроса второго потребителя.

2. Затем обеспечивают потребности второго потребителя по образцу первого потребителя. И так далее пока не будут обеспечены запросы всех потребителей.

1.2.5. Метод минимальных элементов

Суть метода состоит в том, что в матрице стоимостей C={c} выбирается стоимость минимальной перевозки c. Затем назначается максимальный объём ресурса от производителя i к потребителю j для данной перевозки. При этом возможны три варианта:

1) производитель i имеет ресурса больше, чем надо потребителю j.