Решение задачи конвективного теплообмена на поверхности внутреннего цилиндра методом гидродинамической теории теплообмена

4.4. Решение задачи конвективного теплообмена на поверхности внутреннего цилиндра методом гидродинамической теории теплообмена

Процесс теплообмена при движении теплоносителя у поверхности стенки непрерывно связан с переносом количества движения. Поэтому для расчета теплоотдачи в турбулентных пристенных слоях широко применяется гидродинамическая аналогия Рейнольдса [l61,169,131,144].

Используем методику расчета теплообмена по данной схеме для цилиндра, находящегося в циклонной камере кольцевого сечения. Предварительно сделаем некоторые замечания относительно напряжения трения и коэффициента сопротивления.

Ранее уже отмечалось (гл.3.3), при  напряжение поверхностного трения в пределах ядра потока, практически, не меняется по длине цилиндра. При  оно существенно переменно, но, однако, общий характер его изменения в условиях опыта оказался таким, что среднеинтегральное значение по длине вставки близко к его величине в среднем сечении (). Поэтому приводимые опытные данные и полученные на их базе решения для сечения  могут рассматриваться не только как имеющие локальное значение, но и как среднеинтегральные в пределах ядра потока.

С целью сопоставления уравнения (4.86) с найденной далее на основе аналогии Рейнольдса зависимостью а также проверки универсальности свойств комплекса D_w, в работе сделана попытка обобщить с помощью этого критерия опытные данные по трению, универсальному распределению скоростей и т.д. Принятое решение обосновывается тем, что основную роль в формировании пограничного слоя, как было показано ранее, играют центробежные силы. В этом случае, значения коэффициентов в уравнениях (3.19) … (3.20)и безразмерные толщины пограничного слоя для ядра потока выражаются следующими зависимостями:

                                                (4.89)

                                                (4.90)

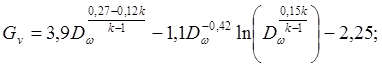                            (4.91)

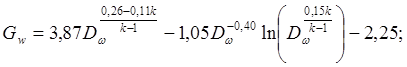                        (4.92)

                                                (4.93)

                                               (4.94)

где     k=1/n – обратная величина показателя зависимости (3.1)(n=n_v) или (3.2) (n=n_j).

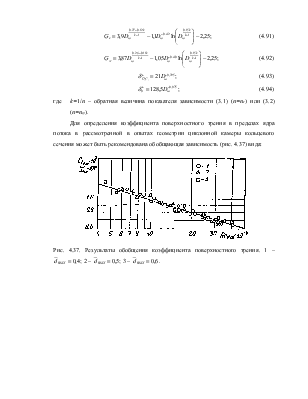
Для определения коэффициента поверхностного трения в пределах ядра потока в рассмотренной в опытах геометрии циклонной камеры кольцевого сечения может быть рекомендована обобщающая зависимость (рис. 4.37) вида:

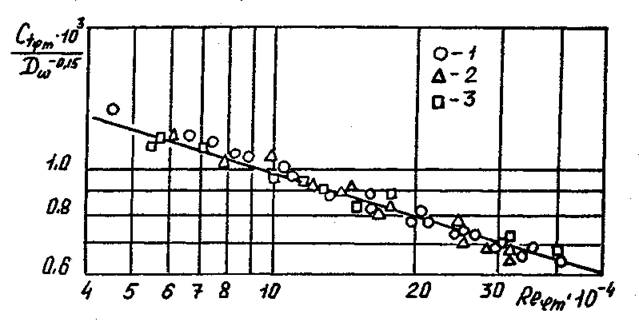
Рис. 4.37. Результаты обобщения коэффициента поверхностного трения. 1 – ; 2 – ; 3 – .

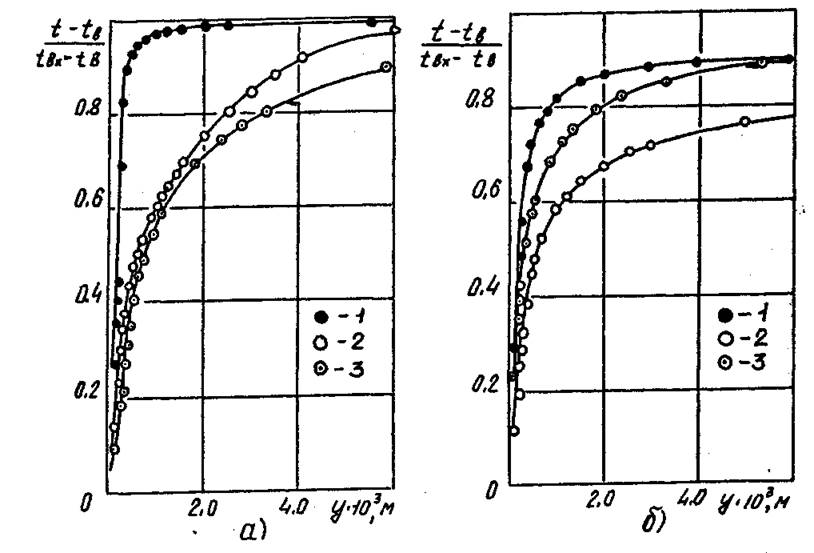
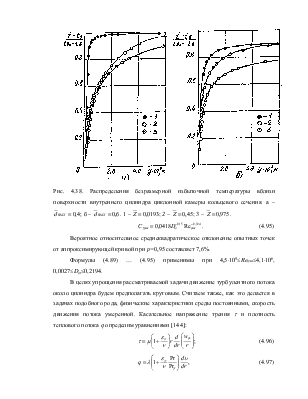
Рис. 4.38. Распределения безразмерной избыточной температуры вблизи поверхности внутреннего цилиндра циклонной камеры кольцевого сечения. а – ; б – . 1 – ; 2 – ; 3 – .

                                 (4.95)

Вероятное относительное среднеквадратическое отклонение опытных точек от аппроксимирующей кривой при р=0,95 составляет 7,6%.

Формулы (4.89) … (4.95)применимы при 4,5×10⁵£Re_jm£4,1×10⁶, 0,0027£D_w£0,2194.

В целях упрощения рассматриваемой задачи движение турбулентного потока около цилиндра будем предполагать круговым. Считаем также, как это делается в задачах подобного рода, физические характеристики среды постоянными, скорость движения потока умеренной. Касательное напряжение трения tи плотность теплового потока q определим уравнениями [144]:

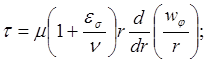                                     (4.96)

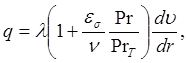                                         (4.97)

где     e_s – кинематический коэффициент турбулентного переноса количества движения; Pr_Т– турбулентное число Прандтля; u=t-t_В– избыточная температура среды.

Используя условия сохранения (в радиальном направлении) момента сил трения:

                                  (4.98)

и конвективного теплового потока:

                                      (4.99)

где     q_B – плотность теплового потока на поверхности цилиндра, и введя универсальные переменные ; ;  ( – динамическая скорость, y – расстояние по нормали; ) преобразуем уравнения (4.96) … (4.99).

Из выражений (4.96) и (4.98) следует:

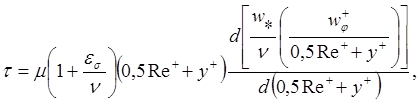                    (4.100)

где      – число Рейнольдса, построенное по динамической скорости, и

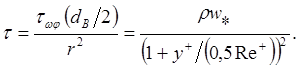                              (4.101)

Из выражений (4.97) и (4.99) также следует

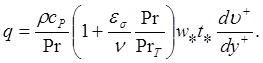                          (4.102)

и

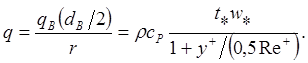                        (4.103)

Приравнивая отношение выражений (4.100) к (4.101) и (4.102) к (4.103) между собой получим:

.

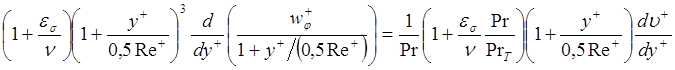Тогда уравнение, связывающее распределение скорости и температуры в универсальных переменных будет иметь вид:

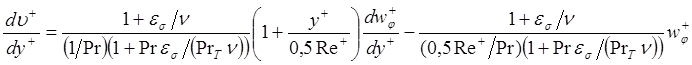.  (4.104)

В работе [199] выражение 1/(0,5Re⁺) определялось как параметр для учета влияния кривизны на течение у стенки криволинейного канала )в опытах диапазон изменения Re⁺ составлял:  – Re⁺=900...5000;  – Re⁺=1700...4200;  – Re⁺ =1100...2300).

Для решения уравнения (4.104) в целях упрощения полагаем, что в ламинарном подслое , а в турбулентном ядре . В переходной (буферной) области в соответствии с уравнениями (4.100) и (4.101) соотношение  находится из следующего выражения: