Решение задачи конвективного теплообмена на поверхности внутреннего цилиндра методом гидродинамической теории теплообмена, страница 5

На рис.4.41 представлено сопоставление опытных данных со степенной аппроксимацией температуры (4.115) для двух предельных случаев движения потока ( и ) в сечении с . Некоторое отличие в показателях n_v (зависимость 3.1) и m для случая, когда максимум w_j «прижат» к поверхности цилиндра так же, вероятно, можно объяснить существованием осевого конвективного переноса теплоты.

Формулы (4.108) … (4.114) позволяют найти температурные напоры в пристенном пограничном слое. Для определения температурного напора в струйном пограничном слое () можно воспользоваться следующими эмпирическими уравнениями:

для потока с «прижатым» максимумом    w_j (200£y⁺£600)

,                                  (4.116)

для потока с «прижатым» максимумом    w_j (150£y⁺£1200)

,                                   (4.117)

где      – безразмерная температура на границе турбулентного ядра динамического пограничного слоя.

В работе была опробована и обработка температуры в струйном пограничном слое в виде функции:

, где     , t₀ – температура на границе струйного пограничного слоя (на радиусе r_jm).

Оказалось, что такое распределение температуры в струйной части пограничного слоя удовлетворительно аппроксимируется зависимостью, применявшейся для описания безразмерного тангенциального профиля (1.8):

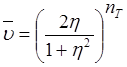.                                               (4.118)

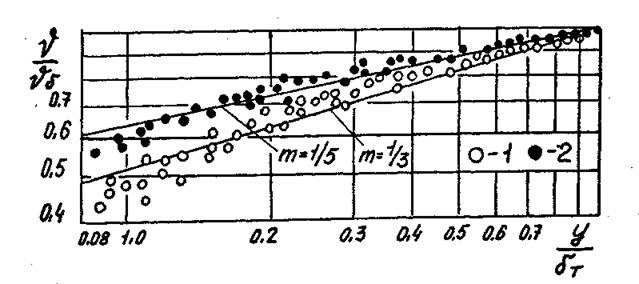
Рис. 4.41. Распределения температуры в пристенном пограничном слое. 1 – ; 2 – .

Рис. 4.42. Распределение температуры в струйном пограничном слое. 1 – ; 2 – .

Однако показатель степени n_Т для температуры должен браться вдвое меньшим, чем для скорости (рис.4.42).

При известном общем температурном напоре u⁺ плотности теплового потока на поверхности цилиндра можно рассчитать коэффициент теплоотдачи a и получить расчетное уравнение подобия:

,                                                 (4.119)

где      – число Нуссельта,  – число Рейнольдса;  .

В этом случае для циклонного потока с «прижатым» к цилиндру максимумом w_j уравнение имеет вид:

,                                             (4.120)

Для потока со «свободным» максимумом w_j:

,                                             (4.121)

Результаты сопоставления опытных и расчетных данных по теплоотдаче (при Pr=0,71) в пределах ядра потока приведены на рис.4.43.

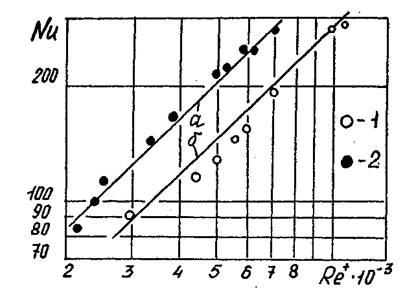
Рис. 4.43. Сопоставление опытных и расчетных данных по теплоотдаче внутреннего цилиндра. Расчет: a – по уравнению (4.120); б – по уравнению (4.121). 1 – ; 2 – .

Для первого рассматриваемого варианта положения w_j лучшая сходимость расчетных и опытных данных достигается при Рr_T=0,9, а во втором при Рr_T=0,75, что вполне соответствует ранее рассмотренным физическим представлениям об изменении уровня турбулентности потока по радиусу камеры. Уравнением (4.121) (для камеры с ) обеспечивается наиболее полное соответствие опытным данным, чем уравнением (4.120) для камеры с . Данное обстоятельство, вероятно, можно объяснить теми же причинами, что и расхождение опытных и расчетных профилей u⁺. Более высокий уровень теплоотдачи во втором случае (4.121) по сравнению с первым (4.120) может быть объяснен и менее значительным консервативным влиянием центробежных сил на процессы переноса в турбулентном ядре пристенного пограничного слоя. Подтверждением последнего является и то, что уравнение (4.121) близко к полученным аналогичным зависимостям для расчета теплоотдачи в других задачах [25,26].

Уравнениям (4.120) и (4.121) можно придать и другой вид, если определить входящее в них напряжение трения по ранее рассмотренным формулам для коэффициента поверхностного трения. С этой целые используем обобщающие эмпирические зависимости:

,                                          (4.122)

и

.                                           (4.123)

В результате выполнения преобразований с учетом изменения плотности по длине вставки получим

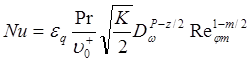.                                    (4.123)

где     K; z; P; m; e_q (соотношение между интегральной плотностью теплового потока по длине цилиндра и его частью в пределах ядра потока) – опытные коэффициенты.