1.Побудувати модель парної лінійної регресії.
|
Варіант № 8 |
||
|
№ |
||
|
1 |
2,7 |
14,9 |
|
2 |
2,5 |
16,1 |
|
3 |
2,1 |
19,7 |
|
4 |
2,8 |
14,0 |
|
5 |
2,4 |
17,1 |
|
6 |
2,3 |
18,2 |
|
7 |
2,5 |
17,4 |
|
8 |
2,7 |
16,1 |
|
9 |
2,4 |
18,0 |
Заповнимо наступну таблицю в Excel.
|
№ |
Xi |
Yi |
Xi*Yi |
Xi2 |
Yi2 |
|
|
|
1 |
2,7 |
14,9 |
40,23 |
7,29 |
222,01 |
15,2337 |
0,3337 |
|
2 |
2,5 |
16,1 |
40,25 |
6,25 |
259,21 |
16,7491 |
0,6491 |
|
3 |
2,1 |
19,7 |
41,37 |
4,41 |
388,09 |
19,7800 |
0,0800 |
|
4 |
2,8 |
14,0 |
39,20 |
7,84 |
196 |
14,4760 |
0,4760 |
|
5 |
2,4 |
17,1 |
41,04 |
5,76 |
292,41 |
17,5069 |
0,4069 |
|
6 |
2,3 |
18,2 |
41,86 |
5,29 |
331,24 |
18,2646 |
0,0646 |
|
7 |
2,5 |
17,4 |
43,50 |
6,25 |
302,76 |
16,7491 |
-0,6509 |
|
8 |
2,7 |
16,1 |
43,47 |
7,29 |
259,21 |
15,2337 |
-0,8663 |
|
9 |
2,4 |
18,0 |
43,20 |
5,76 |
324 |
17,5069 |
-0,4931 |
|
Сума |
22,4 |
151,5 |
374,1 |
56,1 |
2574,9 |
151,5000 |
0,0000 |
![]() Модель парної лінійної
регресії будуємо за формулою:
Модель парної лінійної
регресії будуємо за формулою:
Знаходимо середні значення X та Y:
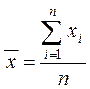
![]() =
2,4889
=
2,4889
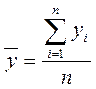
![]() = 16,8333.
= 16,8333.
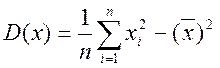 Далі знаходимо cov(x,y)= -0,3274 та D(x)= 0,0432
за формулами:
Далі знаходимо cov(x,y)= -0,3274 та D(x)= 0,0432
за формулами:
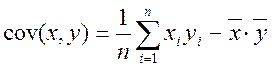 |
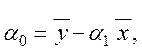
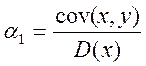 Обчислимо
коефіцієнти
Обчислимо
коефіцієнти ![]() та
та ![]() :
:
![]() =-7,5771
=-7,5771
![]() =35,6920.
=35,6920.
Модель парної лінійної регресії набуває вигляду: Y=35,6920-7,5771X.
Розраховуємо модельні значення ![]() та заносимо їх до
таблиці.
та заносимо їх до
таблиці.
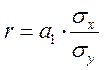 Оцінимо якість
створеної моделі.
Оцінимо якість
створеної моделі.
Знаходимо коефіцієнт кореляції r: , де
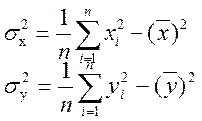 |
![]() =0,0432
=0,0432
![]() =2,7422
=2,7422
r=-0,9511
Коефіцієнт кореляції показує, як в середньому змінюється результативна ознака (У), якщо фактор (Х) збільшиться на 1, тому:
![]() , коли х
зростає, у спадає.
, коли х
зростає, у спадає.
Знаходимо
коефіцієнт детермінації (![]() ). Коефіцієнт детермінації використовується
як критерій адекватності моделі, бо є мірою пояснювальної сили незалежної
змінної х.
). Коефіцієнт детермінації використовується
як критерій адекватності моделі, бо є мірою пояснювальної сили незалежної
змінної х.
![]()
![]() =0,9047.
=0,9047.
2.Перевірити на наявність мультиколінеарності незалежні змінні, та усунути мультиколінеарність, якщо вона є.
|
№8 |
|||
|
у |
х1 |
х2 |
х3 |
|
1,00 |
5,60 |
3,00 |
2,80 |
|
0,50 |
1,80 |
4,00 |
0,90 |
|
0,60 |
5,80 |
5,00 |
2,90 |
|
0,20 |
3,20 |
6,00 |
1,60 |
|
0,30 |
6,00 |
3,00 |
3,00 |
|
0,40 |
5,00 |
6,80 |
2,50 |
|
0,80 |
9,80 |
3,01 |
4,90 |
|
0,60 |
2,00 |
0,61 |
1,00 |
|
0,40 |
4,80 |
1,40 |
2,40 |
|
0,30 |
3,50 |
1,70 |
1,10 |
1. Кількість спостережень n=10, кількість факторів m=3. Визначимо, чи присутня мульиколінеарність за допомогою алгоритма Фаррара-Глобера
В Excel заповнюємо наступну таблицю та проводимо розрахунки середніх значень кожної змінної та дисперсії за допомогою формул:
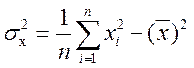
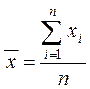
|
№ |
у |
х1 |
х2 |
х3 |
X1i2 |
X2i2 |
X3i2 |
|
1 |
1,00 |
5,60 |
3,00 |
2,80 |
31,36 |
9,00 |
7,84 |
|
2 |
0,50 |
1,80 |
4,00 |
0,90 |
3,24 |
16,00 |
0,81 |
|
3 |
0,60 |
5,80 |
5,00 |
2,90 |
33,64 |
25,00 |
8,41 |
|
4 |
0,20 |
3,20 |
6,00 |
1,60 |
10,24 |
36,00 |
2,56 |
|
5 |
0,30 |
6,00 |
3,00 |
3,00 |
36,00 |
9,00 |
9,00 |
|
6 |
0,40 |
5,00 |
6,80 |
2,50 |
25,00 |
46,24 |
6,25 |
|
7 |
0,80 |
9,80 |
3,01 |
4,90 |
96,04 |
9,06 |
24,01 |
|
8 |
0,60 |
2,00 |
0,61 |
1,00 |
4,00 |
0,37 |
1,00 |
|
9 |
0,40 |
4,80 |
1,40 |
2,40 |
23,04 |
1,96 |
5,76 |
|
10 |
0,30 |
3,50 |
1,70 |
1,10 |
12,25 |
2,89 |
1,21 |
|
Сума |
5,10 |
47,50 |
34,52 |
23,10 |
274,81 |
155,52 |
66,85 |
|
|
4,7500 |
σ2x1 = |
4,9185 |
||
|
|
3,4520 |
σ2x2 = |
3,6359 |
||
|
|
2,3100 |
σ2x3 = |
1,3489 |
Знайдемо матрицю X, що складається із нормалізованих змінних. Розрахунки
проводимо за формулою: 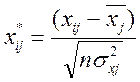
|
0,1212 |
-0,0750 |
0,1334 |
|
-0,4206 |
0,0909 |
-0,3839 |
|
0,1497 |
0,2567 |
0,1606 |
|
-0,2210 |
0,4226 |
-0,1933 |
|
0,1782 |
-0,0750 |
0,1879 |
|
0,0356 |
0,5552 |
0,0517 |
|
0,7201 |
-0,0733 |
0,7052 |
|
-0,3921 |
-0,4713 |
-0,3567 |
|
0,0071 |
-0,3403 |
0,0245 |
|
-0,1782 |
-0,2906 |
-0,3295 |
Обчислюємо
кореляційну матрицю ![]() та обчислимо її
визначник.
та обчислимо її
визначник.
|
1,0000 |
0,0856 |
0,9863 |
|
0,0856 |
1,0000 |
0,1331 |
|
0,9863 |
0,1331 |
1,0000 |
detR=0,0246.
Обчислимо критерій ![]() за формулою
за формулою 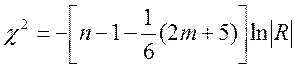 :
:
![]() =29,6331
=29,6331
Порівняємо знайдене
значення з табличним при ![]() =0,05, ступені свободи 3.
=0,05, ступені свободи 3.
![]() =7,8.
=7,8.
Якщо ![]() , то в даній моделі спостерігається
явище мультиколінеарності.
, то в даній моделі спостерігається
явище мультиколінеарності.
2. Знаходимо
матрицю похибок за формулою: ![]()
|
39,8952 |
1,8573 |
-39,5962 |
|
1,8573 |
1,1045 |
-1,9789 |
|
-39,5962 |
-1,9789 |
40,3175 |
Розраховуємо F-критерії за
формулою: 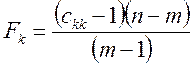 , де
, де ![]() - діагональні елементи.
- діагональні елементи.
F1=136,13
F2=0,37
F3=137,61.
Порівнюємо з табличним значенням:
![]() =
19,36.
=
19,36.
Значення F- критеріїв для першого та третього факторів більші за табличні, це означає, що змінні X1 та X3 мультиколінеарні з іншими.
Обчислимо
коефіцієнти детермінації для кожної змінної за формулою: 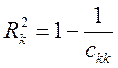
R12=0,97
R22=0,09
R32=0,98.
3. Знайдемо критерій Стьюдента.
Для цього спочатку обчислимо
часткові коефіцієнти кореляції за формулою: 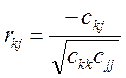
r12=-0,28
r13=0,99
r23=0,3.
Коефіцієнти кореляції характеризують щільність зв’язку між двома змінними за умови, що інші змінні не впливають на цей зв'язок. Можемо зробити висновок тільки про щільний зв’язок між змінними X1 та X3.
Розрахуємо t-
критерій за формулою:
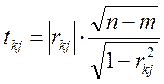 :
:
t12=0,77
t13=16,44
t23=0,82.
Порівнюємо з
табличними при значущості 0,05 та ступені свободи 7 (![]() =2,36).
Оскільки лише
=2,36).
Оскільки лише ![]() , то між першою та третьої
змінними існує мультиколінеарність. Для усунення мультиколініарності вилучимо з
моделі одну із цих змінних. Зупинимося на X3, що має більший F-критерії.
, то між першою та третьої
змінними існує мультиколінеарність. Для усунення мультиколініарності вилучимо з
моделі одну із цих змінних. Зупинимося на X3, що має більший F-критерії.
Побудувати
квазілінійні парні регресії та визначити їх адекватність.
|
№8 |
|
|
Х |
У |
|
0 |
11,1 |
|
1 |
12,5 |
|
2 |
19,8 |
|
3 |
12,4 |
|
4 |
11,1 |
Заповнюємо таблицю в Excel:
|
№ |
Xi |
Yi |
Xi^0,5 |
Xi^0,5*Yi |
Xi^2 |
Xi^2*Yi |
exp(Xi) |
exp(Xi)*Yi |
Xi4 |
exp(2Xi) |
|
1 |
0 |
11,1 |
0,00 |
0,00 |
0,00 |
0,00 |
1,00 |
11,10 |
0,00 |
1,00 |
|
2 |
1 |
12,5 |
1,00 |
12,50 |
1,00 |
12,50 |
2,72 |
33,98 |
1,00 |
7,39 |
|
3 |
2 |
19,8 |
1,41 |
28,00 |
4,00 |
79,20 |
7,39 |
146,30 |
16,00 |
54,60 |
|
4 |
3 |
12,4 |
1,73 |
21,48 |
9,00 |
111,60 |
20,09 |
249,06 |
81,00 |
403,43 |
|
5 |
4 |
11,1 |
2,00 |
22,20 |
16,00 |
177,60 |
54,60 |
606,04 |
256,00 |
2980,96 |
|
Сума |
10,00 |
66,90 |
6,15 |
84,18 |
30,00 |
380,90 |
85,79 |
1046,48 |
354,00 |
3447,37 |
Складемо регресійні моделі, в яких робиться заміна лише показника.
1) ![]()
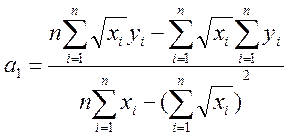 = 0,79
= 0,79
![]() =12,4
=12,4
![]()
2) ![]()
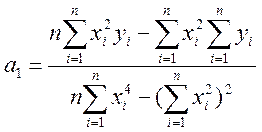 = -0,12
= -0,12
![]() =14,09
=14,09
![]()
3) ![]()
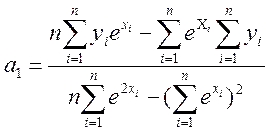 = -0,05
= -0,05
![]() =14,26
=14,26
![]()
Розрахуємо значення критерія Фішера за формулами:
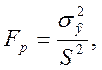 де
де 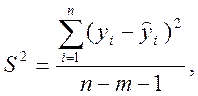

де n=5- число дослідів, m=1-число включених у регресію факторів, які чинять суттєвий вплив на показник.
Порівняємо розрахункове значення критерія Фішера з табличним для α=0,01, k1=m=1, k2=n-m=5-1=4.
F=21,2. Якщо ![]() то з надійністю
то з надійністю ![]() можна вважати, що
розглянута математична модель адекватна експериментальним даним, у протилежному
випадку з надійністю Р розглянуту парну регресію не можна вважати адекватною.
можна вважати, що
розглянута математична модель адекватна експериментальним даним, у протилежному
випадку з надійністю Р розглянуту парну регресію не можна вважати адекватною.
Проводимо розрахунки, заповнюючи в Excel відповідні таблиці.
1. ![]()
|
S2= |
17,27 |
|
σ2y = |
1,54 |
|
Fp= |
0,09 |
Модель неадекватна.
2. ![]()
|
S2= |
16,98 |
|
σ2y = |
2,42 |
|
Fp= |
0,14 |
Модель неадекватна.
3. ![]()
|
S2= |
16,05 |
|
σ2y = |
5,21 |
|
Fp= |
0,32 |
Модель неадекватна.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.