Расчет привода конвейера (окружное усилие на барабане - 13 кН, окружная скорость - 0,6 м/с), страница 4

d_ae1 = d_e1 + 2 ∙ m_e ∙ cosδ₁ = 114,6 + 2 ∙ 3,37 ∙ cos 11º31′ = 121,2 мм колеса

d_ae2 = d_e2 + 2 ∙ m_e ∙ cosδ₂ = 560 + 2 ∙ 3,37 ∙ cos 78º29′ = 561,4 мм

4.11 Внешний диаметр окружности впадин зубьев шестерни

d_fe1 = d_e1 – 2,4 ∙ m_e ∙ cosδ₁ = 114,6 – 2,4 ∙ 3,37 ∙ cos 11º31′ = 106,7 мм колеса

d_fe2 = d_e2 – 2,4 ∙ m_e ∙ cosδ₂ = 560 – 2,4 ∙ 3,37 ∙ сos 78º29′ = 558,6 мм

4.12 Окружная скорость зубчатых колёс

υ = ω₁ ∙ = 3,78 м/с

Определяем степень точности по таблице 1.4 [3]. Принимаю степень точности 8

4.13 Угол ножки зуба

 = 1º21′

4.14 Угол головки зуба

= 1º08′

4.15 Углы конусов вершин зубьев шестерни

δ_а1 = δ₁ + θ_а = 11º31′ + 1º21′ = 12º52′

колеса

δ_а2 = δ₂ + θ_а =  78º29′ + 1º21′ = 79º50′

4.16 Окружная сила на шестерне и колесе

F_t1 = F_t2 =  = 11737 Н

4.17 Осевая сила на шестерне, радиальная сила на колесе

F_a1 = F_r2 = F_t ∙ tg α_w ∙ sinδ₁ = 11737 ∙ tg 20º ∙ sin 11º31′ = 818,8 Н

где  α_w - угол зацепления = 20º

4.18 Радиальная сила на шестерне, осевая сила на колесе, Н

F_r1 = F_a2 = F_t ∙ tg α_w ∙ cos δ₁ = 11737 ∙ tg 20º ∙ cos 11º31′ = 4188,9 Н

4.19 Расчётное контактное напряжение

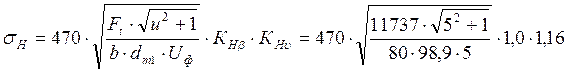= 623 МПа где         К_Нβ – коэффициент неравномерности нагрузки по длине зуба для                        прирабатывающихся зубьев К_Нβ = 1,0

К_Нυ – коэффициент динамической нагрузки определяется по таблице 1.5 [3] в зависимости от окружной скорости и степени точности передачи К_Нν = 1,16

Допускается 15% недогрузки по сравнению с допускаемым напряжением [σ_H].

∆ = 2,8%

2,8% < 15%   условие выполняется

4.20 Расчёт напряжения изгиба для шестерни

  

для колеса

  

где          Y_F – определяется по таблице 1.6 [3] для шестерни и колеса по эквивалентному числу их зубьев

z_v1 = z₁/cos δ1    z_v2 = z₂/cos δ2

z_v1 = 34/cos 11º31′ = 34,7

z_v2 = 166/cos 78º29′ = 817,9

Принимаю Y_F1 = 3,75, Y_F2 = 3,61, K_Fβ = 1,0, К_Fυ определяется по таблице 1.5 [3] в зависимости от окружной скорости и степени точности передачи К_Fυ = 1,38, К_Fα = 1,0

 = 265,1 МПа

= 255,2 МПа

σ_F1 ≤ [σ_F1]_ф            265,1 ≤ 583

условие выполняется

σ_F2 ≤ [σ_F2]_ф                   255,2 ≤ 467

условие выполняется большая разница объясняется тем, что напряжения изгиба в закрытой конической передаче незначительны

4.21 Конструирование конических зубчатых колёс

4.21.1 Конструирование обода

Внешние углы зубьев притупляются фаской: 

f ≈ 0,5 ∙ m_e = 0,5 ∙ 3,37 = 1,69 мм толщина S определяется по формуле:

S = 2,5 ∙ m_e + 2 мм = 2,5 ∙ 3,37 +2 = 10,4 мм ширина базового торца зубчатого венца

b_т = ( 1,0…1,1) ∙ S = 1 ∙ 10,4 = 11,4 мм ширина зубчатого венца b = 80 мм

4.21.2 Конструирование диска

Толщина диска “C” для конструкции зубчатых колёс принимается из соотношения С ≥ 0,25 ∙ b

C = 20 мм

4.21.3 Конструирование ступицы

Внутренний диаметр ступицы равен соответствующему диаметру вала d_в, который ориентировочно определяется по формуле

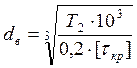
где          Т₂ – предаваемый валом вращающий момент, Н∙м

[τ_кр] – 20…30 МПа – допускаемое напряжение кручения

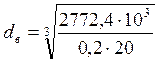= 88,5 мм

Округляю внутренний диаметр ступицы по Ra40 d_в = 90 мм (ГОСТ 6636-69, СТ СЭВ 208-75)

Наружный диаметр ступицы d_ст = 1,55 ∙ 90 = 139,5 мм по Ra40 d_cт = 140 мм

Длина ступицы l_cт = (1,2…1,5) ∙ d_в = 108 мм

Размеры шпоночного паза в ступице – ширина b и глубина t₂ определяются по таблице 1.10 [4] (ГОСТ 23360-78)

b = 25 мм;   h = 14 мм;  t₂ = 5,4 мм

4.22 Выбор конического одноступенчатого редуктора

Выбор редуктора производится по передаточному числу U_ред = 5 и номинальному крутящему моменту на тихоходном валу (Т₃ = 2772,4 Н∙м). Исходя из этого выбираю [5] редуктор  с типоразмером К - 315

Основные параметры:

Номинальное передаточное число - 5

Номинальная радиальная нагрузка на выходном валу, быстроходном - 3550 Н          тихоходном – 5600 Н

КПД – 0,98

масса – 180 кг

Габаритные и присоединительные размеры, мм