Построение графика зависимости общей стоимости запасов от максимального числа пополнений в единицу времени

СОДЕРЖАНИЕ

1.  Формулировка задачи………………..……………………………3

2.  Построение модели………………………………………………..5

3.  Разработка алгоритма………………………………………..……6

Заключение……………………………………………………………….7

Список используемой литературы……………………………………..8

Приложения……………………………………………………………...9

Приложение 1 SQL – запрос на создание таблицы Wodka …………..10

Приложение 2 Один из SQL – запроса на создание таблицы определенного вида водки …………………………………………………....11

Приложение 3 Расчёты по исходным данным ……….……………….12

Приложение 4 График зависимости C(N) …………………………….13

1. ФОРМУЛИРОВКА ЗАДАЧИ

В программе расчёта оптимальных размеров партий по минимуму стоимости запасов при ограничении на общее число пополнений в единицу времени, требуется построить график зависимости общей стоимости запасов (С) от максимального числа пополнений в единицу времени (N).

Для того чтобы рассчитать зависимость С(N) нужно:

1.  рассчитать множитель Лагранжа (μ);

2.  оптимальные размеры партий q_i.

Вычисление множителя Лагранжа производится по формуле:

μ = 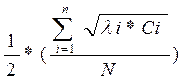²;

Оптимальные размеры партий вычисляются следующим образом:

q_i =, где n – число наименований продуктов,

N – максимальное число пополнений в единицу времени,

q_i – оптимальные размеры партий, i = 1, 2, …n,

λ_i = спрос в единицу времени на i – й продукт,

C_i = стоимость единицы i – го продукта

Общую стоимость запасов вычисляем по формуле:

С =

Решение данной задачи определяется построением графика С(N) в результате которого можно наглядно увидеть зависимость. Исходными данными являются значения λ_i и С_i, см. «табл. 1», которые взяты из базы данных, путём отбора.

Таблица 1. Значения спроса в единицу времени на i – продукт и стоимость единицы i – го продукта

2. ПОСТРОЕНИЕ МОДЕЛИ

Решение поставленной задачи можно разделить на три отдельных этапа. Первый этап определяет значение множителя Лагранжа (μ) при заданных значениях λ_i и С_i.

На втором этапе производится расчёт оптимальных размеров партий q_i на основании полученных значений λ_i и С_i.

В третьем этапе, получив значения оптимальных объёмов партий нужно вычислить общую стоимость запасов С.

После расчёта значения С необходимо построить график зависимости С(N). С учётом поставленной задачи нужно отобрать данные из базы данных с помощью SQl-запросов. Первый запрос отбирает данные и продукте «водка» и создает соответствующую таблицу см. Приложение 1. Остальные запросы осуществляют выборку по видам водки.

3. РАЗРАБОТКА АЛГОРИТМА

Для осуществления поставленной задачи с использованием выше предложенной модели будем:

1.  осуществлять выборку данных;

2.  осуществлять расчет по соответствующим формулам;

3.  осуществлять графический вывод зависимости C(N);

Для реализации первого пункта будем использовать SQL-запросы см. Приложение 2.

При реализации второго этапа будем использовать MS Excel 2003 см. Приложение 3. При реализации третьего этапа будем использовать Мастер диаграмм в MS Excel 2003.

Последний этап представлен в Приложении 4.

ЗАКЛЮЧЕНИЕ

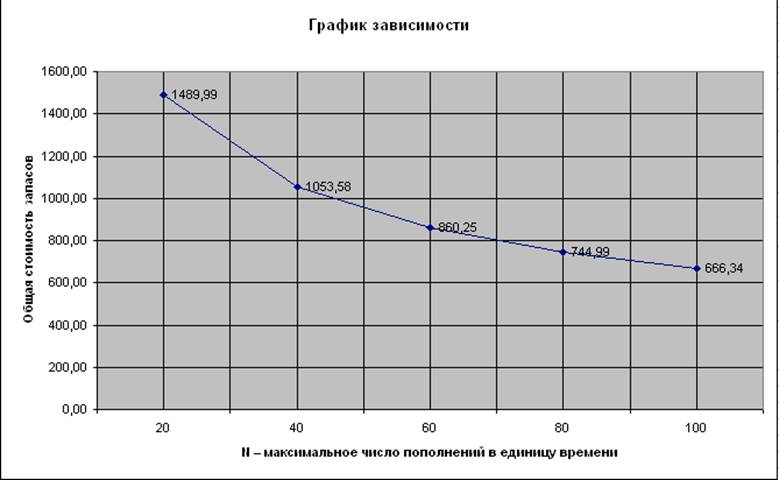
Поставленная задача осуществлена, и данный алгоритм может быть использован для решения типичных задач. Исходя из решения задачи, можно сделать вывод о том, что наиболее эффективным числом снижения стоимости запасов является 40 пополнений в год.

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1. Александрович В.М. Управление запасами и планирование снабжения: Учебное пособие по курсу «Управление запасами и планирование снабжения» для студентов специальностей «Прикладная информатика в экономике» - 080801. Алт. гос. техн. ун-т им. И. И. Ползунова. – БТИ. – Бийск. Изд-во Алт. гос. техн. ун-та, 2008.
2. Линдерс Майкл Р., Фирон Харольд Е. Управление снабжением и запасами. Логистика. Изд-во: Виктория плюс, 2006 – 768 стр.
3. Джон Шрайбфедер Эффективное управление запасами. Изд-во: Альпина Бизнес Букс, 2006 – 304 стр.

Приложения

ПРИЛОЖЕНИЕ 1

SQL – запрос на создание таблицы Wodka

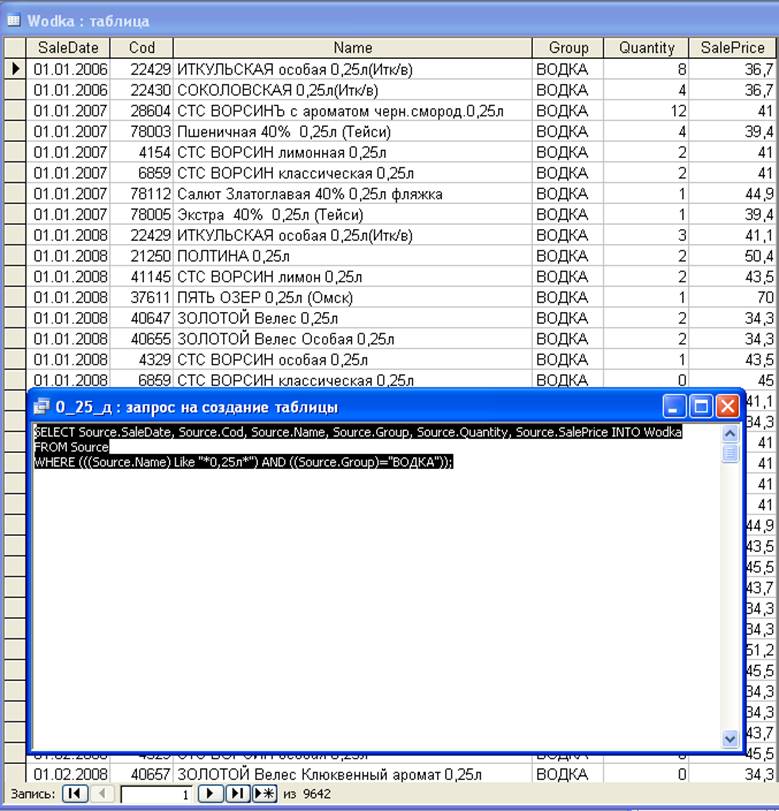
ПРИЛОЖЕНИЕ 2

Один из SQL – запроса на создание таблицы определенного вида водки

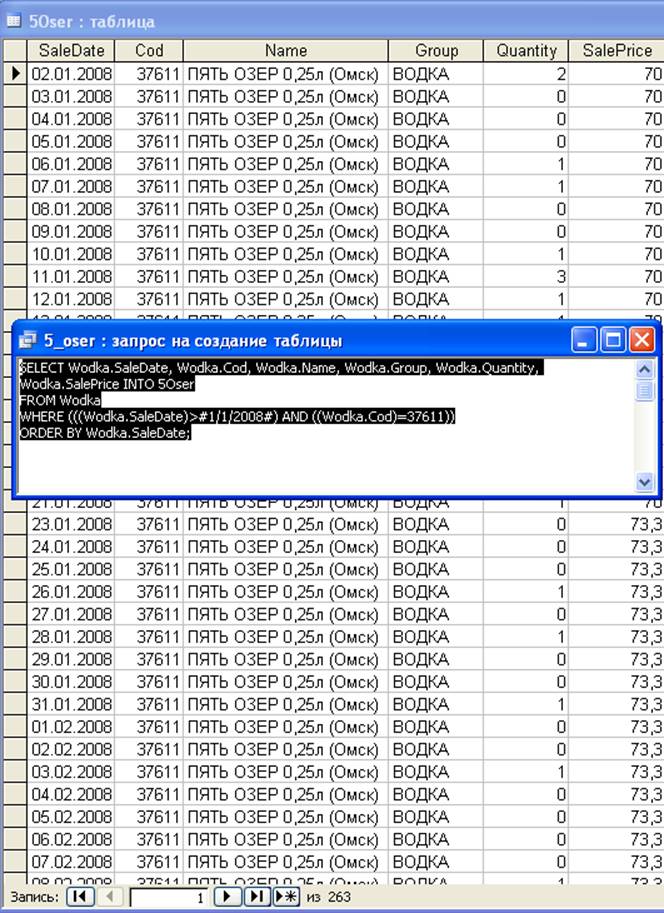
ПРИЛОЖЕНИЕ 3

Расчёты по исходным данным

ПРИЛОЖЕНИЕ 4

График зависимости C(N)