











МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ
ЛАБОРАТОРНЫХ РАБОТ ПО ДИСЦИПЛИНЕ
«КОМПЬЮТЕРНЫЕ ТЕХНОЛОГИИ В НАУКЕ
И В ПРОИЗВОДСТВЕ ЭЛЕКТРОННЫХ СРЕДСТВ»
Лабораторная работа №1
Знакомство с САПР MAX + PlusII на уровне моделирования простейших логических элементов
Цель работы:
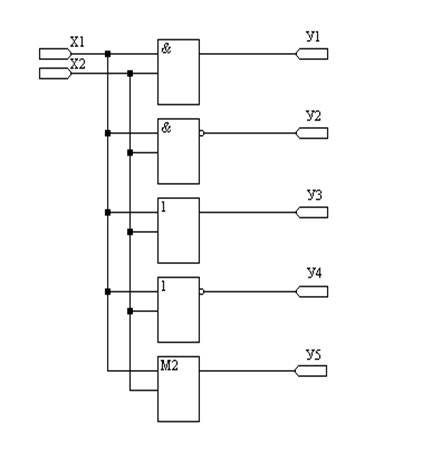
1. Ввести заданные элементы с входными и выходными контактами (2И, 2И-НЕ, 2ИЛИ, 2ИЛИ-НЕ, М2).
2. Выполнить моделирование с получением временных диаграмм
1. Условное графическое обозначение (УГО) логических элементов с входами и выходами.
2. Полученные временные диаграммы и другие способы задания логической функции (аналитический, таблица истинности) для каждого элемента. Вывод об идентичности способов задания функций.
Цель работы:
1. Умение формализовать задачу на основе словесного задания;
2. Закрепление навыков работы с САПР ALTERAMAX +PLUSII;
3. Закрепление навыков работы в графическом редакторе и функционального моделирования на уровне временных диаграмм.
1. В соответствии с условиями задачи и вариантом, заданным преподавателем:
1.1. Составить таблицу истинности функций выходов заданной схемы.
1.2. Записать аналитические выражения функций выходов.
1.3. Разработать логическую схему и ввести ее.
1.4. Построить временные диаграммы работы схемы.
1.5. Сделать выводы о работоспособности схемы.
Схема имеет 3 входа и 3 выхода.
На входы схемы одновременно поступает двоичный код.
Если число единиц во входном коде равно нулю, то на всех выходах – “0”.
Если число единиц в коде равно одной, то на первом выходе – “1”, а на остальных выходах – “0”.
Если число единиц в коде равно двум, то на втором выходе – “1”, а на остальных выходах – “0”.
Если число единиц в коде равно трем, то на третьем выходе – “1”, а на остальных выходах – “0”.
Схема имеет 3 входа и 4 выхода.
На первом выходе действует “1” только, если появился “0” на первом входе, и действует “0”, если на первом входе появилась “1”.
На втором выходе действует “1” только, если на первом входе – “1”, а на втором входе – “0”.
На третьем выходе действует код такой же, как и на третьем входе.
На четвертом выходе действует код, равный сумме по модулю 2 первого, второго и третьего выходов.
Схема имеет 3 входа и 3 выхода.
Код на первом выходе равен обратному коду, поступающему на первый вход.
Если на первый вход поступает “0” , то код на втором выходе равен коду второго входа, а код на третьем выходе равен коду третьего входа. Если на первый вход поступает “1”, то на втором выходе действует обратный код второго входа, а на третьем выходе – обратный код третьего входа.
Схема имеет 3 входа и 3 выхода.
Если во входном коде содержится нечетное число единиц, то на первом выходе действует “1”.
Если во входном коде содержится четное число единиц (или все нули), то на втором выходе действует “1”.
Если во входном коде количество единиц больше или равно двум, то на третьем выходе действует “1”.
Схема имеет 3 входа и 3 выхода.
Если на всех входах действует “0”, то и на всех выходах – “0”.
Если число единиц во входном коде больше или равно единице, то на первом выходе действует “1”.
Если число единиц во входном коде больше или равно двум, то на втором выходе действует “1”.
Если число единиц во входном коде равно трем, то на третьем выходе “1”.
Схема имеет 3 входа и 4 выхода.
На первом выходе действует “1” только, если появилась “1” на первом входе, и действует “0”, если на первом входе появился “0”.
На втором выходе действует “1” только, если на первом входе – “0”, а на втором входе – “1”.
На третьем выходе действует “1” только, если на первом и втором входах “0”, а на третьем входе – “1”.
На четвертом выходе действует код, равный сумме по модулю 2 кодов первого, второго и третьего входов.
Схема имеет 3 входа и 3 выхода.
Если на входы схемы приходит код, содержащий четное число единиц или все нули, то на первом выходе действует “1”, а на втором выходе действует “0”.
Если входной код содержит нечетное число единиц, то на втором выходе действует “1”, а на первом выходе действует “0”.
На третьем выходе действует код, равный сумме по модулю 2 кодов первого и второго входов.
Схема имеет 3 входа и 3 выхода.
Если на третьем входе действует “0”, тот код первого входа действует на первом выходе, а код второго входа – на втором выходе.
Если на третьем входе действует “1”, то на первом выходе действует обратный код первого входа, а на втором выходе – обратный код второго входа.
Код, образующийся на третьем выходе, равен сумме по модулю 2 кодов первого и второго выходов.
Схема имеет 3 входа и 3 выхода.
На первом выходе появится “1”, если равны коды на первом и втором входах, и появится “0”, если на первом и втором входах коды не равны.
На втором выходе появится “1”, если равны коды на втором и третьем входах, и появится “0”, если на втором и третьем входах коды не равны.
На третьем выходе появится “1”, если равны коды на первом и третьем входах, и появится “0”, если на первом и третьем входах коды не равны.
Схема имеет 3 входа и 4 выхода.
На первом выходе действует “1” только, если появился “0” на первом входе, и действует “0”, если на первом входе появилась”1”.
На втором выходе действует “1” только, если на первом входе “1”, а на втором входе – “0”.
На третьем выходе действует код такой же, как и на третьем входе.
На четвертом выходе действует код, равный сумме по модулю 2 первого, второго и третьего выходов.
Содержание отчета:
1. Условие задачи;
2. Таблица истинности функций выходов заданной схемы, аналитическое выражение функций выходов;
3. Логическая схема, реализующая условие задачи;
4. Временные диаграммы работы схемы;
Выводы.Лабораторная работа №3
Моделирование сумматора
Цель работы:
1. Закрепление теоретических знаний о работе сумматора;
2. Закрепление теоретических знаний о сложении двоичных чисел.
3. Закрепление навыков функционального моделирования в САПР ALTERA MAX + PLUS II.
Заполнить таблицу истинности, реализовать схему включения, получить временные диаграммы, сделать вывод.
|
Аi |
Bi |
Pi |
Si |
Pi+1 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.