Физика: Курс лекций (Понятие о векторах и простейших действиях над ними. Кинематические характеристики движения материальной точки. Кинематика гармонических колебаний)

Второй основополагающей характеристикой движения является понятие массы. Оно, так же, как и остальные величины в физике, вводится для описания наблюдаемых явлений. Все хорошо знают, что при одинаковых условиях два разных тела получают разные ускорения: при одном и том же толчке большее ускорение получат пустые санки, нежели нагруженные. Иначе говоря, тяжёлые санки более инертны, менее восприимчивы к движению, чем лёгкие. Их и остановить труднее.

Если назвать характеристику инертности тела инертной массой и обозначить её через m_и, можно удостовериться специально проведённым опытом, что ускорение обратно пропорционально массе:

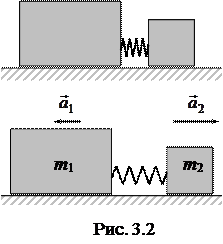Действительно, если два разных тела, соединённых упругой связью (рис. 3.2), отпустить, они получат разные ускорения, которые легко рассчитать по приведённому выше уравнению.

Обозначим свойство тел притягиваться к Земле через m_т, и назовём его тяготеющей массой. Две массы одного и того же тела (m_т и m_и) вводятся для характеристики свойств тел, проявляющихся по-разному в различных опытах. Нетрудно показать, что масса инертная и масса тяготеющая  равны друг другу. Обозначим постоянную величину в (3.3), равную произведению массы на ускорение, через F. Это не противоречит опыту (см. рис. 3.2), поскольку одинаковой для обоих взаимодействующих тел была именно сила. Тогда обратная пропорциональность массы и ускорения запишется так:

что означает: в результате действия силы величиной F на тело массы m_и, тело получило ускорение величиной а.

можно провести ещё один опыт, не связанный с первым: положим поочерёдно тела m₁ и m₂ на весы. Показания весов будут характеризовать свойство каждого из тел притягиваться к Земле, и это притяжение будет для второго тела не таким, как для первого. Используя уравнение для описания взаимодействия тела с Землей при его свободном падении, и учитывая, что тело движется с  ускорением g, будем иметь:

Эта же сила взаимодействия тела и Земли может быть также найдена по закону всемирного тяготения (3.2), в который тоже войдет масса тела, но уже иная — тяготеющая, поскольку в законе не говорится об ускорении. Приравняв правые части обсуждаемых равенств, получим:

Предполагая, что

получаем

Результат удивителен тем, что из него следует очень важный вывод: ускорение свободного падения для всех тел, находящихся на данной планете одинаково. Этот факт проверен ещё Галилеем, и хорошо известен. Из постоянства g следует справедливость гипотезы о равенстве масс инертной и тяготеющей. И в настоящее время продолжают проверять эту гипотезу, измеряя  ускорение свободного падения разных тел более точными методами.

Заметим попутно, что известная нам величина ускорения свободного падения 9,8 м/с², является такой лишь вблизи поверхности Земли, где r можно принять за радиус Земли. При увеличении расстояния от Земли ускорение свободного падения, естественно, уменьшается, но остаётся одинаковым для тел разной массы.

3.2. Второй закон Ньютона. Условия возникновения движения.

Закон инерции

Второй закон Ньютона называют основным законом динамики. Он, как и всё, о чём говорилось выше, есть обобщение наблюдений и опытов. Вместе с тем, этот закон, по определению А. Эйнштейна, есть первая ступень абстракции в физике, фактически её начало. Дело в том, что, наблюдая за окружающими нас явлениями, мы убеждаемся, что любое движение связано с силой: поезд движется до тех пор, пока работает его двигатель. Не будет силы, не будет и движения. Эти заключения верны лишь в тех условиях, которые наблюдаются на Земле, то есть при наличии трения.

Если представить, что силы трения исчезли, то движение представится нам возможным и без действия силы: шайба, брошенная по льду, будет скользить по нему бесконечно долго, тем дольше, чем меньше трение. Планеты и другие небесные тела движутся, не теряя своей скорости, потому что их движению практически ничего не мешает. В число небесных тел мы теперь можем включить и искусственные