Руководство к решению задач по электростатике: Учебное пособие для самостоятельной работы студентов

Министерство образования и науки Российской Федерации

Южно-Уральский государственный университет

Филиал в г. Златоусте

Кафедра физики № 3

537(07)     

Е702               

,

Руководство к решению задач по электростатике

Учебное пособие для самостоятельной работы студентов

Челябинск

Издательский центр ЮУрГУ

2011

ВВЕДЕНИЕ

Данное пособие предлагается студентам инженерных специальностей и технических направлений подготовки бакалавров для самостоятельного овладения навыками решения задач по электростатике. В пособии приводится набор типовых задач по четырем разделам электростатики: от взаимодействия точечных зарядов до задач на движение заряженных частиц в электростатическом поле, рассматриваются примеры подробного решения. Задачи могут использоваться в качестве индивидуальных домашних заданий и заданий на контрольной работе.

При самостоятельной работе с пособием студентам рекомендуется обязательно просматривать примеры подробного решения задач, переписывать эти образцы в рабочую тетрадь и пробовать решить другие задачи раздела по предложенному образцу. Оформление рисунков и чертежей требует отдельного внимания, так как это влияет на правильность решения задач.

Требования к оформлению задач:

·  после записи номера задачи полностью переписывается ее условие;

·  вводятся обозначения («Дано:», «Найти:»);

·  выполняется пояснительный рисунок, на котором должны быть отмечены все объекты, упоминаемые в условии и в решении задачи (в редких случаях рисунок не требуется);

·  все используемые в решении задачи законы и формулы приводятся полностью, расчетные формулы подробно выводятся, после каждой математической выкладки должно быть дано исчерпывающее пояснение;

·  задача решается в общем виде, т.е. выводится конечная расчетная формула, в которую входят только известные величины (промежуточные вычисления допускаются только в том случае, когда решение задачи громоздко);

·  по расчетным формулам проверяются размерности искомых величин;

·  единицы физических величин должны соответствовать системе единиц СИ;

·  расчёты выполняются с той точностью, с которой заданы исходные данные (обычно две – три значащих цифры);

·  записывается полный ответ на все вопросы задачи.

Задачи для самостоятельного решения выполняются и сдаются на проверку по мере изучения материала либо в сроки, указанные преподавателем. Выполнение домашних контрольных работ входит в обязательный учебный график СРС по физике.

Перед решением задач необходимо повторить теоретический материал, соответствующий разделу. Для изучения и повторения теоретического материала студентам предлагается пользоваться учебниками по физике [1, 2]. Также рекомендуются другие пособия, предлагающие разбор задач по данным разделам курса физики.

1. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ ТОЧЕЧНОГО ЗАРЯДА

Пример 1.1

Условие

В четырех вершинах квадрата со стороной 0,5 м находятся четыре одинаковых по модулю заряда 3∙10^–9Кл каждый. Заряды Q₁ и Q₂ отрицательные, а Q₃ и Q₄ – положительные (рис. 1.1).

Найти:

1)  напряженность и потенциал электрического поля системы зарядов в точке A и силу, действующую на электрон и протон в этой точке;

2)  работу по перемещению протона из точки A в точку B в электростатическом поле системы зарядов.

 

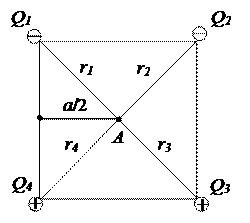Дано:                      

Q₁ = –3∙10^–9 Кл

Q₂ = –3∙10^–9 Кл

Q₃ = 3∙10^–9 Кл

Q₄ = 3∙10^–9 Кл

a = 0,5 м

 

E – ?; F – ?; A – ?;

φ – ?

                                    Рис. 1.1

Решение

Если электростатическое поле создано системой электрических зарядов, то результирующие напряженность и потенциал в любой точке этого поля находятся по принципу суперпозиции: Е

                                            (1.1)

                                     (1.2)

Найдем результирующую напряженность в точке A. В данной задаче четыре точечных заряда, следовательно,

                                             (1.3)

Изобразим эти векторы в точке A (рис. 1.2). Напряженность поля точечного заряда находится по формуле

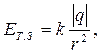                                                               (1.4)

где k – коэффициент пропорциональности в системе СИ,

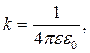                                                                  (1.5)

½q½– модуль заряда, создающего электрическое поле, r – расстояние от заряда до точки, в которой определяется напряженность; ε – диэлектрическая проницаемость среды; ε = 1 для воздуха и вакуума, ε₀ = 8,85∙10^–12 Ф/м – электрическая постоянная.

Рис. 1.2

По условию

½q₁½=½q₂½=½q₃½=½q₄½,                                           (1.6)

а также

r₁ = r₂ = r₃ = r₄ ,                                                 (1.7)

так как заряды находятся в вершинах квадрата, а точка А – в его центре. Из рис. 1.1 по теореме Пифагора

r₁ = r₂ = r₃ = r₄=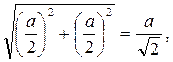

где а – сторона квадрата. Из (1.4), (1.6) и (1.7) следует, что  – модули векторов напряженности. Найдем геометрическую сумму векторов (рис. 1.3):

 

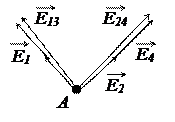                                            (1.8)

                           Рис. 1.3

Векторы  попарно со направлены отсюда скалярный вид данных выражений:

 

    → .                                       (1.9)

Результирующий вектор напряженности в точке А:  (рис. 1.4).

Модуль вектора  найдем по теореме Пифагора, так как  перпендикулярен  (эти векторы направлены по диагоналям квадрата),

                                        (1.10)

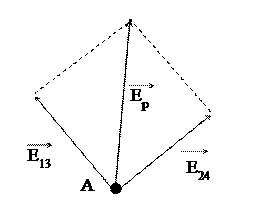
Рис. 1.4

С учетом (1.9)

                                                               (1.11)

с учетом (1.4) и (1.8) модуль результирующего вектора напряженности в точке A

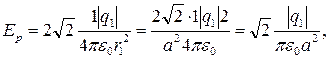
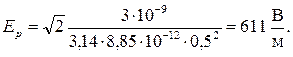
Найдем результирующий потенциал в точке А:

                                      (1.12)

Потенциал поля точечного заряда

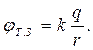                                                         (1.13)

Тогда результирующий потенциал A с учетом (1.8) и (1.13)

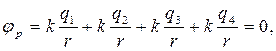                               (1.14)

так как j₁ = j₂  < 0, а j₃ = j₄  > 0.

Найдем силу, действующую на протон и электрон в точке A:

F_эл  = Eq.                                                    (1.15)

Это электрическая сила, действующая со стороны электростатического поля на заряд, помещенный в это поле.

Тогда сила, действующая на протон

F_п  = E_рq_п,      (1.16)

сила, действующая на электрон

F_е  = E_рq_е,       (1.17)

½q_п½=½q_е½, но q_п > 0, а q_е < 0 → , но направление сил противоположно друг другу (рис. 1.5):

 = 611∙1,6∙10^–19  ≈  978∙10^–19  Н.

∙

	Рис. 1.5

 

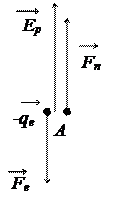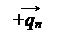
Найдем работу по перемещению протона из точки А в точку В:

А = – qΔj = q(j₁ – j₂).                                   (1.18)

Для нашей задачи

А = – q_п(j_А – j_В).                                 (1.19)

Результирующий потенциал в точке А найден и равен 0.

Найдем результирующий потенциал в точке В:

– по признаку суперпозиции.

Из рис. 1.1

      → j₁ + j₄= 0;

Q₄ = – Q₁.

Из рис. 1.6

r₂ = r₃

Q₄ = – Q₁.      → j₂ + j₃= 0.

Таким образом результирующий потенциал в точке В

= 0.

Следовательно А = q_п(j_А + j_В) = 0.

Ответ:  Е_р  = 611 В/м;  j_р  = 0;  ½F_п½  = ½E_е½ = 978 10^–19  Н; А = 0.

 

Рис. 1.6

Пример 1.2

Условие

В четырех вершинах правильного шестиугольника со стороной